系列文章目录
《信号类型(通信)——仿真》
《信号类型(通信)——QAM调制信号》
文章目录
前言
一、QPSK通信调制信号
1.1、原理
1.2、仿真
二、OQPSK通信调制信号
1.1、原理
1.2、仿真
三、IJF_OQPSK通信调制信号
1.1、原理
1.2、仿真
总结
前言
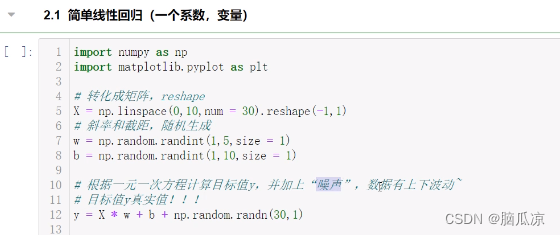
前面介绍了QAM调制信号,M=4是,QAM可以认为是QPSK调制。本文主要介绍QPSK、OQPSK、IJF_OQPSK调制解调过程。
一、QPSK通信调制信号
1.1、原理
在数字信号的调制方式中QPSK四相移键控是目前最常用的一种卫星数字信号调制方式,它具有较高的频谱利用率、较强的抗干扰性、在电路上实现也较为简单。

QPSK信号调制的原理框图
QPSK信号产生过程:基带码元波形经过QPSK映射(串并转换分成I、Q两路,然后再经过电平转换,0转换成1,1转换-1)得到QPSK调制信号,再与对应的载波相乘,然后再相加完成QPSK的调制。
其中,
,
为载频,
为QPSK调制码的IQ表示,
为码宽,
为码波形,由成型滤波器决定。
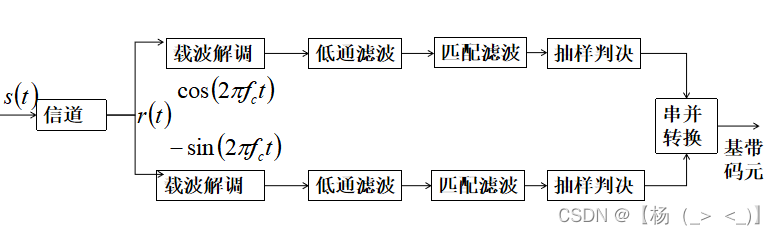
QPSK信号解调的原理框图
QPSK信号再分为I、Q两路和对应的载波相乘,然后经过低通滤波器得到基带信号:
其中,
表示接收机噪声,
分别表示IQ路噪声。
对下变频后的基带信号进行匹配滤波,并进行抽样判决,恢复出原始的码元序列。
1.2、仿真
参数设置,符号速率60kHz,采样率12 Mz,载频 1.5MHz,码序列随机生成,成型滤波器采用根升余弦滤波器,滚降系数决定码波形。信噪比10dB。

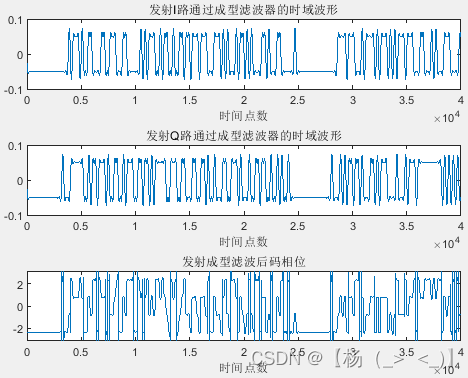
码序列 成型滤波后基带信号
帧信号由帧头,帧体和帧尾构成,帧头和帧尾固定,帧体数据随机生成,生成的码序列如左上图所示。成型滤波器滚降系数0.8,码长6,对码脉冲信号进行成型滤波,得到右上图所示的基带信号,可以看出经过成型滤波处理,码宽内的相位不再是固定值。最后载频调制得到最终发射信号,如下图所示。

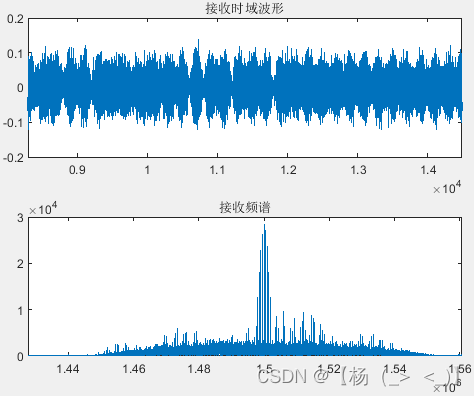
发射的射频信号波形以及频谱
只考虑接收机的热噪声影响,得到如上图所示接收信号。与发射信号相比,信号波形存在随机波动。对接收的信号进行下变频至基带得到左下1图的基带信号,通过对信号进行截断得到左下2图所示的眼图,并基于最佳点得到左下3图所示的眼图。


下变频后基带信号的波形,眼图以及基于最佳点的星座图
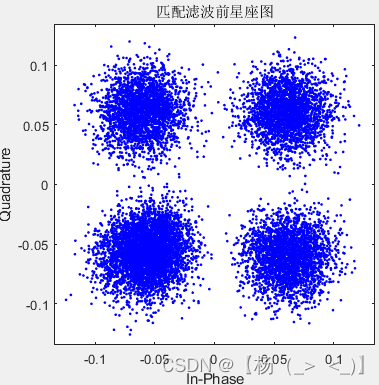
对下变频后的基带信号进行匹配滤波得到左下1图的基带信号,通过对信号进行截断得到左下2图所示的眼图,并基于最佳点得到左下3图所示的眼图。与匹配滤波前相比,信号的眼图以及星座图得到明显改善。


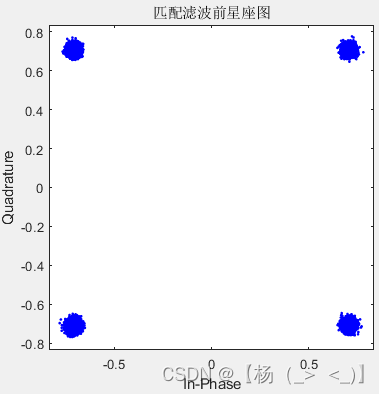
匹配滤波后基带信号的波形,眼图以及基于最佳点的星座图
二、OQPSK通信调制信号
1.1、原理
与QPSK相比,OQPSk调制方式在复数通道Q通道中,插入了一个比特的时延。因此OQPSK调制信号为:
其中,
,
为载频,
为QPSK调制码的IQ表示,
为码宽,
为码波形,由成型滤波器决定。
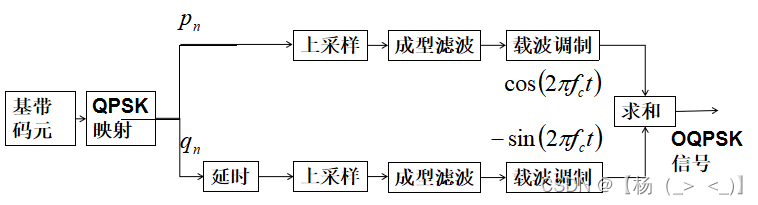 OQPSK信号调制的原理框图
OQPSK信号调制的原理框图
QPSK信号再分为I、Q两路和对应的载波相乘,然后经过低通滤波器得到基带信号:
其中,
表示接收机噪声,
分别表示IQ路噪声。
对下变频后的基带信号进行匹配滤波,并进行抽样判决,恢复出原始的码元序列。因为调制时Q路进行了延时,所以解调时I路也进行相同的延时。

OQPSK信号解调的原理框图
1.2、仿真


码序列 成型滤波后基带信号
帧信号由帧头,帧体和帧尾构成,帧头和帧尾固定,帧体数据随机生成,生成的码序列如左上图所示。成型滤波器滚降系数0.8,码长6,对码脉冲信号进行成型滤波,得到右上图所示的基带信号,可以看出经过成型滤波处理,码宽内的相位不再是固定值。最后载频调制得到最终发射信号,如下图所示,可以看出信号包络不过零。
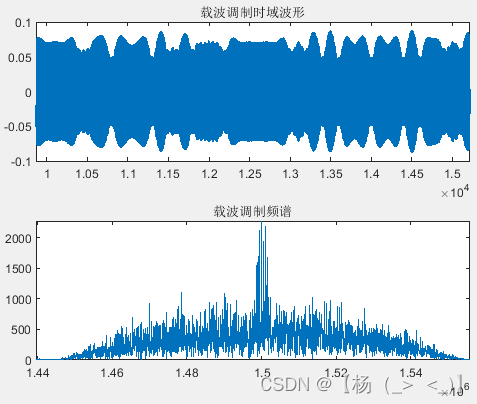
发射的射频信号波形以及频谱
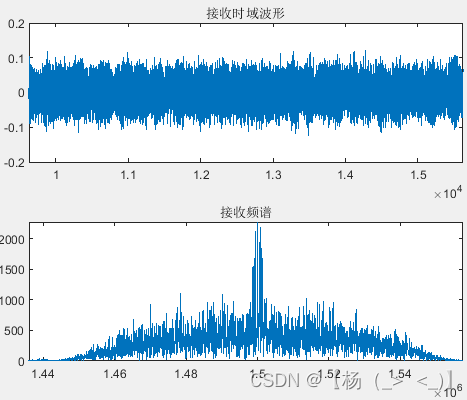
只考虑接收机的热噪声影响,得到如上图所示接收信号。与发射信号相比,信号波形存在随机波动。对接收的信号进行下变频至基带,然后对下变频后的基带信号进行匹配滤波得到左下1图的基带信号,通过对信号进行截断得到左下2图所示的I路眼图,左下3图所示的Q路眼图,可以发现IQ两路存在明显错位。



匹配滤波后基带信号的波形,I路眼图以及Q路眼图
三、IJF_OQPSK通信调制信号
1.1、原理
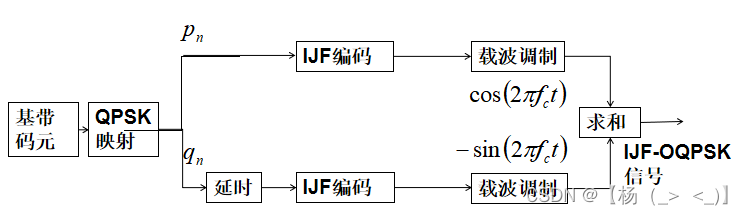
IJF_OQPSK信号调制的原理框图
与OQPSK相比,IJF——OQPSk调制方式通过IJF编码进行波形设计。IJF编码规则如下:
其中
,
因为调制时Q路进行了延时,所以解调时I路也进行相同的延时。
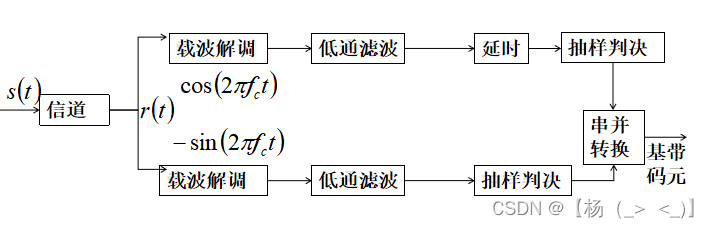
IJF_OQPSK信号解调的原理框图
1.2、仿真

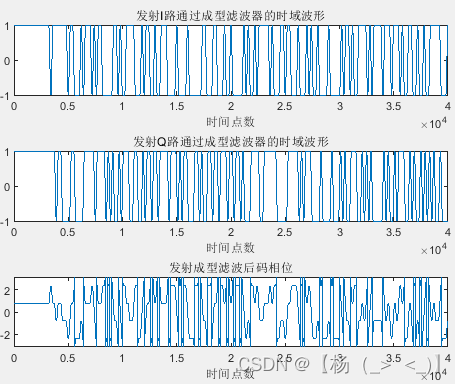
码序列 成型滤波后基带信号
帧信号由帧头,帧体和帧尾构成,帧头和帧尾固定,帧体数据随机生成,生成的码序列如左上图所示。经过IJF编码得到右上图所示的基带信号,可以看出码宽内的相位不再是固定值。最后载频调制得到最终发射信号,如下图所示,可以看出信号包络不过零。


发射的射频信号波形以及频谱
只考虑接收机的热噪声影响,得到如上图所示接收信号。与发射信号相比,信号波形存在随机波动。对接收的信号进行下变频至基带,然后对下变频后的基带信号进行匹配滤波得到左下1图的基带信号,通过对信号进行截断得到左下2图所示的I路眼图,左下3图所示的Q路眼图,可以发现IQ两路存在明显错位。

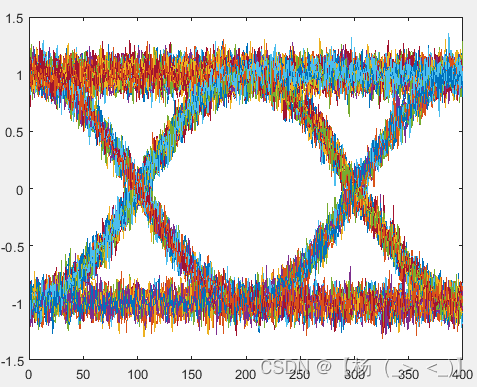
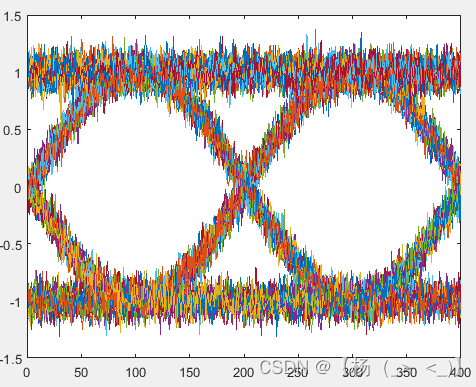
匹配滤波后基带信号的波形,I路眼图以及Q路眼图
总结
本文主要从仿真的角度简单分析了QPSK、OQPSK以及IJF_OQPSK调制解调过程,实际环境中的多普勒效应以及多径效应等并没有考虑。有更好的内容欢迎在评论区放置链接,另外有问题也欢迎评论区留言。转载请附链接【杨(_> <_)】的博客_CSDN博客-信号处理,SAR,代码实现领域博主。