AcWing 1497：树的遍历-编程知识

AcWing 1497：树的遍历

【题目来源】
https://pintia.cn/problem-sets/994805342720868352/exam/problems/994805485033603072
https://www.acwing.com/problem/content/description/1499/

【题目描述】
一个二叉树，树中每个节点的权值互不相同。
现在给出它的后序遍历和中序遍历，请你输出它的层序遍历。

【输入格式】
第一行包含整数 N，表示二叉树的节点数。
第二行包含 N 个整数，表示二叉树的后序遍历。
第三行包含 N 个整数，表示二叉树的中序遍历。

【输出格式】
输出一行 N 个整数，表示二叉树的层序遍历。

【数据范围】
1≤N≤30，
官方并未给出各节点权值的取值范围，为方便起见，在本网站范围取为 1∼N。

【输入样例】
7
2 3 1 5 7 6 4
1 2 3 4 5 6 7

【输出样例】
4 1 6 3 5 7 2

【算法分析】
◆● unordered_map
https://cplusplus.com/reference/unordered_map/
（1）unordered_map 适用于需要快速查找，且不要求元素存储顺序的场景，尤其适合使用自定义类型作为键的情况。但是需要注意的是，unordered_map 并不支持 lower_bound 和 upper_bound 等操作。因此，在需要按照键值的大小顺序查找元素时，可以考虑使用 map。
（2）从 C++ 11 开始，hash_map 实现已被添加到 C++ STL 标准库中，但为了防止与已有的代码存在冲突，决定使用替代名称 unordered_map。这个名字其实更具描述性，因为说明了该类元素的无序性。当然，这也决定了若要使用unordered_map，必须使用支持C++ 11标准的编译器。
在Dev-C++中可按下图所示进行设置，使之支持C++ 11。

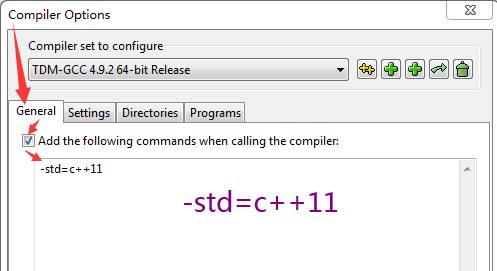
（3）unordered_map内部实现了一个哈希表（也叫散列表，通过把关键码值映射到Hash表中一个位置来访问记录，查找的时间复杂度可达到O(1)，故其在海量数据处理中有着广泛应用）。

◆● unordered_map::count
https://cplusplus.com/reference/unordered_map/unordered_map/count/

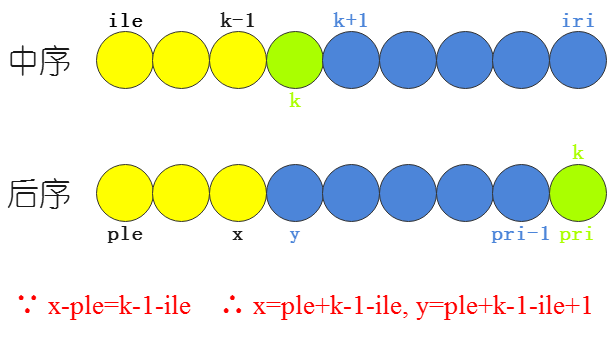
◆● 二叉树构建函数的参数确立示意图
ile：中序遍历左端点位置，iri：中序遍历右端点位置
ple：后序遍历左端点位置，pri：后序遍历右端点位置

【算法代码】

#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#include <queue>
using namespace std;const int maxn=35;
int n;
int postorder[maxn],inorder[maxn];
unordered_map<int,int> le,ri,pos;int build(int ile,int iri,int ple,int pri){int root=postorder[pri];int k=pos[root];if(ile<k) le[root]=build(ile,k-1,ple,ple+k-1-ile);if(iri>k) ri[root]=build(k+1,iri,ple+k-1-ile+1,pri-1);return root;
}void bfs(int root){queue<int> q;q.push(root);while(!q.empty()){ //q.size()int t=q.front();q.pop();cout<<t<<" ";if(le.count(t)) q.push(le[t]);if(ri.count(t)) q.push(ri[t]);}
}int main(){cin>>n;for(int i=0;i<n;i++) cin>>postorder[i];for(int i=0;i<n;i++){cin>>inorder[i];pos[inorder[i]]=i;}int root=build(0,n-1,0,n-1);bfs(root);return 0;
}/*
in:
7
2 3 1 5 7 6 4
1 2 3 4 5 6 7out:
4 1 6 3 5 7 2
*/

【参考文献】
https://blog.csdn.net/Jacksqh/article/details/111188208
https://www.acwing.com/video/2647/
https://blog.csdn.net/ly0724ok/article/details/117362251
https://blog.csdn.net/lzq8090/article/details/129788666