一、应用情境

输入任意长度个向量进行处理。

从输入看

• 文字处理（自然语言处理）
  • 将word表示为向量
    • one-hot
    • word-embedding
• 声音信号处理
  • 每个时间窗口（Window, 25ms）视为帧（Frame）,视为向量
• 图
  • 每个节点视为一个向量
    • Social graph（社交网络图）
    • 分子式【one-hot】

从输出看

• √ 输入输出数量相等【每个向量都有一个标签】⇒sequence Labeling
  • 词性标注（POS tagging）
  • 语音辨识（每个vector对应phoneme）
  • 社交网络（每个节点（人）进行标注【是否推送商品】）
• 整个输入序列只有一个输出
  • 文本情感分析
  • 语者辨认
  • 分子的疏水性
• 由模型决定输出的数目【seq2seq】
  • 翻译
  • 语音辨识

 

二、Sequence Labeling

• 对每一个向量，用Fully-connected network分别进行处理
  • 问题：忽略了序列上下文的关系
    • 同一个向量在序列号中不同的位置、不同的上下文环境下，得到的输出可能不同（需要考虑序列）
  • 改进：串联若干个向量
    • 问题：
      • 只能考虑固定个，不能考虑”任意长度“
      • 网络参数大

三、Self-attention

特点：考虑整个序列sequence的所有向量，综合向量序列整体和单个向量个体，得到对每一个向量处理后的向量

⇒将这个向量链接一个FC，FC可以专注于处理这一个位置的向量，得到对应结果。

其中，self-attention 的功能是处理整个 sequence 的信息，而 FC 则是处理某一个位置的信息，

Self-attention+FC可以交替使用

知名文章：Attention is all you need ⇒Transformer

基本原理

输入：一串的 Vector，这个 Vector 可能是整个 Network 的 Input，也可能是某个 Hidden Layer 的 Output

输出：处理 Input 以后，每一个 bi 都是考虑了所有的 ai 以后才生成出来的

具体步骤如下：

1. 以 a1 为例，根据 a1 这个向量，找出整个 sequence 中跟 a1 相关的其他向量 ⇒ 计算哪些部分是重要的，求出 ai 和 a1 的相关性（影响程度大的就多考虑点），用 α 表示

2. 计算相关性：有 点积 和 additive 两种方法计算相关性。

✔️方法一 dot product：

输入的这两个向量分别乘上两个不同的矩阵,左边这个向量乘上矩阵 W^q得到矩阵 q,右边这个向量乘上矩阵 W^k得到矩阵 k;再把 q跟 k做dot product，逐元素相乘后累加得到一个 scalar就是α

方法二 Additive：

得到 q跟 k后，先串接起来,再过一个Activation Function（Normalization），再通过一个Transform,然后得到 α

需要计算：任意两个向量之间的关联性，作softmax【不一定要用，也可以用其他激活函数】，得到

把 a1 乘上 Wq 得到 q，叫做 Query（就像是搜寻相关文章的关键字，所以叫做 Query）

然后将 ai 都要乘 Wq 得到 k，叫做 Key，把这个Query q1 和 Key ki 进行 点积操作 就得到 相关性 α（ α 叫做 Attention Score，表示 Attention计算出的 vector 之间的相关性）

attention score 还要经过一层 softmax 才能用于后续处理，其中 softmax 也可以换成其他的 activation function

3. 分别抽取重要信息，根据关联性作加权求和得到  bi 

（一次性并行计算出 bi ，不需要依次先后得出）

优点：bi 是并行计算得出

矩阵的角度表示 Self-attention 计算过程

① 计算 k，q，v （其中 Wq 、Wk 和 Wv 都是要学习的网络参数矩阵）

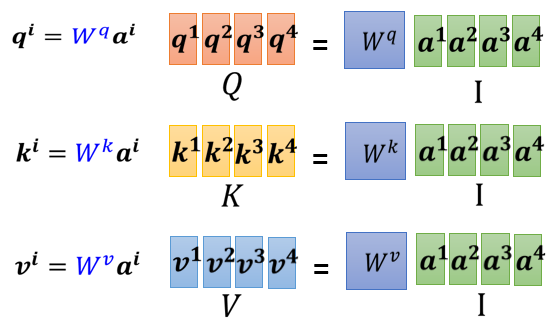
② 计算 α 并 Normalization

③ 计算 b

综合：

 其中，

• I 是 Self-attention 的 input（一排 vector），每个 vector 拼起来当作矩阵的 column
• 这个 input 分别乘上三个矩阵， 得到 Q K V
• 接下来 Q 乘上 K 的 transpose,得到 A 。可能会做一些处理,得到 A' ,叫做Attention Matrix ，生成 Q 矩阵就是为了得到 Attention 的 score
• A' 再乘上 V，就得到 O，O 就是 Self-attention 这个 layer 的输出

唯一需要学的参数：三个矩阵

四、Multi-head Self-attention

1. 特点

使用多个 q  k  v  组合，不同的 q k v 负责不同种类的相关性

例如在下图中，一共有2类， 1类的放在一起算，2类的放在一起算。相关性变多了，所以参数也增加了，原来只需要三个 W 矩阵，现在需要六个 W 矩阵

 2. 计算步骤

• 先把 a 乘上一个矩阵得到 q

• 再把 q 乘上另外两个矩阵，分别得到  q1 跟  q2，代表有两个 head；同理可以得到 k1， k2，v1， v2

• 同一个 head 里的  k  q  v 计算 b.

• 

• 将各个 head 计算得到的  bi 拼接，通过一个 transform得到 bi，然后再送到下一层去

3. Positional Encoding

每个向量所处的“位置”需要被编码

方法：每个位置用一个 vector ei 来表示它是 sequence 的第 i 个。加和到原向量中。

如何产生positional encoding vector尚待研究

• 手工设置
• 根据资料学出来

五、Applications

BERT

Self-attention for Speech

问题：

把一段声音讯号,表示成一排向量的话,这排向量可能会非常地长；attention matrix 的计算复杂度是长度的平方需要很大的计算量、很大的存储空间

方法：Truncated Self-attention

要看一整句话,只看一个小的范围就好——辨识这个位置有什麼样的phoneme只要看这句话,跟它前后一定范围之内的资讯就可以判断

Self-attention for Image

每一个 pixel就是一个三维的向量，整张图片其实就是长乘以宽个向量的set

Self-attention GAN1

六、Self-attention 和 CNN RNN GNN

1. 和CNN的对比

CNN 可以看成简化版的 self-attention，CNN 就是只计算感受域中的相关性的self-attention。

• CNN：感知域（receptive field）是人为设定的，只考虑范围内的信息
• Self-attention：考虑一个像素和整张图片的信息 ⇒ 自己学出“感知域”的形状和大小

结论：

CNN 就是 Self-attention 的特例，Self-attention 只要设定合适的参数，就可以做到跟 CNN 一模一样的事情

self attention 是更 flexible 的 CNN

⇒ self-attention需要 更多的数据 进行训练，否则会 欠拟合；否则CNN的性能更好

• Self-attention 它弹性比较大,所以需要比较多的训练资料,训练资料少的时候,就会 overfitting
• 而 CNN 它弹性比较小,在训练资料少的时候,结果比较好,但训练资料多的时候,它没有办法从更大量的训练资料得到好处

2. 和 RNN 的对比

recurrent neural network 的角色,很大一部分都可以用 Self-attention 来取代了

Recurrent Neural Network跟 Self-attention 做的事情其实也非常像,它们的 input 都是一个 vector sequence

• 左边是你的 input sequence,你有一个 memory 的 vector
• 然后你有一个 RNN 的 block,吃 memory 的 vector,吃第一个 input 的 vector
• 然后 output hidden layer 的 output
• 然后通过fully connected network,做你想要的 prediction
• 接下来当sequence 裡面第二个 vector 作為 input 的时候,也会把前一个时间点吐出来的东西,当做下一个时间点的输入,再丢进 RNN 裡面,然后再產生新的 vector,再拿去给 fully connected network

RNN 其实也可以是双向的,从而使得 memory 的 hidden output,其实也可以看作是考虑了整个 input 的 sequence

主要区别：

• 对 RNN 来说，最终的输出要考虑最左边一开始的输入 vector，意味着必须要把最左边的输入存到 memory 里面并且在计算过程中一直都不能够忘掉，一路带到最右边，才能够在最后一个时间点被考虑（依次按顺序输出）
• 对 Self-attention 可以在整个 sequence 上非常远的 vector之间轻易地抽取信息

并行输出，速度更快，效率更高：

• Self-attention：四个 vector 是平行產生的,并不需要等谁先运算完才把其他运算出来
• RNN 是没有办法平行化的，必须依次产生

很多的应用都往往把 RNN 的架构，逐渐改成 Self-attention 的架构

3. 和 GNN 的对比

Self-attention for Graph⇒一种GNN

• 在 Graph 上面，每一个 node 可以表示成一个向量
• node 之间是有相连的，每一个 edge 标志着 node 跟 node 之间的关联性
• 比如：在做Attention Matrix 计算的时候，只需计算有 edge 相连的 node
• 因為这个 Graph 往往是人為根据某些 domain knowledge 建出来的，已知这两个向量彼此之间没有关联（图矩阵中对应结点 i 与 结点 j 之间没有数值），就没有必要再用机器去学习这件事情

MORE

冷知识：有人说广义的 Transformer,指的就是 Self-attention

Self-attention 有非常非常多的变形,Self-attention 它最大的问题就是,它的运算量非常地大

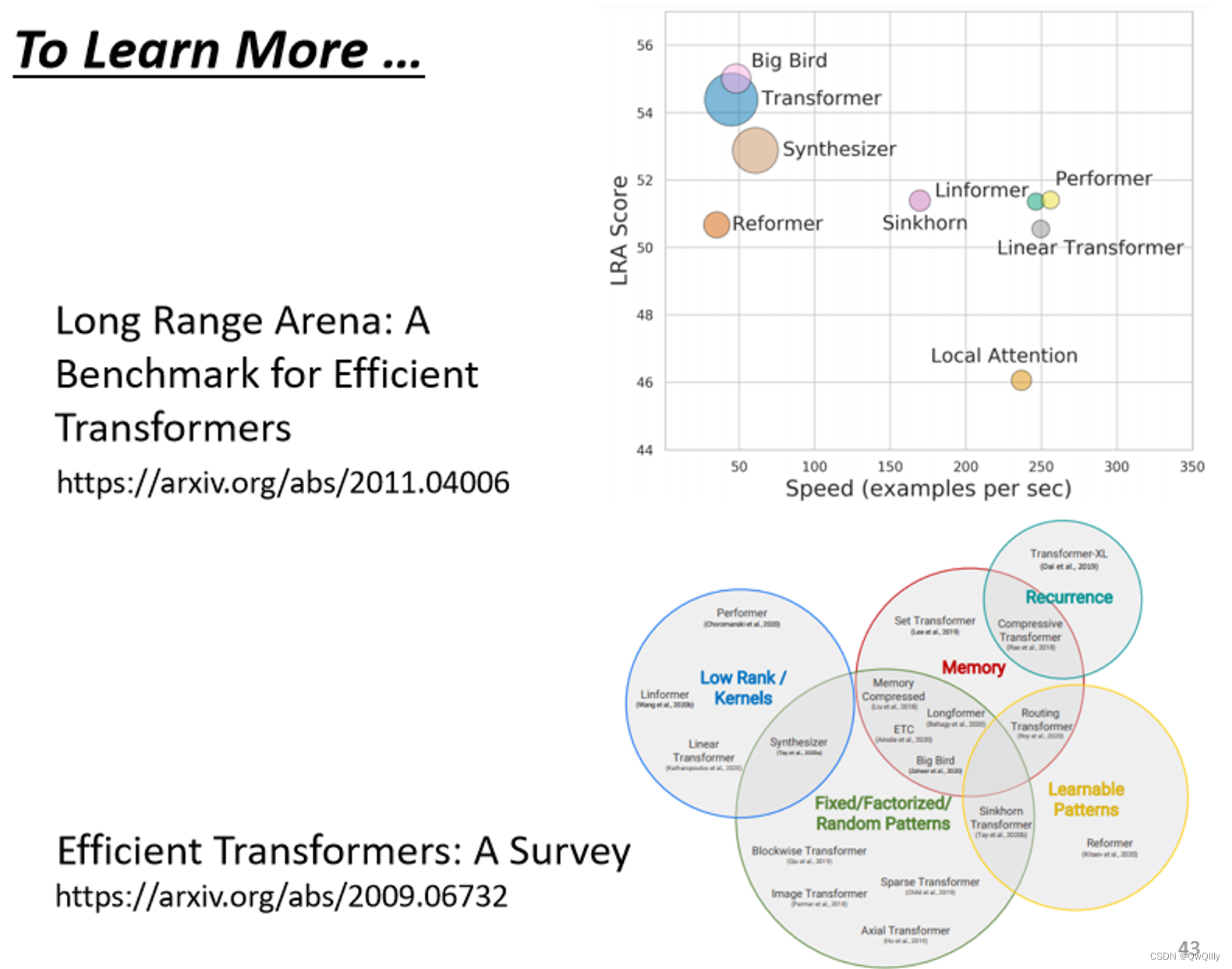
paper：Long Range Arena比较了各种不同的 Self-attention 的变形

Efficient Transformers: A Survey 这篇 paper,介绍各式各样 Self-attention 的变形