软考高级之系统架构师之计算专题-编程知识

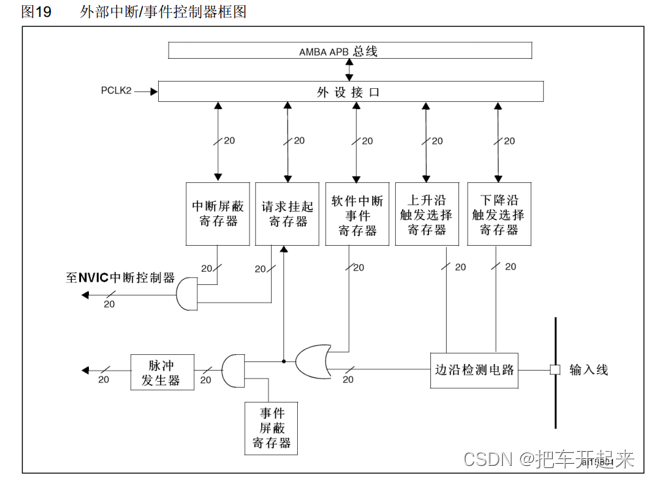
操作系统

需要一定操作系统基础知识才能计算的题目。

吞吐率

某指令流水线由5段组成，各段所需要的时间如下图所示。连续输入100条指令时的吞吐率为（）。
在这里插入图片描述
解析：
指令流水线的吞吐率定义为： $吞吐率TP=\frac{指令数}{执行时间}$ 。该流水线开始运行后，第二条指令的第一段就与第一条指令的第二段就开始重叠执行。流水线的建立时间为第一条指令的执行时间，此后每3△t就执行完一条指令，因此执行100条指令的时间为t+3t+t+2t+t+(100-1)*3t=305t，故吞吐率为 $\frac{100}{205Δt}$ 。

加速比

某计算机系统采用5级流水线结构执行指令，设每条指令的执行由取指令（2Δt）、分析指令（1Δt）、取操作数（3Δt）、运算（1Δt）和写回结果（2Δt）组成，并分别用5个子部件完成，该流水线的最大吞吐率为（）；若连续向流水线输入10条指令，则该流水线的加速比为（）。

解析：
流水线的吞吐率是指单位时间内流水线完成的任务数或输出的结果数量，其最大吞吐率为瓶颈段所需时间的倒数。瓶颈为取操作数段，故最大吞吐率为 $\frac{1}{3Δt}$ 。

流水线的加速比是指完成同样一批任务，不使用流水线（即顺序执行所有指令）所需时间与使用流水线（指令的子任务并行处理）所需时间之比。执行1条指令的时间为2Δt+1Δt+3Δt+1Δt+2Δt=9Δt，顺序执行10条指令所需时间为90Δt。若采用流水线，则所需时间为9Δt+(10-1)*3Δt=36Δt，因此加速比为90:36=5:2。

缺页中断

某虚拟存储系统采用最近最少使用（LRU）页面淘汰算法，假定系统为每个作业分配4个页面的主存空间，其中一个页面用来存放程序。现有某作业的程序如下：

Var A: Array[1..100,1..100] OF integer;i,j: integer;FOR i:=1 to 100 DOFOR j:=1 to 100 DOA[i,j]:=0;

设每个页面可存放200个整数变量，变量i、j存放在程序页中。初始时，程序及i、j均已在内存，其余3页为空。若矩阵A按行序存放，那么当程序执行完后共产生（）次缺页中断；若矩阵A按列序存放，那么当程序执行完后共产生（/）次缺页中断。

解析：
矩阵A[100][100]总共有100行、100列，若矩阵A按行序存放，则每一个页面可以存放2行，也就是说矩阵的2行刚好放在1页内，访问它们需要中断1次，这样100行总共需要中断50次。

若矩阵A按列序存放，则每一个页面可以存放2列，也就是说矩阵的2列刚好放在1页内，由于内循环FOR j:=1 to 100 DO是按列序变化，访问它们需要中断50次，这样100行总共需要中断50*100=5000次。

地址转换

假设系统采用段式存储管理方法，进程P的段表如下所示。逻辑地址（）不能转换为对应的物理地址，原因是进行（）。

段号	基地址	段长
0	1100	800
1	3310	50
2	5000	200
3	4100	580
4	2000	100

解析：
给定段地址(x,y)，其中x为段号，y为段内地址。将(x,y)转换为物理地址的方法是：根据段号查段表再判断段长。如果小于段长，则物理地址=基地址-段内地址y，否则地址越界。

具体地，段地址(0,810)中，0段的段长为800，段内地址810大于段长，故地址越界。段地址(4,120)中，4段的段长为100，段内地址120大于段长，故地址越界。

原因：逻辑地址到物理地址转换时地址越界。

数学

概率

1路和2路公交车都将在10分钟内均匀随机地到达同一车站，则它们相隔4分钟内到达该站的概率为（）。

解析：
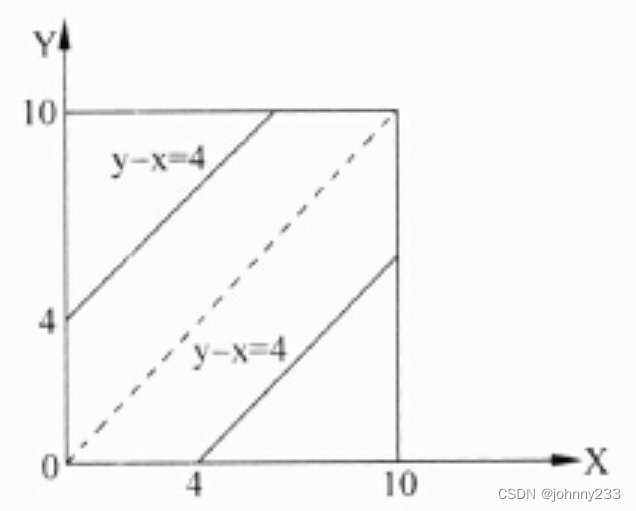
设1路和2路公交车将分别在x和y分钟内到达该站，则x和y是在[0,10]内独立均匀分布的随机变量，等价于计算||x-y|≤4的概率。
平面上的点(x,y)必然在正方形[0, 10:0, 10]内均勻分布，|x-y|≤4的概率应当等于该正方形中|x-y|≤4的部分面积的比例。该正方形的面积为100，|x-y|≤4部分的面积为64，|x-y|≤4的概率为0.64。
在这里插入图片描述

矩阵

某类产品N种品牌在某地区的市场占有率常用概率向量u=(ui, u2, …, un)表示（各分量分别表示各品牌的市场占有率，值非负，且总和为1）。市场占有率每隔一定时间的变化常用转移矩阵Pn*n表示。如果在相当长时期内，该转移矩阵的元素均是常数，又设初始时刻的市场占有率为向量u，则下一时刻的市场占有率就是uP，再下一时刻的市场占有率就是uP^2，…，而且，市场占有率会逐步稳定到某个概率向量Z，即出现ZP=Z。这种稳定的市场占有率体现转移矩阵的特征，与初始时刻的市场占有率无关。

假设占领某地区市场的冰箱品牌A与B，每月市场占有率的变化可用如下常数转移矩阵来描述，则冰箱品牌A与B在该地区最终将逐步稳定到市场占有率（）。
$P=\begin{bmatrix} 0.8&0.2\\ 0.4&0.6\\ \end{bmatrix}$

解析：
常数矩阵为
$P=\begin{bmatrix} 4/5&1/5\\ 2/5&3/5\\ \end{bmatrix}$
分别把每个选项的1行2列矩阵与此常数矩阵做矩阵乘法，得到的结果仍然是选项，则此选项就是正确答案： $\begin{bmatrix}2/3&1/3\\\end{bmatrix}$

时间

工程、进度、工期计算，一般可采用甘特图。

最小工期

某企业拟生产甲、乙、丙、丁四个产品。每个产品必须依次由设计部门、制造部门和检验部门进行设计、制造和检验，每个部门生产产品的顺序是相同的。各产品各工序所需的时间如下表所示（单位：天）。只要适当安排好产品生产顺序，该企业最快可以在（）天全部完成这四个产品。

产品	设计	制造	检验
甲	13	15	20
乙	10	20	18
丙	20	16	10
丁	8	10	15

解析：节省时间的安排方法必然是紧随衔接和尽可能并行安排生产。第1个产品的设计和最后1个产品的检验是无法与其他工作并行进行的，因此，应安排首个设计时间+末个检验时间尽可能短。因此，先安排生产丁，最后安排生产丙。有两种实施方案：

丁、甲、乙、丙顺序，则共需8+13+15+20+18+10=84天，如下图所示：
丁、乙、甲、丙顺序，则共需8+10+20+18+20+10=86天，如下图所示：

丁、甲、乙、丙顺序
在这里插入图片描述
丁、乙、甲、丙顺序

期望时间

某项目包括A~G七个作业，各作业之间的衔接关系和所需时间如下表。其中，作业C所需的时间，乐观估计为5天，最可能为14天，保守估计为17天。假设其他作业都按计划进度实施，为使该项目按进度计划如期全部完成，作业C（）。
A. 必须在14天内完成
B. 必须在期望时间内完成
C. 比期望时间最多可拖延1天
D. 比期望时间最多可拖延2天

作业	A	B	C	D	E	F	G
紧前作业	-	A	A	B	C,D	-	E,F
所需天数	5	7		8	3	20	4

解析：
做此题时，必须要套用公式（知道什么公式，并且要记住），否则就是在瞎蒙：期望时间=(乐观时间+4*最可能时间+保守时间)/6。套用公式，期望时间为13天。

然后绘制一下路径图：
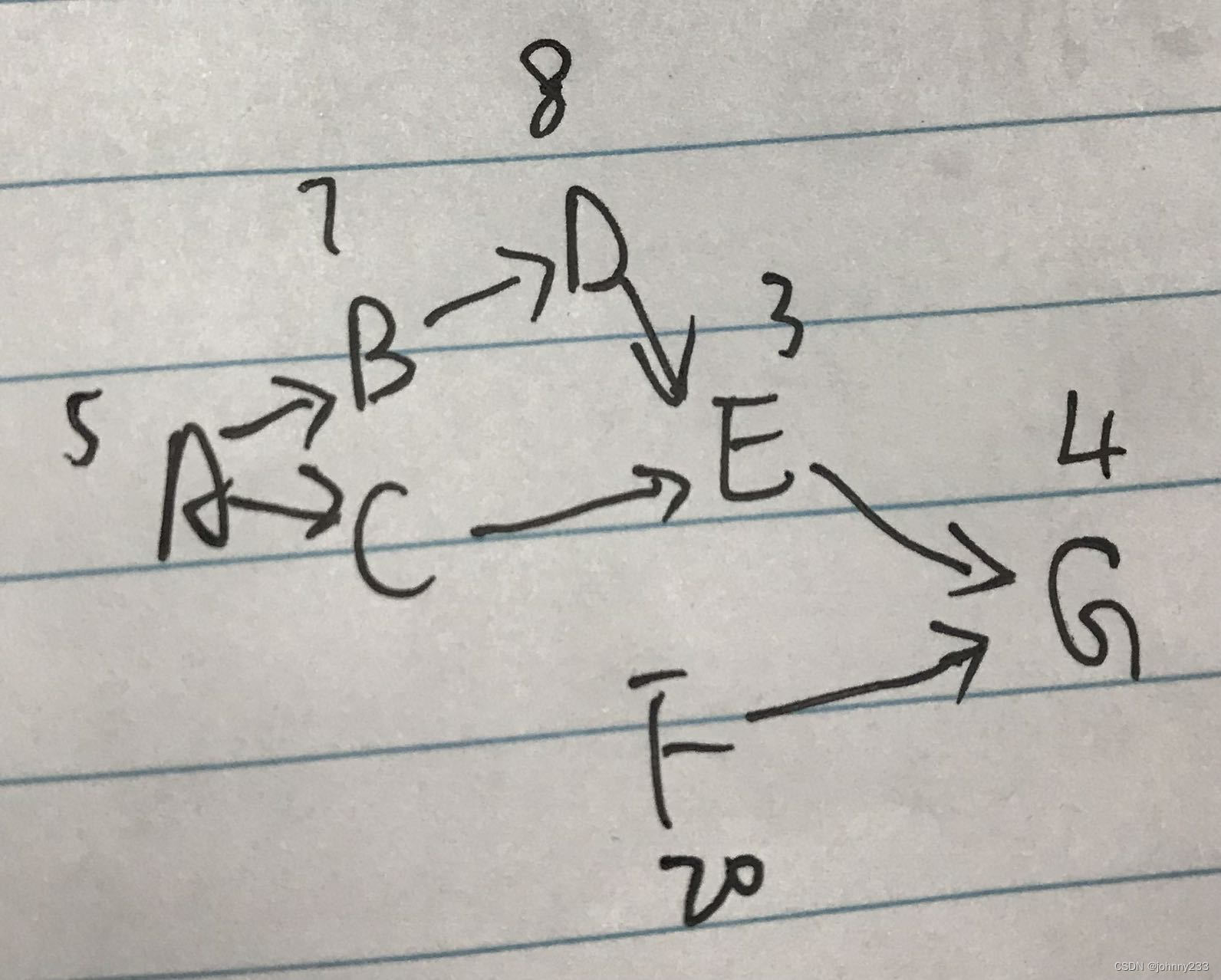
在这里插入图片描述
可以只考虑A到E的两条路径：

ABDE，天数为23天
ACE，天数为8+13=21天

所以，答案应该是D. 比期望时间最多可拖延2天

路径

最大流量

在军事演习中，张司令希望将部队尽快从A地通过公路网运送到F地，图中标出各路段上的最大运量（单位：千人/小时），从A地到F地的最大运量是（）千人/小时。
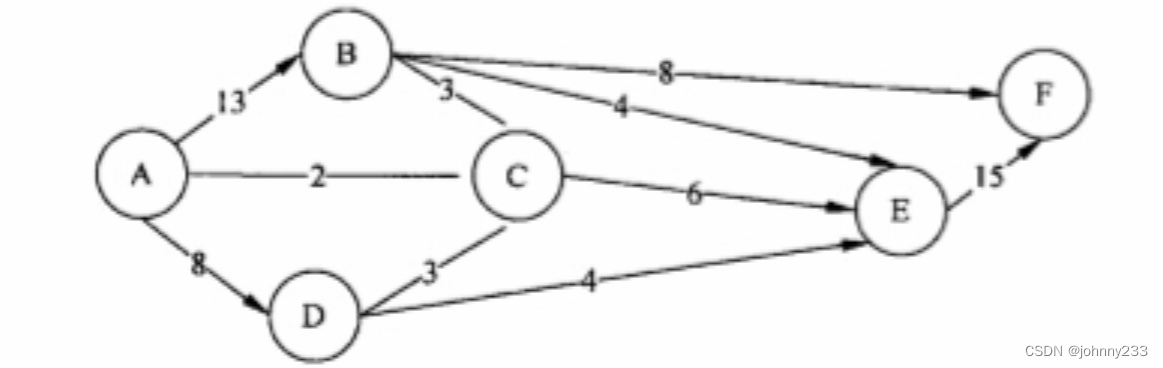
在这里插入图片描述
解析：
怎么理解运量？

从A到F有多条路径，总的最大运量应等于每条路径上的最大运量之和。每条路径上有多段，每条路径上的最大运量应是各路段最大运量的最小值。多条路径可以共享同一路段，该路段上的流量等于所有各条路径上的流量之和。

计算步骤如下（步骤并不唯一，但计算结果最大流量值应该是一致的）：

ABF最大流量8（AB剩余流量5，BF断开）
ABEF最大流量4（AB剩余流量1，BE断开，EF剩余流量11）
ABCEF最大流量1（AB断开，BC剩余流量2，CE剩余流量5，EF剩余流量10）
ACEF最大流量2（AC断开，CE剩余流量3，EF剩余流量8）
ADCEF最大流量3（AD剩余流量5，DC和CE断开，EF剩余流量5）
ADEF最大流量4（AD剩余流量1，DE断开，EF剩余流量1）
AF总的最大流量等于8+4+1+2+3+4=22（千人/小时）。

关键路径

下图为某项目规划的的进度网络图（单位：周）。在实际实施过程中，活动B-E比计划延迟2周，活动J-K比计划提前3周，则该项目的关键路径是（），总工期是（）周。
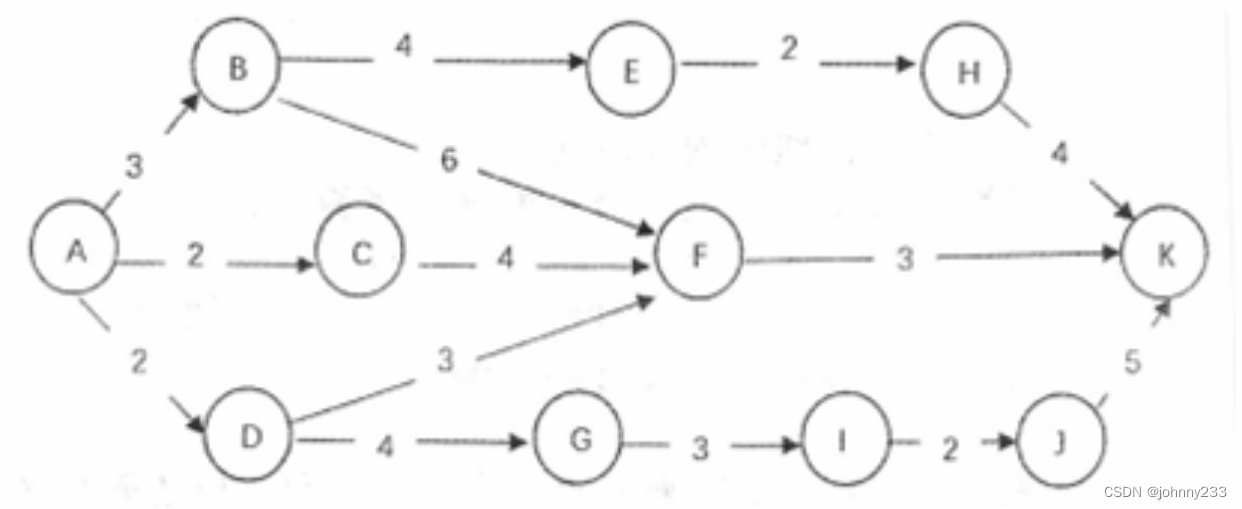
在这里插入图片描述
解析：
关键路径就是耗时最长的路径：ABEHK；
总工期为：3+6+2+4=15周。

总利润

物资、资源分配，利润最大化。一般可以用方程、排列组合、决策树等多种方法求解。

利润

某公司需要将4吨贵金属材料分配给下属的甲、乙、丙三个子公司（单位：吨）。据测算，各子公司得到这些材料后所能获得的利润（单位：万元）见下表。根据此表，只要材料分配适当，该公司最多可以获得利润（）万元。

子公司\材料	1吨	2吨	3吨	4吨
甲	4	7	10	13
乙	5	9	11	13
丙	4	6	11	14

解析：
最笨的方法，排列组合，分别给甲乙丙2吨，另外两家子公司各1吨。当然也有全部分给某个子公司，以及给某个子公司分3吨的情况。

最佳分配方法：甲1吨+乙2吨+丙1吨，利润为4+4+9=17。

产出

某服装店有甲、乙、丙、丁四个缝制小组。甲组每天能缝制5件上衣或6条裤子；乙组每天能缝制6件上衣或7条裤子；丙组每天能缝制7件上衣或8条裤子；丁组每天能缝制8件上衣或9条裤子。每组每天要么缝制上衣，要么缝制裤子，不能弄混。订单要求上衣和裤子必须配套（每套衣服包括一件上衣和一条裤子）。只要做好合理安排，该服装店15天最多能缝制（）套衣服。

解析：
甲、乙、丙、丁四组做上衣和裤子的效率之比分别为5/6、6/7、7/8、8/9，并且依次增加。因此，丁组做上衣效率更高，甲组做裤子效率更高。为此，安排甲组15天全做裤子，丁组15天全做上衣。设乙组用x天做上衣，15-x天做裤子；丙组用y天做上衣，15-y天做裤子，为使上衣和裤子配套，则有0+6x+7y+8*15=6*15+7(15-x)+8(15-y)+0，即：13x+15y=13*15，y=13-13x/15，15天共做套数6x+7y+8*15=6x+7(13-13x/15)+120=211-x/15，只有在x=0时，最多可做211套。此时，y=13，即甲乙丙丁四组分别用0、0、13、15天做上衣，用15、15、2、0天做裤子。

总收益

生产某种产品有两个建厂方案：

建大厂，需要初期投资500万元。如果产品销路好，每年可以获利200万元；如果销路不好，每年会亏损20万元
建小厂，需要初期投资200万元。如果产品销路好，每年可以获利100万元；如果销路不好，每年只能获利20万元

市扬调研表明，未来2年这种产品销路好的概率为70%。如果这2年销路好，则后续5年销路好的概率上升为80%；如果这2年销路不好，则后续5年销路好的概率仅为10%。为取得7年最大总收益，决策者应（）。

解析：
采用决策树分析方法解答如下：
先画决策树，从左至右逐步画出各个决策分支，并在各分支上标出概率值，再在最右端分别标出年获利值。然后从右至左，计算并填写各节点处的期望收益。
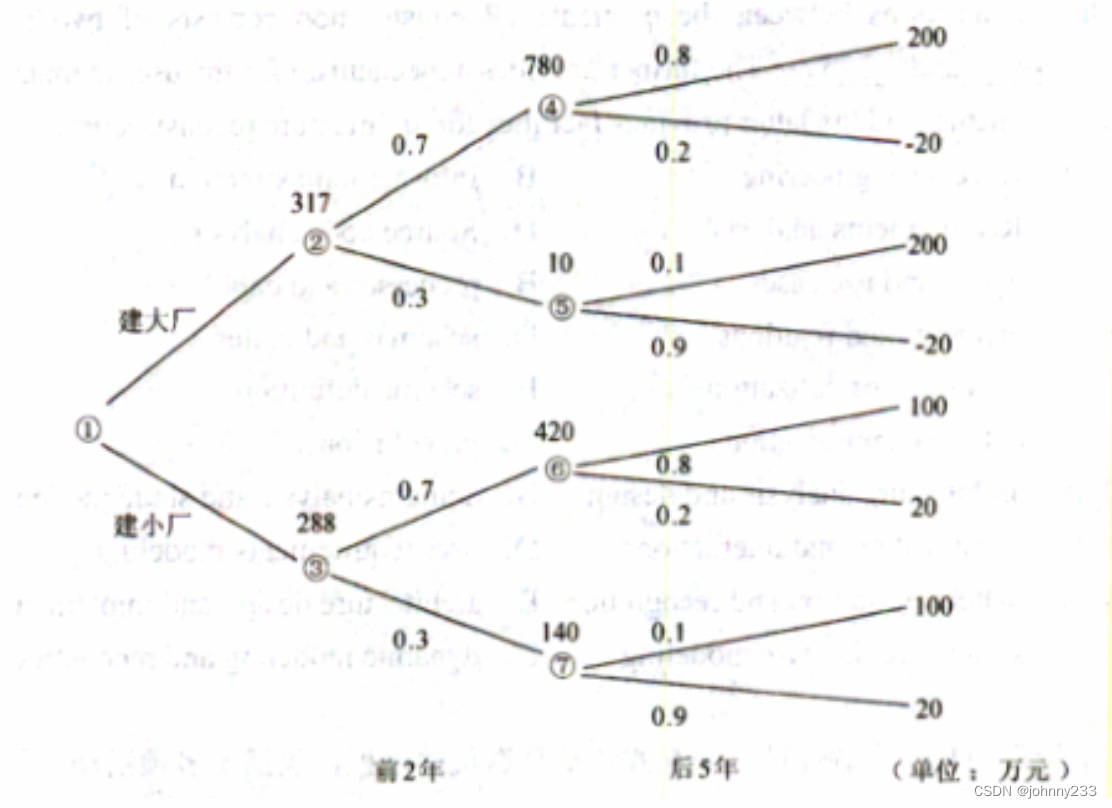
在这里插入图片描述
在右面四个节点处依次按下列算式计算5年的期望值，并将结果分别写在节点处：
节点④：(200*0.8-20*0.2)*5=780
节点⑤：(200*0.1-20*0.9)*5=10
节点⑥：(100*0.8+20*0.2)*5=420
接点⑦：(100*0.1+20*0.9)*5=140