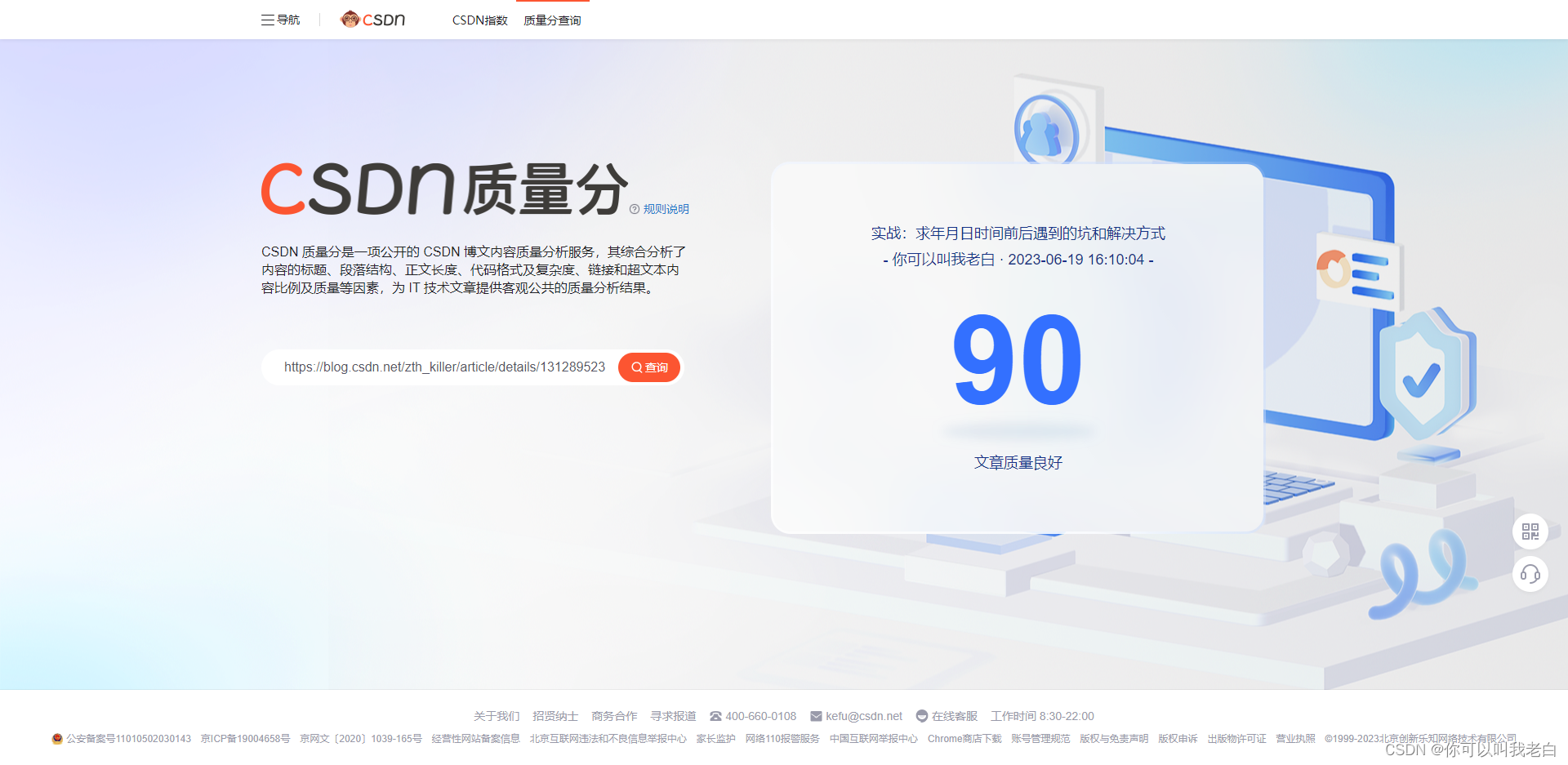
问题的关键在于：人们是否考虑过大背景/先验/问题的前提，从而做出一个大致的估计。这就引出了我们关于理性的探讨，理性不是说知道事实，而是认识到哪些因素是有关的。

x.1 一个关于贝叶斯定理的例子

引入一个steve假设。我们已知大背景下图书管理员比上农民的比例是1:20，在得到一个新证据后（一段关于steve的描述），认为有40%的图书管理员符合新给定的证据，而只有10%的农民符合新给定的证据。但是考虑到大背景下，最终我们得到steve是图书馆管理员的概率是很低的。

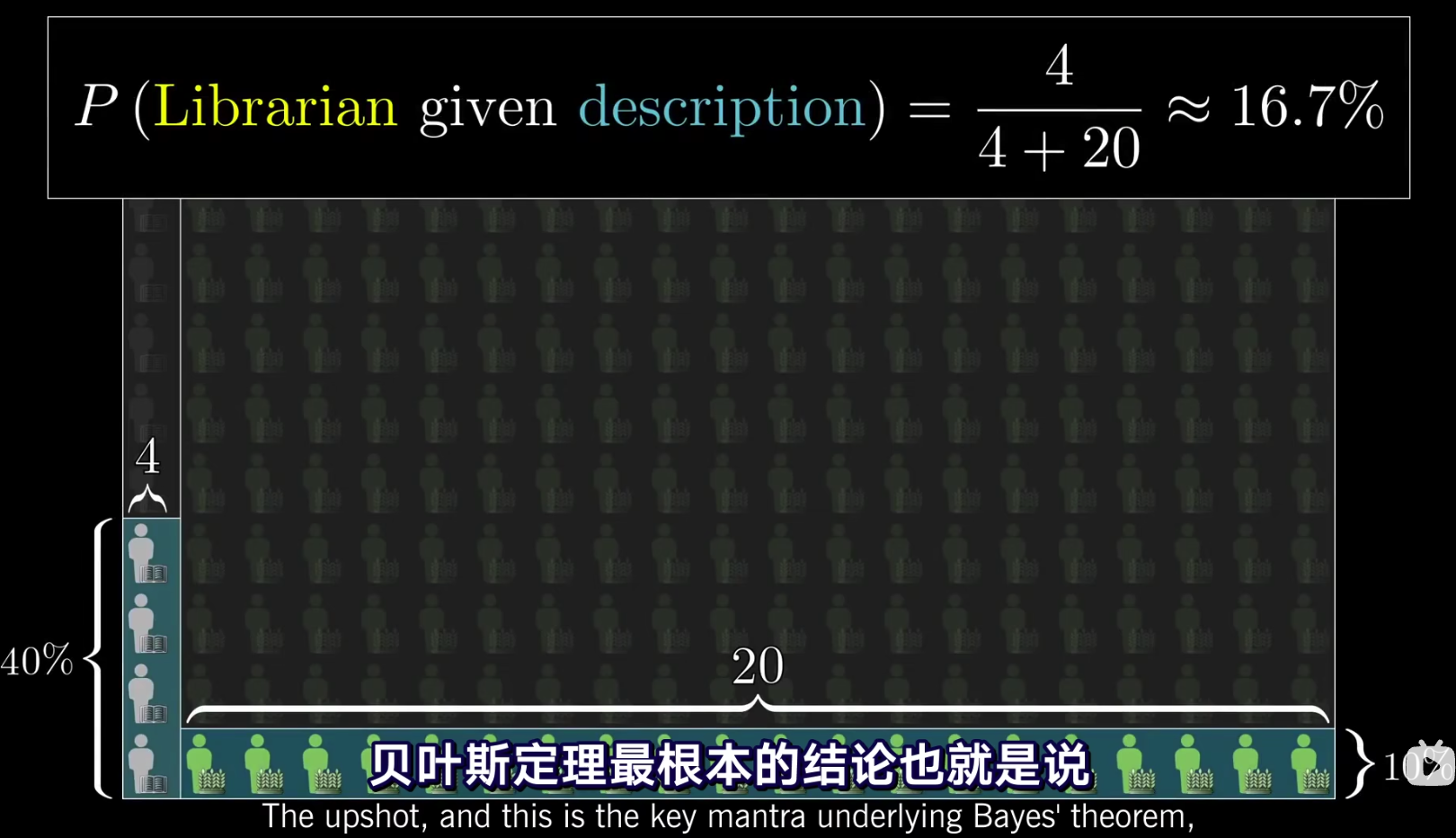
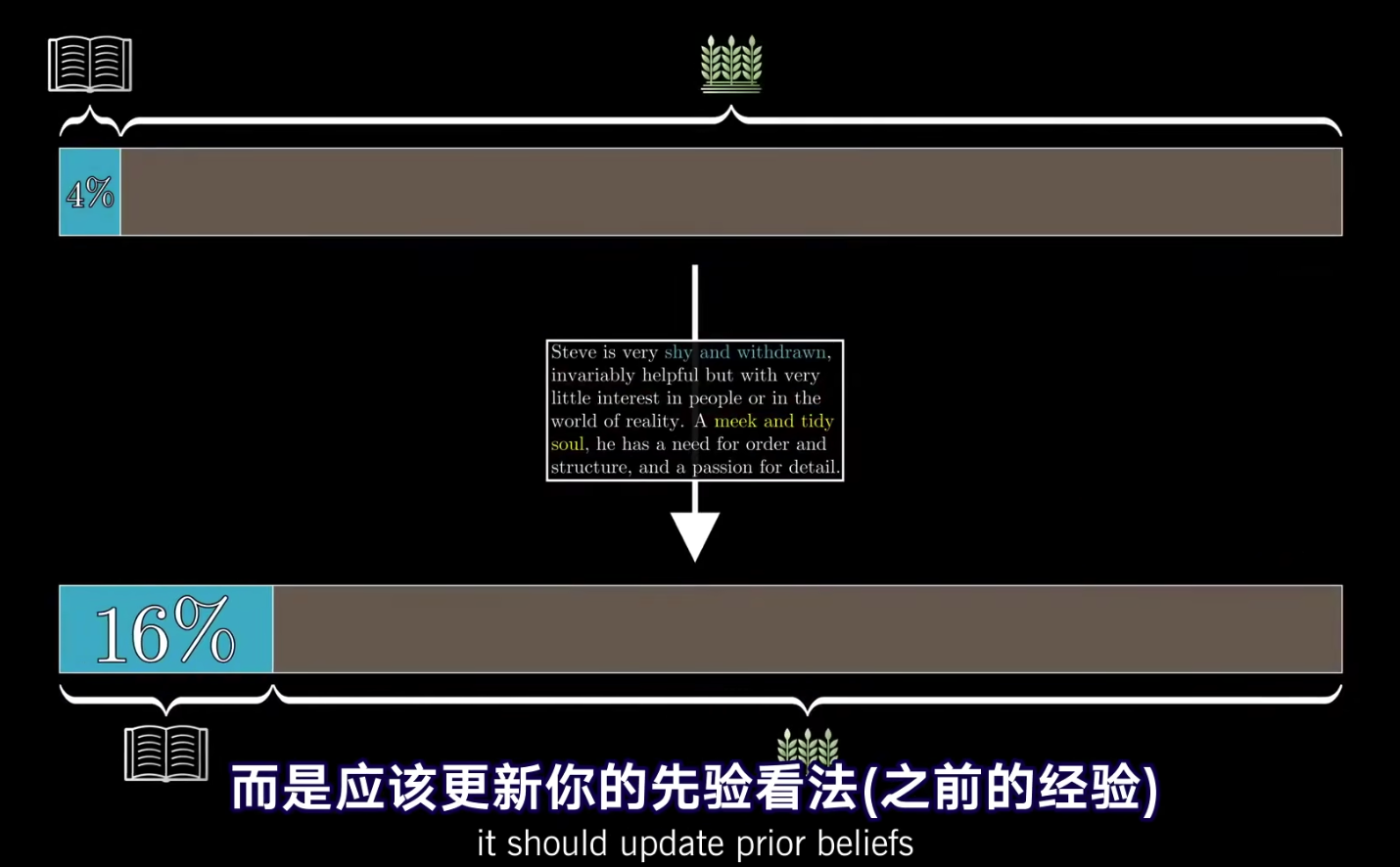
贝叶斯的核心要义在于：新证据不能凭空决定看法，而只是更新先验看法（这里的先验指的是之前的经验，即已知的大背景）。如下，便是将4%的图书管理员更新为了16%。

x.2 贝叶斯定理是什么

贝叶斯定理即是考虑到所有的证据后，再计算概率的方法。

公式如下：

x.3 何时使用贝叶斯

关于什么时候使用贝叶斯：当你已知多个证据（背景和引入新证据）时，且你要求解在引入新证据后你假设仍然成立的概率，此时就可以使用贝叶斯。

首先你有一个假设/命题（例如steve是个图书管理员），其次你知道一些新的证据（关于steve的描述=>40%的图书管理员符合描述，而只有10%的农民符合描述），现在你想结合新得到的证据，再结合大背景/证据/统计量/先验前提下（图书馆管理员：农民=1:20），求得你假设成立的概率P(H|E)：

x.4 如何使用贝叶斯/贝叶斯的使用流程

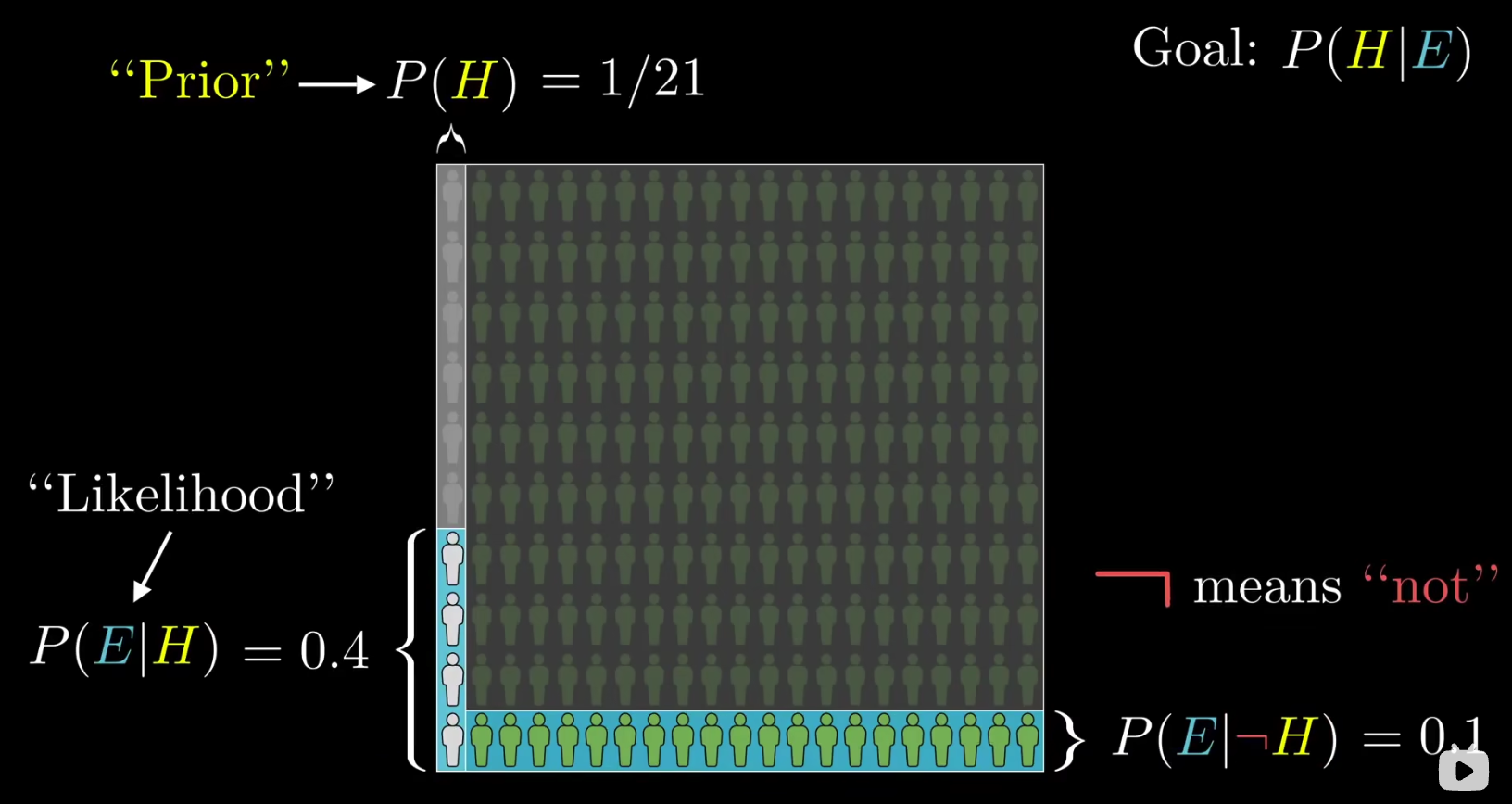
1. 首先你有一个假设H: steve是图书管理员，其次我们知道在大背景中，这个假设成立的prior先验概率为P(H)=1/21

他来自于大背景下图书管理员和农民的比例。

2. 第二步，在得到一个新证据后，我们的先验概率空间就被压缩了，这一步的关键在于，新证据的引入对左边和右边的限制程度是不一样的。在这一步中，我们需要知道在假设成立条件下，我们看到的证据的概率（likelihood似然）

这个步骤其实是为了方便求解在人群中，符合新证据的图书管理员个数$=sum\ast P(H)\ast P(E|H)$

3. 第三步，你需要知道在假设不成立条件下，你看到的证据的likelihood似然

即在人群中，符合新证据的农民个数$=sum\ast P(\neg H)\ast P(E|\neg H)$

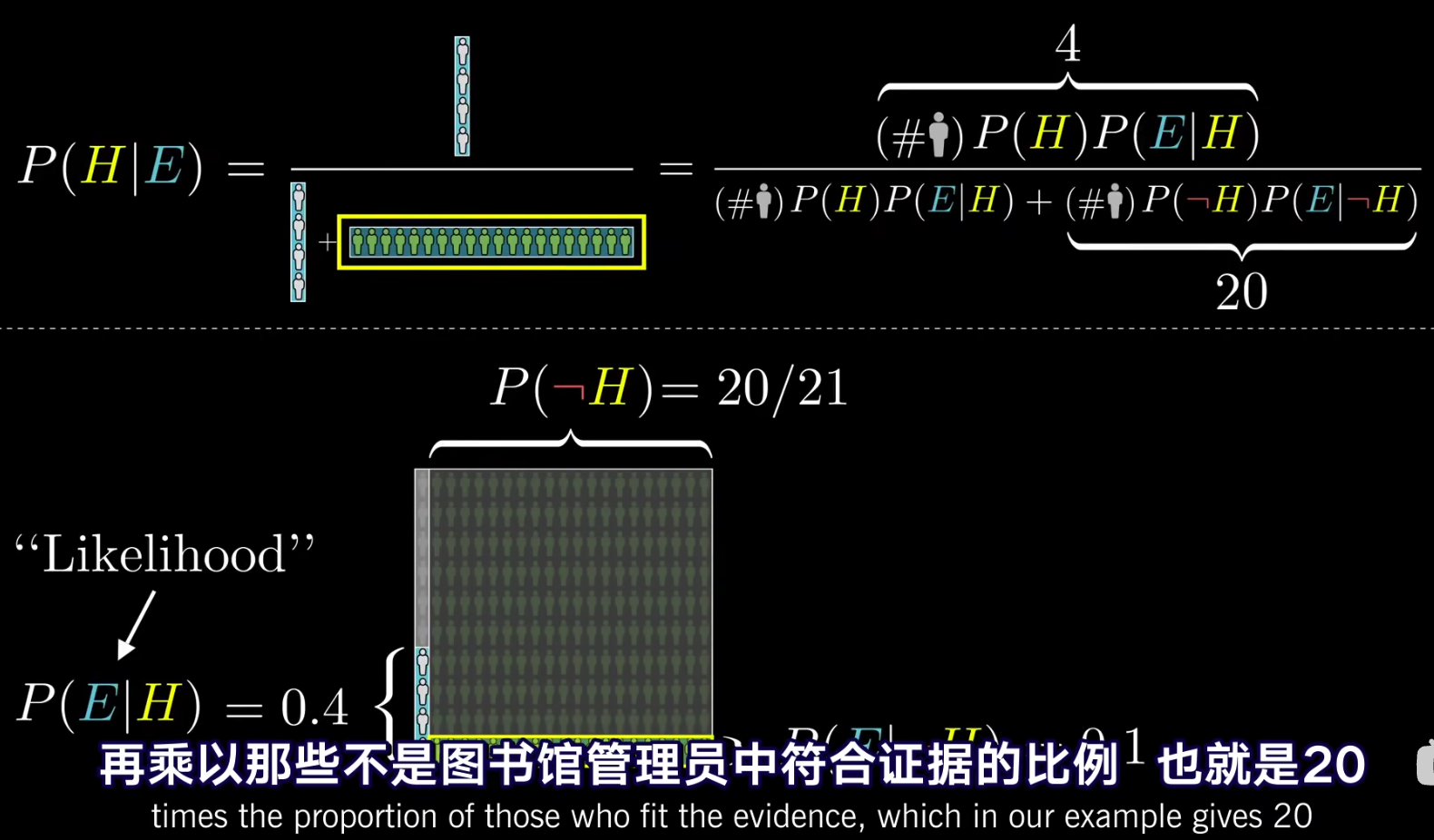
4. 最终我们计算总数并使用古典概型计算posterior后验概率

5. 化简公式，得到只有概率的抽象表达形式。注：分式的分母部分是全概率公式P(E) - 即看到证据的概率和，可以用互斥+全集分解的思想展开成任意形式。

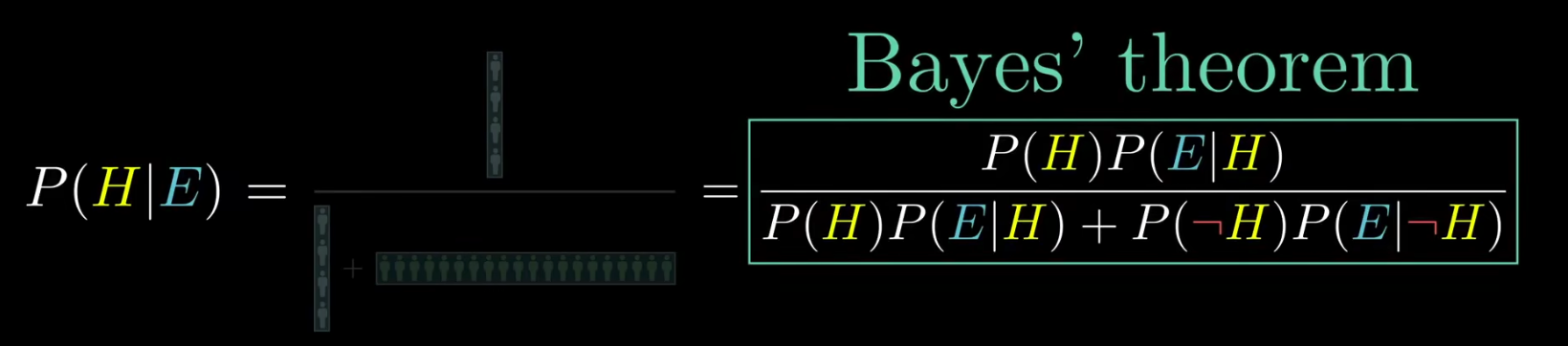
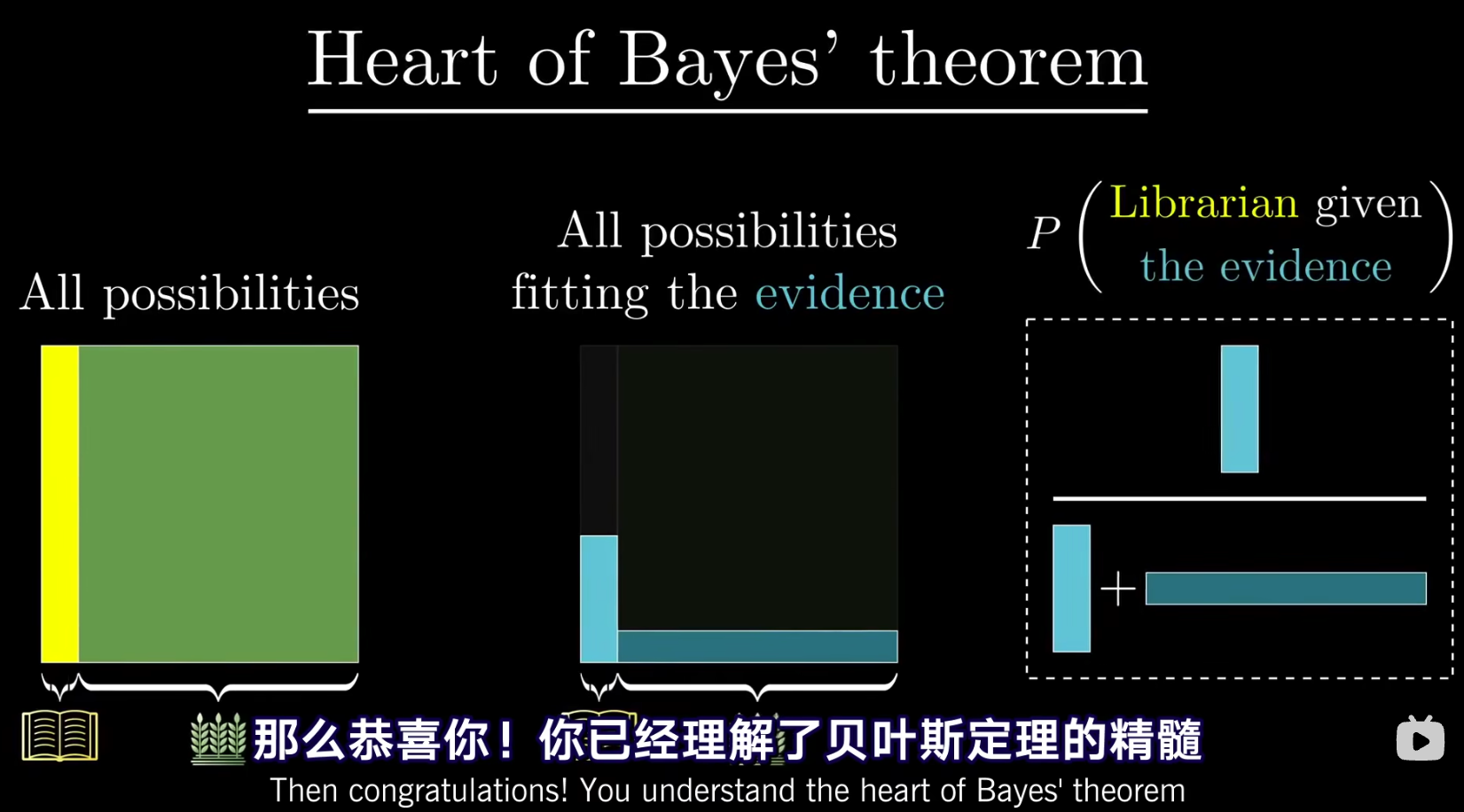
x.6 快速记忆贝叶斯公式

我们选择通过图像记忆贝叶斯。

大背景下，先验概率将事件发生概率划分为两部分

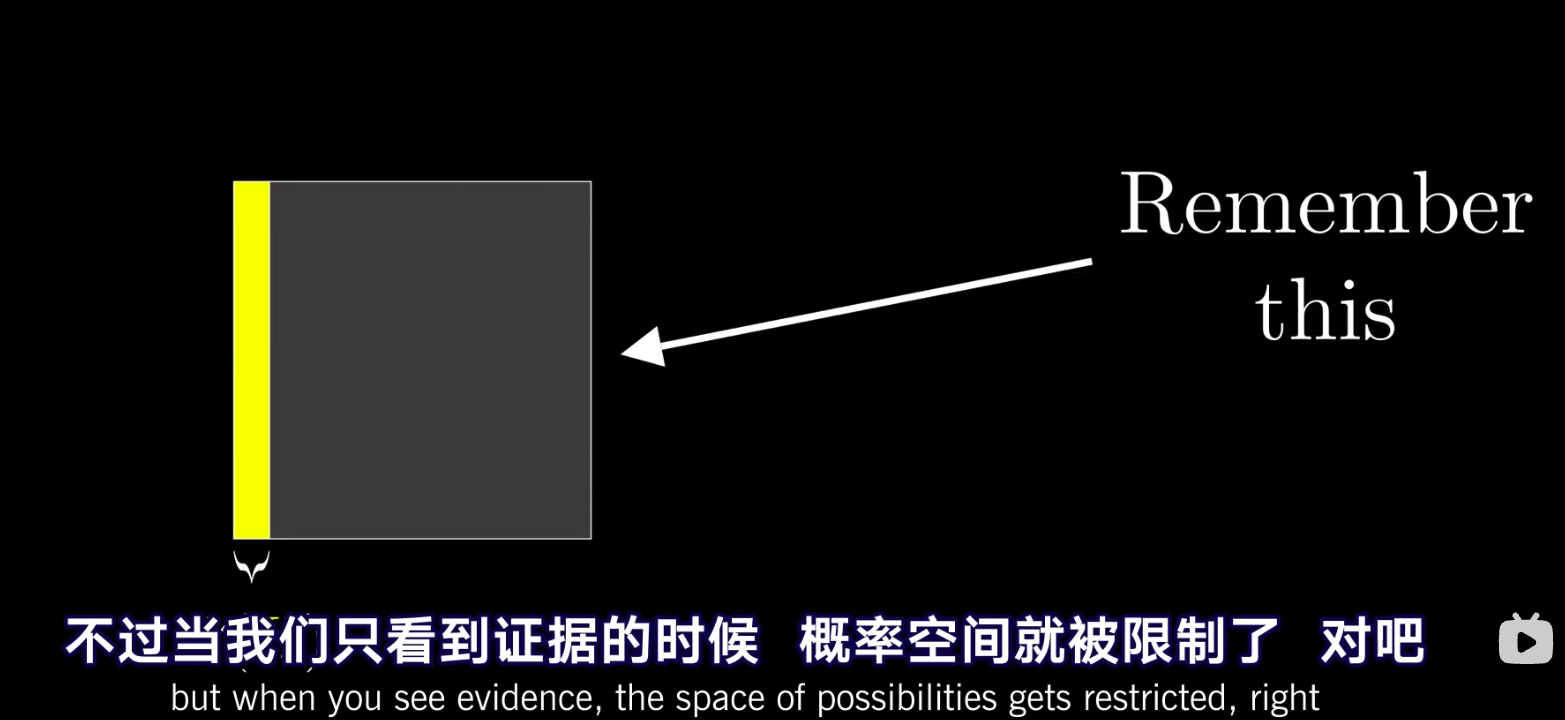
引入新证据后，压缩事件发生概率

得到贝叶斯公式