多状态Dp问题——买卖股票的最佳时机含冷冻期-编程知识

多状态Dp问题——买卖股票的最佳时机含冷冻期

一，题目

二，题目接口

三，解题思路及其代码

一，题目

给定一个整数数组prices，其中第 prices[i] 表示第 i 天的股票价格。

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:
输入: prices = [1,2,3,0,2]
输出: 3 
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
示例 2:
输入: prices = [1]
输出: 0

二，题目接口

class Solution {
public:int maxProfit(vector<int>& prices) {}
};

三，解题思路及其代码

首先，要明确的一点便是这道题还是一个多状态的dp问题。在这样一道题里面，在每一天都会有三种状态：1.今天处于卖出状态。

2.今天处于买入状态。

3.今天处于冷冻期。

在明确好这些状态以后，便可以开始列举这几种状态间的转换关系了。

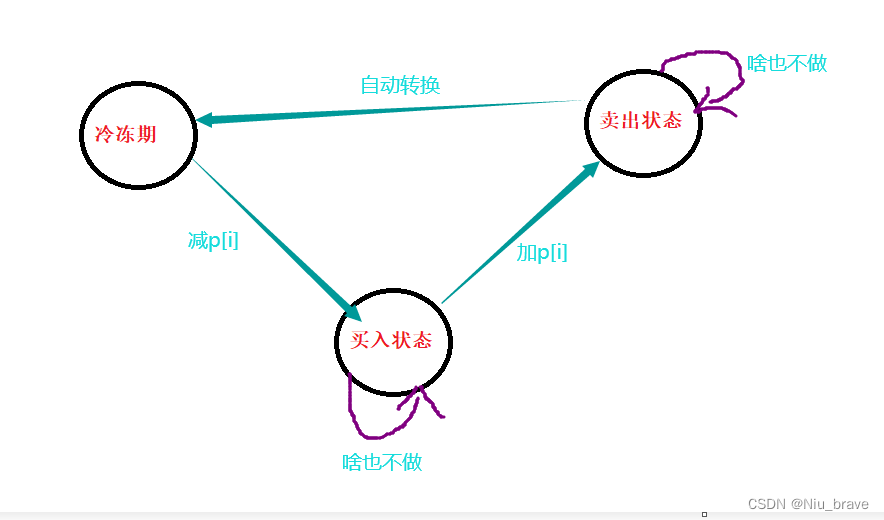
转换到卖出状态的情况：1.前一天处于买入状态，今天卖出股票。3.前一天处于卖出状态，这一天什么也不做。

转换到买入状态：1.前一天处于冷冻期状态，今天买入。2.前一天处于买入状态，今天啥也不做。

转换到冷冻期：1.前一天处于卖出状态。

画出状态转移图如下：

在推理完这些状态转移关系以后便可以推导出要求最大值的情况下的状态转移方程，设：f(i),g(i),x(i)分别是卖出状态，买入状态，冷冻期的最大利润。那便可以推导出如下的状态转移方程：
 f[i] = max(x[i-1]-prices[i],f[i-1]);g[i] = max(f[i-1]+prices[i],g[i-1]);x[i] = g[i-1];
然后在完成初始化以后便可以写出这道题的动态规划解法了，代码如下：
class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();vector<int>f(n);auto g = f;auto x = f;f[0]= -prices[0];//初始化for(int i = 1;i<n;i++){f[i] = max(x[i-1]-prices[i],f[i-1]);g[i] = max(f[i-1]+prices[i],g[i-1]);x[i] = g[i-1];}return max(x[n-1],g[n-1]);}
};