从《lc42 接雨水》到《lc84 柱状图中的最大矩形》-编程知识

1 LC42 接雨水

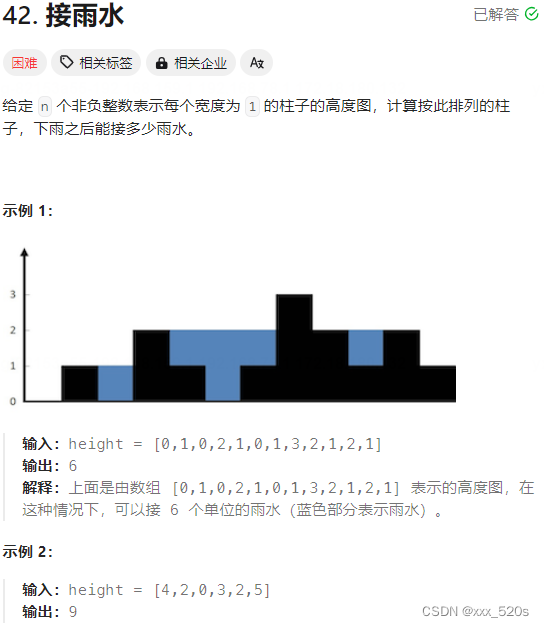
在这里插入图片描述

1.1 答案

解法四：双指针
动态规划中，我们常常可以对空间复杂度进行进一步的优化。

例如这道题中，可以看到，max_left [ i ] 和 max_right [ i ] 数组中的元素我们其实只用一次，然后就再也不会用到了。所以我们可以不用数组，只用一个元素就行了。我们先改造下 max_left。

public int trap(int[] height) {int sum = 0;int max_left = 0;int[] max_right = new int[height.length];for (int i = height.length - 2; i >= 0; i--) {max_right[i] = Math.max(max_right[i + 1], height[i + 1]);}for (int i = 1; i < height.length - 1; i++) {max_left = Math.max(max_left, height[i - 1]);int min = Math.min(max_left, max_right[i]);if (min > height[i]) {sum = sum + (min - height[i]);}}return sum;
}作者：windliang
链接：https://leetcode.cn/problems/trapping-rain-water/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

我们成功将 max_left 数组去掉了。但是会发现我们不能同时把 max_right 的数组去掉，因为最后的 for 循环是从左到右遍历的，而 max_right 的更新是从右向左的。

所以这里要用到两个指针，left 和 right，从两个方向去遍历。

那么什么时候从左到右，什么时候从右到左呢？根据下边的代码的更新规则，我们可以知道

max_left = Math.max(max_left, height[i - 1]);

height [ left - 1] 是可能成为 max_left 的变量，同理，height [ right + 1 ] 是可能成为 right_max 的变量。

只要保证 height [ left - 1 ] < height [ right + 1 ] ，那么 max_left 就一定小于 max_right。

因为 max_left 是由 height [ left - 1] 更新过来的，而 height [ left - 1 ] 是小于 height [ right + 1] 的，而 height [ right + 1 ] 会更新 max_right，所以间接的得出 max_left 一定小于 max_right。

反之，我们就从右到左更。

  public int trap(int[] height) {int n=height.length;int ans=0;int lm=-1,rm=-1;int l=1,r=n-2;while(l<=r){if(height[l-1]<height[r+1]){ // #Alm=Math.max(lm,height[l-1]);if(lm>height[l]){ans+=lm-height[l];}l++;}else{rm=Math.max(rm,height[r+1]);if(rm>height[r]){ans+=rm-height[r];}r--;}}return ans;}

1.2 解析 #A 处的代码`if(height[l-1]<height[r+1])`, max_left不是还没有基于height[left - 1]更新吗，为什么能做出（由于max_left是基于高度[left - 1]更新的，并且高度[left - 1]小于高度[right + 1]，这更新了max_right，因此逻辑上可以得出max_left将小于或等于max_right。）的推断？这里是不是默认初始以及之后的max_left <=max_right,所以只需要比较height[left - 1]和heightright- 1

您的理解是正确的。在这个算法中，确实有一个隐含的假设，即在执行到当前步骤之前，max_left 通常小于或等于 max_right。这个假设是基于算法如何运行和如何更新这两个值的。

当算法比较 height[left - 1] 和 height[right + 1] 时，它实际上是在确定下一步应该如何移动指针，以便有效地计算积水量。这里的关键逻辑是：

如果 height[left - 1] < height[right + 1]:
- 这意味着左侧的边界较低。因此，我们可以假设 max_left（已经是左边的最高点）小于或等于 max_right。
- 在这种情况下，移动左指针是安全的，因为即使左边的墙较低，右边也有足够高的墙（max_right）来保持水。
如果 height[left - 1] >= height[right + 1]:
- 这表明右侧的边界较低，或者至少与左边相等。
- 因此，移动右指针是更安全的选择，因为左边有足够高的墙（max_left）来保持水。
更新 max_left 和 max_right:
- 在每一步中，max_left 和 max_right 都会根据当前指针位置的情况进行更新。

总的来说，这个算法的核心在于它尝试从较低的一侧开始计算积水量，这样可以保证在那一侧的计算过程中，另一侧总是有足够高的边界来支撑水位。这种方法使得算法既高效又准确。

2 LC84. 柱状图中最大的矩形

在这里插入图片描述

2.1 解题

推荐题解：lc84 柱状图中的最大矩形

class Solution {// 时间复杂度进一步常数级优化public int largestRectangleArea(int[] heights) {int n=heights.length;int ans=0;int[]l=new int[n];int[]r=new int[n];Arrays.fill(r,n);Deque<Integer>st=new LinkedList<>();int i=0;while(i<n){while(!st.isEmpty()&&heights[st.peekLast()]>=heights[i]){r[st.pollLast()]=i;}l[i]=st.isEmpty()?-1:st.peekLast();st.addLast(i);i++;}for(i=0;i<n;i++){ans=Math.max(ans, (r[i]-l[i]-1)*heights[i]);}return ans;}// 时间复杂度优化public int largestRectangleArea4(int[] heights) {int n=heights.length;int ans=0;int[]l=new int[n];int[]r=new int[n];Deque<Integer>st=new LinkedList<>();int i=0;while(i<n){while(!st.isEmpty()&&heights[st.peekLast()]>=heights[i]){st.pollLast();}l[i]=st.isEmpty()?-1:st.peekLast();st.addLast(i);i++;}st.clear();i=n-1;while(i>=0){while(!st.isEmpty()&&heights[st.peekLast()]>=heights[i]){st.pollLast();}r[i]=st.isEmpty()?n:st.peekLast();st.addLast(i);i--;}for(i=0;i<n;i++){ans=Math.max(ans, (r[i]-l[i]-1)*heights[i]);}return ans;}public int largestRectangleArea3(int[] heights) {int n=heights.length;int ans=0;// 按高度遍历，这里的遍历的是数组中所有出现的高度for(int i=0;i<n;i++){int j=i;while(j>=0&&heights[j]>=heights[i]){j--;}int k=i;while(k<n&&heights[k]>=heights[i]){k++;}ans=Math.max(ans,(k-j-1)*heights[i]);}return ans;}public int largestRectangleArea2(int[] heights) {int n=heights.length;int ans=0;for(int i=0;i<n;i++){int min=Integer.MAX_VALUE;for(int j=i;j<n;j++){min=Math.min(min, heights[j]);ans=Math.max(ans,(j-i+1)*min);}}return ans;}
}

3 相似之处

   // lc84 柱状图中的最大矩形 : 时间复杂度优化public int largestRectangleArea4(int[] heights) {int n=heights.length;int ans=0;int[]l=new int[n];int[]r=new int[n];Deque<Integer>st=new LinkedList<>();int i=0;while(i<n){while(!st.isEmpty()&&heights[st.peekLast()]>=heights[i]){st.pollLast();}l[i]=st.isEmpty()?-1:st.peekLast();st.addLast(i);i++;}st.clear();i=n-1;while(i>=0){while(!st.isEmpty()&&heights[st.peekLast()]>=heights[i]){st.pollLast();}r[i]=st.isEmpty()?n:st.peekLast();st.addLast(i);i--;}for(i=0;i<n;i++){ans=Math.max(ans, (r[i]-l[i]-1)*heights[i]);}return ans;}// lc42 接雨水public int trap(int[] height) {int n=height.length;int ans=0;int lm=-1,rm=-1;int l=1,r=n-2;while(l<=r){if(height[l-1]<height[r+1]){lm=Math.max(lm,height[l-1]);if(lm>height[l]){ans+=lm-height[l];}l++;}else{rm=Math.max(rm,height[r+1]);if(rm>height[r]){ans+=rm-height[r];}r--;}}return ans;}

3.1 这两个题解很相似

确实，从您提供的 LeetCode 问题 42 (“接雨水”) 和问题 84 (“柱状图中最大的矩形”) 的解题代码中，我们可以看到一些相似之处。尽管两个问题的实际目标不同，它们的解法都涉及到一些共同的编程技巧和思路。

相似点

单调栈的应用：
- 在问题 84 的解法中，使用单调栈（Deque<Integer> st）来维护一个单调递增的高度索引，这有助于确定每个条形的左右边界。
- 这种栈的应用在处理数组中的连续区间问题时非常有效，如寻找左右两侧第一个小于当前元素的位置。
双指针技术：
- 在问题 42 的解法中，使用左右双指针（l 和 r）来从两端向中间遍历数组。
- 这种技术允许在一次遍历中比较和处理两端的元素，是处理此类问题的常见方法。
局部最大/最小值的更新：
- 在问题 42 中，使用 lm 和 rm（左侧和右侧的最大高度）来更新局部最大值，并用这些值来计算积水量。
- 在问题 84 中，使用栈来计算每个条形的局部左右边界，再计算最大矩形面积。
动态计算过程中的条件判断：
- 在问题 42 中，通过比较 height[l-1] 和 height[r+1] 来决定是移动左指针还是右指针。
- 在问题 84 中，通过比较 heights[st.peekLast()] 和 heights[i] 来决定是继续在栈中添加新元素还是进行弹出操作。