【算法总结】归并排序专题(刷题有感)-编程知识

思考

一定要注意归并排序的含义，思考归并的意义。
主要分为两个步骤：

拆分
1. 每次对半分(mid = l +r >> 1)
2. 输入：raw整块，输出：raw左块+ raw右块
合并
1. 每次都要对raw左块、 raw右块按照某种规则进行合并
2. 输入：raw左块+ raw右块，输出：raw整块

知道两个步骤之后，可以总结其他的特点：

拆分阶段和合并阶段是一一对应的，只不过拆分阶段是raw的，合并阶段符合一定的性质(对于归并排序则满足有序性)。
拆分时，段内是无序的，合并时，每一段都是有序的(数值有序性)。合并是针对两个有序的段进行合并，所以会经常用到双指针算法。
如下图所示，在合并过程中，段内是数值有序，但是相对顺序被破坏了，而两个段之间的相对顺序是不变的。6、7、8相对于1、2、3的顺序是不变的，6、7、8依然在1、2、3的左边。

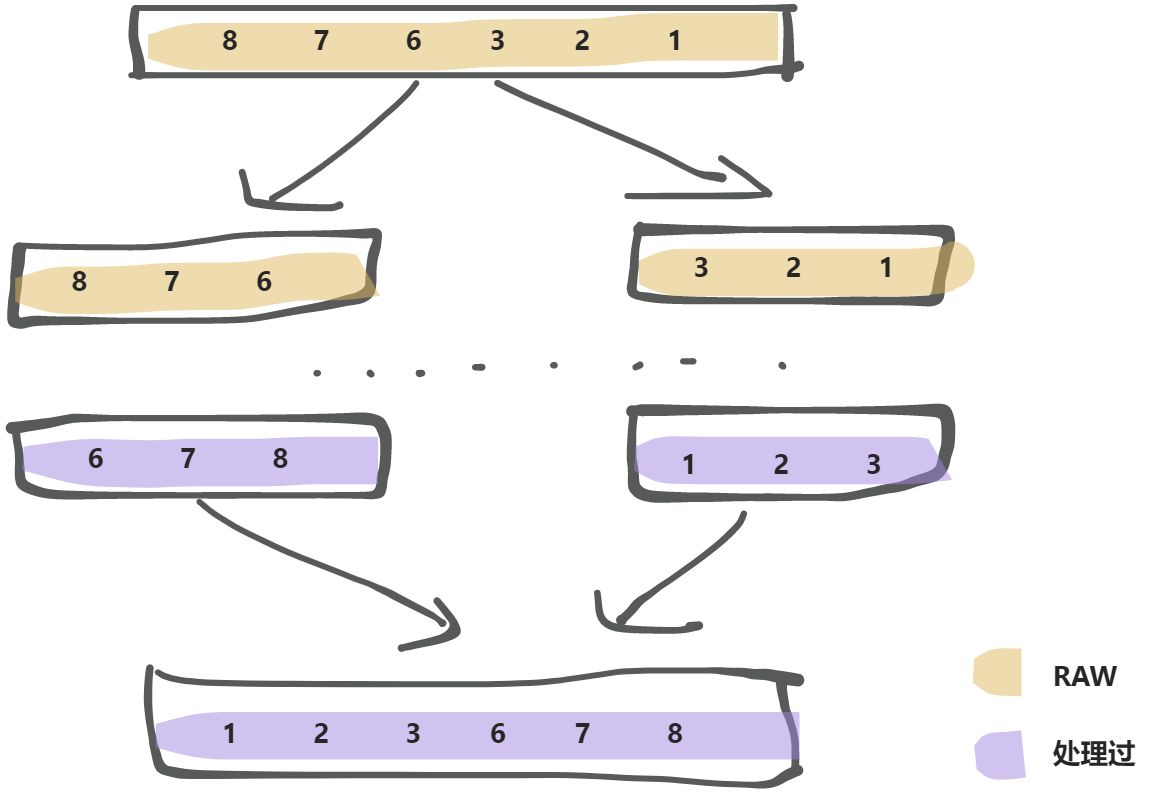
几道题做下来，感觉归并排序类型题的难点在于

题意的转化：重点就要题意是否支持将原模型分成两半来考虑，即计算左段相对后段的某种性质。
合并阶段对结果的计算，比如说求逆序对，那么合并的时候如何求逆序对的个数，双重循环遍历？双指针？等等。。。

普通模板

int* merge(int l, int r) {if (l > r) return nullptr;int* tmp = new int[r - l + 1];if (l == r) {tmp[0] = a[l];return tmp;}int mid = l + ((r - l) >> 1);int llen = mid - l + 1, rlen = r - mid;int* la = merge(l, mid);int* ra = merge(mid + 1, r);int i = 0, j = 0, cnt = 0;for (; i < llen && j < rlen; ) {if (la[i] > ra[j]) {tmp[cnt ++] = ra[j ++];} else {tmp[cnt ++] = la[i ++];}}// 上边的循环结束之后，可能存在一个数组还未完全遍历。while(i < llen) tmp[cnt ++] = la[i ++];while(j < rlen) tmp[cnt ++] = ra[j ++];return tmp;
}

Acwing 787. 归并排序

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>using namespace std;const int N = 100000 + 100;
int a[N], tmp[N];void merge(int q[], int l, int r) {if (l >= r) return;int mid = l + ((r - l) >> 1);merge(q, l, mid);merge(q, mid + 1, r);int i = l, j = mid + 1, cnt = 0;for (; i <= mid && j <= r; ) {if (q[i] > q[j]) {tmp[cnt ++] = q[j ++];} else {tmp[cnt ++] = q[i ++];}}while(i <= mid) tmp[cnt ++] = q[i ++];while(j <= r) tmp[cnt ++] = q[j ++];for (int i = l, j = 0; i <= r; i ++, j ++)q[i] = tmp[j];
}int main()
{int n;cin >> n;for (int i = 0; i < n; i ++) cin >> a[i];merge(a, 0, n - 1);for (int i = 0; i < n; i ++) {printf("%d ", a[i]);}printf("\n");
}

Acwing 788. 逆序对的数量

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;typedef long long LL;const int N = 100100;int a[N];
int n;
LL ans;void print_arr(int* arr, int size) {for (int i = 0; i < size; i ++) {printf("%d ", arr[i]);}printf("\n");
}int* merge(int l, int r) {if (l > r) return nullptr;int* tmp = new int[r - l + 1];if (r == l) {tmp[0] = a[l];return tmp;}int mid = l + r >> 1;int* larr = merge(l, mid);int* rarr = merge(mid + 1, r);int llen = (mid - l) + 1, rlen = (r - mid - 1) + 1;// printf("l:\n");// print_arr(larr, llen);// printf("r:\n");// print_arr(rarr, rlen);int i = 0, j = 0, cnt = 0;for (; i < llen && j < rlen;){if (larr[i] > rarr[j]) {ans += (llen - 1 - i) + 1;tmp[cnt ++] = rarr[j ++];} else {tmp[cnt ++] = larr[i ++];}}while(i < llen) tmp[cnt ++] = larr[i ++];while(j < rlen) tmp[cnt ++] = rarr[j ++];// printf("merge\n");// print_arr(tmp, (r - l) + 1);// printf("ans : %d\n", ans);return tmp;
}int main()
{cin >> n;for (int i = 0; i < n; i ++) cin >> a[i];int* h = merge(0, n - 1);// for (int i = 0; i < n; i ++) {//     printf("%d\n", h[i]);// }printf("%lld\n", ans);return 0;
}

Leetcode 493. 翻转对

class Solution {long ans = 0;public int reversePairs(int[] nums) {int n = nums.length;mergeSort(nums, 0, n - 1);return (int)ans;}void mergeSort(int[] nums, int l, int r) {if (l >= r) return;int[] tmp = new int[r - l + 1];int mid = l + ((r - l) >> 1);mergeSort(nums, l, mid);mergeSort(nums, mid + 1, r);int i = l, j = mid + 1, cnt = 0;int base = 0;for (; i <= mid; i ++) {while (j <= r && (long)nums[i] > 2L * nums[j]) {j ++;}ans += (j - (mid + 1));}i = l;j = mid + 1;for (; i <= mid && j <= r; ) {if (nums[i] > nums[j]) tmp[cnt ++] = nums[j ++];else tmp[cnt ++] = nums[i ++];}while(i <= mid) tmp[cnt ++] = nums[i ++];while(j <= r) tmp[cnt ++] = nums[j ++];for (int k = 0; k < cnt; k ++)nums[l + k] = tmp[k];}
}

Leetcode 315. 计算右侧小于当前元素的个数

这个题比较恶心的就是要维护元素原来的位置

class Node {int x;int id;Node(int x, int id) {this.x = x;this.id = id;}
}class Solution {List<Integer> ans = null;public List<Integer> countSmaller(int[] nums) {int n = nums.length;ans = new ArrayList<>(Collections.nCopies(n, 0));Node[] nodes = new Node[n];for (int i = 0; i < n; i ++) {nodes[i] = new Node(nums[i], i);}merge(nodes, 0, n - 1);return ans;}void merge(Node[] nodes, int l, int r) {if (l >= r) return;Node[] tmp = new Node[r - l + 1];int mid = l + ((r - l) >> 1);merge(nodes, l, mid);merge(nodes, mid + 1, r);int i = l, j = mid + 1, cnt = 0;int base = 0;for (; i <= mid;) {if (j == r + 1 || nodes[i].x <= nodes[j].x) {ans.set(nodes[i].id, ans.get(nodes[i].id) + base);tmp[cnt ++] = nodes[i ++];} else {tmp[cnt ++] = nodes[j ++];base ++;}}while (j <= r) tmp[cnt ++] = nodes[j ++];for (int k = 0; k < cnt; k ++)nodes[l + k] = tmp[k];}
}

Leetcode 327. 区间和的个数(前缀和)

这个题首先要想到利用前缀和将原来的数组进行转换。
要求的是区间和属于[lower, upper]区间的个数，转化为数学符号之后就是这样： $l o w er <= s u m [i] - s u m [j] <= u pp er$
1. 对于这样的不等式，可以分两步来考虑：
  1. 将连续不等式拆分成单个不等式， $s u m [i] - s u m [j] <= u pp er$
  2. 将变量i固定，求另外一个变量的值
2. 之后对于刚才的连续不等式就可以计算出符合条件的区间[m, n]
计算符合条件的区间的时机：在合并阶段，i的范围是[mid + 1, r]

class Solution {int lower = 0, upper = 0, ans = 0;public int countRangeSum(int[] nums, int lower, int upper) {this.upper = upper;this.lower = lower;int n = nums.length;long[] pre = new long[n + 1];for (int i = 1; i <= n; i ++)pre[i] = pre[i - 1] + nums[i - 1];merge(pre, 0, n);return ans;}void merge(long[] nums, int l, int r) {if (l >= r) return;long[] tmp = new long[r - l + 1];int mid = l + ((r - l) >> 1);merge(nums, l, mid);merge(nums, mid + 1, r);// 核心代码for (int i = mid + 1, j = l, k = l; i <= r; i ++) {while (j <= mid && nums[i] - nums[j] > upper) j ++;while (k <= mid && nums[i] - nums[k] >= lower) k ++;ans += k - j;}int cnt = 0;for (int i = l, j = mid + 1; i <= mid || j <= r; ) {if (i == mid + 1) tmp[cnt ++] = nums[j ++];else if (j == r + 1) tmp[cnt ++] = nums[i ++];else {if (nums[i] > nums[j])tmp[cnt ++] = nums[j ++];elsetmp[cnt ++] = nums[i ++];}}for (int i = 0; i < cnt; i ++)nums[i + l] = tmp[i];}
}

Acwing 65. 数组中的逆序对

题意就在题面上，所以直接套模板。

class Solution {int ans = 0;public int inversePairs(int[] nums) {int n = nums.length;mergeSort(nums, 0, n - 1);return ans;}void mergeSort(int[] nums, int l, int r) {if (l >= r) return;int[] tmp = new int[r - l + 1];int mid = l + ((r - l) >> 1);mergeSort(nums, l, mid);mergeSort(nums, mid + 1, r);int i = l, j = mid + 1, cnt = 0;for (; i <= mid && j <= r; ) {if (nums[i] > nums[j]) {ans += (mid - i) + 1;tmp[cnt ++] = nums[j ++];} else {tmp[cnt ++] = nums[i ++];}}while (i <= mid) tmp[cnt ++] = nums[i ++];while (j <= r) tmp[cnt ++] = nums[j ++];for (int k = 0; k < cnt; k ++)nums[l + k] = tmp[k];}}

Acwing 107. 超快速排序

根据题意可以分析出本题是要求逆序的数量， 那就直接套模板。

import java.util.Scanner;class Main {static long ans = 0;public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = 0;while((n = sc.nextInt()) != 0) {ans = 0;int[] nums = new int[n];    for (int i = 0; i < n; i ++) {nums[i] = sc.nextInt();}mergeSort(nums, 0, n - 1);System.out.println(ans);}}static void mergeSort(int[] nums, int l, int r) {if (l >= r) return;int[] tmp = new int[r - l + 1];int mid = l + ((r - l) >> 1);mergeSort(nums, l, mid);mergeSort(nums, mid + 1, r);int i = l, j = mid + 1, cnt = 0;for (; i <= mid && j <= r; ) {if (nums[i] > nums[j]) {ans += (mid - i) + 1;tmp[cnt ++] = nums[j ++];} else {tmp[cnt ++] = nums[i ++];}}while (i <= mid) tmp[cnt ++] = nums[i ++];while (j <= r) tmp[cnt ++] = nums[j ++];for (int k = 0; k < cnt; k ++)nums[l + k] = tmp[k];}}