AC修炼计划（AtCoder Regular Contest 162）-编程知识

传送门：AtCoder Regular Contest 162 - AtCoder

A题签到

B - Insertion Sort 2

我们可以从头开始一个一个排序，把1通过操作放到第一个，把2通过操作放到第二个。。。以此类推。但会出现一种情况，如果我们所要排的数字在最后一位，该怎么办呢？那么我们需要把倒数第三位和倒数第四位的数字插到最后一位数字的后面，然后再按照上述的操作进行。当然，如果排到第n-1个数字时，n-1在最后一位，则无法进行操作，则数组不成立。

代码如下：

#pragma GCC optimize(3)  //O2优化开启
#include<bits/stdc++.h>
using namespace std;
#define int long long
typedef long long ll;
typedef pair<int,int> PII;
const int N=998244353;
const int MX=0x3f3f3f3f3f3f3f3f; 
int n,m;
int b[1000005];
int id[1000005];
void icealsoheat(){cin>>n;vector<PII>ans;for(int i=1;i<=n;i++){cin>>b[i];id[b[i]]=i;}for(int i=1;i<n;i++){if(b[i]==i)continue;if(id[i]==n&&i==n-1){cout<<"No";return;}if(id[i]==n){ans.push_back({n-2,n-2});int xx=b[n];b[n]=b[n-1];b[n-1]=b[n-2];b[n-2]=xx;id[b[n]]=n;id[b[n-1]]=n-1;id[b[n-2]]=n-2;}if(b[i]==i)continue;ans.push_back({id[i],i-1});int r=id[i]+1;int xx=b[r];for(int j=r;j>=i+2;j--){b[j]=b[j-2];id[b[j]]=j;}b[i]=i;b[i+1]=xx;       id[b[i]]=i;id[b[i+1]]=i+1;}cout<<"Yes\n";cout<<ans.size()<<"\n";for(auto [i,j]:ans){cout<<i<<" "<<j<<"\n";}}
signed main(){ios::sync_with_stdio(false);cin.tie();cout.tie();int _yq;_yq=1;// cin>>_yq;while(_yq--){icealsoheat();}
}

C - Mex Game on Tree

这道题其实很好判断，就是在一个子树中，要保证不存在含有k的子节点，其次还要有1到k-1的节点，才算成立。并且对于Bob来说，他会想进办法把k放入树中。所以，Alice必须在第一步就获得我们需要的值。那么我们不难想到，要么最开始就有符合要求的子树，要么就是差一个数就满足上述要求的子树（这种情况Alice第一步直接放入所需要的数就可以了）

代码如下：

#pragma GCC optimize(3)  //O2优化开启
#include<bits/stdc++.h>
using namespace std;
#define int long long
typedef long long ll;
typedef pair<int,int> PII;
const int N=998244353;
const int MX=0x3f3f3f3f3f3f3f3f; 
int n,k;
int a[1000005];
int p[1000005];
void icealsoheat(){cin>>n>>k;vector<vector<int>>ve(n+5);vector<vector<int>>dp(n+5,vector<int>(1005,0));vector<int>ge(n+5,0);for(int i=2;i<=n;i++){cin>>p[i];ve[p[i]].push_back(i);}for(int i=1;i<=n;i++)cin>>a[i];bool f=0;auto dfs=[&](auto self,int x)->void{if(a[x]>=0){dp[x][a[x]]=1;}ge[x]=1;for(auto i:ve[x]){self(self,i);for(int j=0;j<=n;j++){dp[x][j]+=dp[i][j];}ge[x]+=ge[i];}if(dp[x][k]==0){int an=0;int nn=0;for(int j=0;j<=n;j++){if(j<k){if(dp[x][j])an++;}nn+=dp[x][j];}if(an==k-1&&ge[x]-nn==1){f=1;}else if(an==k&&ge[x]-nn<=1){f=1;}}};dfs(dfs,1);if(f)puts("Alice");else puts("Bob");
}
signed main(){ios::sync_with_stdio(false);cin.tie();cout.tie();int _yq;_yq=1;cin>>_yq;while(_yq--){icealsoheat();}
}

D - Smallest Vertices

参考文献：ARC162 简要题解 - syzf2222 的博客 - 洛谷博客 (luogu.com.cn)

以及你别想再给我走了！ (cnblogs.com)

从这题开始，发现自己开始力不从心了。好难好难。。。

首先，我们需要知道基本的prufer序列的一些知识：

一棵n个点的带标号生成树唯一对应一个长度为 n-2的Prufer 序列。

Prufer 序列是这样构造的：每次选出编号最小的叶子节点（没有子节点的点），将它删去，并将它相连的点加入序列中，直到进行n−2 次后剩两个点。一个点prufer 序列中出现的次数为度数-1。每个数都可能在prufer 序列的每个位置出现。

第三个结论是解决本题的关键。

对于一个子树而言，如果该子树的根节点对答案有贡献，则该子树除根节点以外的节点的数字一定要大于根节点。

一个出度为drt的节点为根的生成树数量为：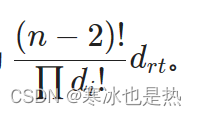

设以x为根节点的集合S，|S|为该集合的数量，集合中不存在比x更小的节点。我们还要保证集合中出度的和为|S|-1，满足上述条件才能加上此贡献。我们可以用dp去维护，dp j k ，j表示我们选了多少个数，k表示这些数的出度的和。该节点的贡献为

最后节点1的要特殊单独计算。

代码如下：

#pragma GCC optimize(3)  //O2优化开启
#include<bits/stdc++.h>
using namespace std;
#define int long long
typedef long long ll;
typedef pair<int,int> PII;
const int mod=998244353;
const int MX=0x3f3f3f3f3f3f3f3f; 
int fac[1000];
int ifac[1000];
int kuai(int a,int b){int ans=1;while(b){if(b&1)ans=ans*a%mod;b>>=1;a=a*a%mod;}return  ans%mod;
}
inline ll C(ll n, ll m) {if (n < m || n < 0 || m < 0) {return 0;} else {return fac[n] * ifac[m] % mod * ifac[n - m] % mod;}
}
int n;
int d[1000];
void icealsoheat(){cin>>n;ifac[0]=fac[0]=1;for (int i = 1; i <= 505; ++i) {fac[i] = fac[i - 1] * i % mod;}ifac[505] = kuai(fac[505], mod - 2);for (int i = 505 - 1; ~i; --i) {ifac[i] = ifac[i + 1] * (i + 1) % mod;}int res=1;for(int i=1;i<=n;i++){cin>>d[i];// if(d[i]){//     res=res*d[i]%mod;// }res=res*ifac[d[i]]%mod;}vector dp(n+5,vector<int>(505,0));dp[0][0]=1;// res=kuai(res,mod-2);int ans=0;for(int i=n;i>=2;i--){if(d[i]){for(int j=d[i];j<=n-i;j++){int xx=dp[j][j-d[i]];xx=xx*d[i]%mod*d[1]%mod;xx=xx*fac[j-1]%mod*fac[n-j-2]%mod;xx=xx*res%mod;ans=(ans+xx)%mod;}}for(int j=n-i+1;j>=0;j--){for(int k=n;k>=0;k--){if(k>=d[i]&&j){dp[j][k]=(dp[j][k]+dp[j-1][k-d[i]])%mod;}}}if(!d[i]){int xx=fac[n-2]*d[1]%mod*res%mod;ans=(ans+xx)%mod;}}int xx=fac[n-2]*d[1]%mod;xx=xx*res%mod;ans+=xx;cout<<ans%mod;}
signed main(){ios::sync_with_stdio(false);cin.tie();cout.tie();int _yq;_yq=1;// cin>>_yq;while(_yq--){icealsoheat();}
}

E - Strange Constraints

好厉害的题，我完全想不到，也看题解了好长时间，感觉长脑子了，完全没想到竟然还可以这个样子。

参考文献：AT_arc162_e [ARC162E] Strange Constraints - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

代码如下：

#pragma GCC optimize(3)  //O2优化开启
#include<bits/stdc++.h>
using namespace std;
#define int long long
typedef long long ll;
typedef pair<int,int> PII;
const int mod=998244353;
const int MX=0x3f3f3f3f3f3f3f3f; int dp[505][505][505];
int fac[10005];
int ifac[10005];
int kuai(int a,int b){int ans=1;while(b){if(b&1)ans=ans*a%mod;b>>=1;a=a*a%mod;}return ans%mod;
}
int b[10005];
inline ll C(ll n, ll m) {if (n < m || n < 0 || m < 0) {return 0;} else {return fac[n] * ifac[m] % mod * ifac[n - m] % mod;}
}
int n;
void icealsoheat(){cin>>n;fac[0]=1;for (int i = 1; i <= n; ++i) {fac[i] = fac[i - 1] * i % mod;}ifac[n] = kuai(fac[n], mod - 2);for (int i = n - 1; i>=0; --i) {ifac[i] = ifac[i + 1] * (i + 1) % mod;}for(int i=1;i<=n;i++){int x;cin>>x;b[x]++;}b[n+1]=0;int ans=0;for(int i=n-1;i>=1;i--)b[i]+=b[i+1];dp[n+1][0][0]=1;for(int i=n;i>=1;i--){for(int j=0;j*(i+1)<=n&&j<=b[i+1];j++){for(int k=0;k<=b[i+1];k++){if(dp[i+1][j][k]==0)continue;int f=1;for(int x=0;j+x<=n&&k+x*i<=b[i];x++){dp[i][j+x][k+i*x]+=dp[i+1][j][k]*C(b[i]-j,x)%mod*fac[b[i]-k]%mod*f%mod*ifac[b[i]-k-i*x]%mod;dp[i][j+x][k+i*x]%=mod;f=f*ifac[i]%mod;}}}}for(int i=0;i<=b[1];i++){ans=(ans+dp[1][i][n])%mod;}cout<<ans;
}
signed main(){ios::sync_with_stdio(false);cin.tie();cout.tie();int _yq;_yq=1;// cin>>_yq;while(_yq--){icealsoheat();}
}