支持向量机推导之r||w||=1的限制转化
很多同学肯定是学过支持向量机的,也可能大致的理解了支持向量机这个算法,我想大部分人在学习这个算法的时候,对于推导过程有一步应该是不太理解。
我先简要介绍一下SVM,SVM的核心思想在于找到一个多维空间的超平面,可以最好的将我们的样本分隔开来。
超平面大家都知道,数学表达式如下:
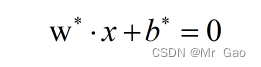
那么最好的将我们的样本分隔开来怎么解释?
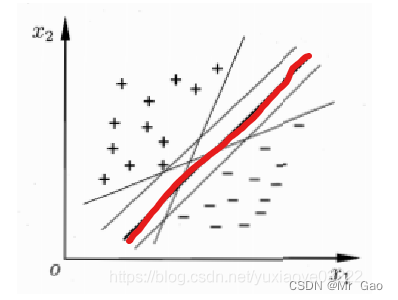
看下面一张图:
我们可以发现,有很多超平面,或者说线,都可以把我们的样本都正确的分隔开来,但如果从直观的效果靠,是不是红色的那一条是效果最好的,那么这一条怎么找到呢?
下面我们再看一个概念,样本到超平面的距离公式:
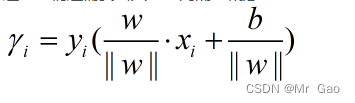
上式就是样本到超平面的距离公式,这就不推导了。
有了这个距离公式,再结合我们的常识,我们知道,当我们每次有了一个超平面,是不是可以求得每个样本到超平面的距离,那么研究者根据先验经验认为,每一个超平面求得之后呢,都会存在一个样本到超平面的最小距离,研究者们发现,如果这个最小距离越大,超平面的分类效果越好,于是得到了我们的SVM模型,即求解一个超平面,可以将样本都正确分类,且样本到超平面的最小距离最大。
由此,我们得到了支持向量机模型的数学推导:
注: 下面的 γ \gamma γ是样本到超平面的最小距离
那么就到了本次博客内容真正的核心问题了,上面的数学表达是如何转化为下面的数学表达的:
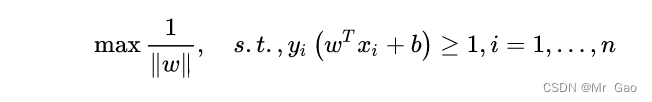
很多同学肯定看过这样的解释:

但是其实这个解释,我认为对于很多人可能不是很能看得懂,从数学推导的角度上来说,这个推到是没有说服力的,下面我来给大家推到一下:
- 先回到最开始的数学表达
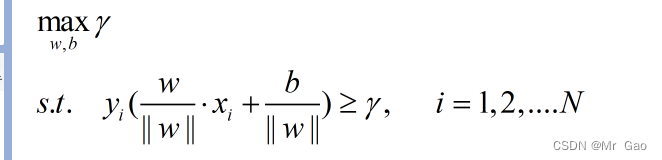
2.然后,我们可以把上述问题转化为如下问题:
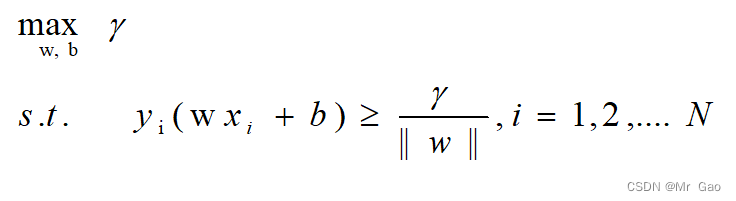
2.然后令 γ \gamma γ/||w||=1,然后就转化好了
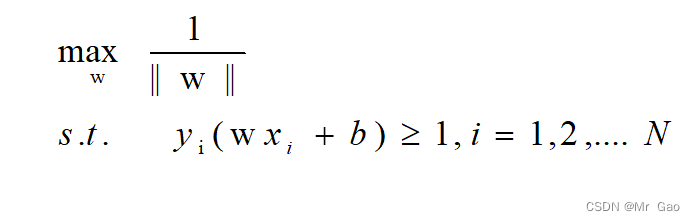
那么我们现在来探讨为什么令 γ \gamma γ/||w||=1不影响结果,令 γ \gamma γ/||w||=1其实是限制w的取值空间,也就是,现在我们取值的w满足使得 γ \gamma γ/||w||=1。w的取值空间被限制了,不再是可以随机的取值了,所以我们需要从满足条件的w中寻找最优结果。但是,这个限制再上面优化公式里其实并没有体现出来,博主再看svm求解的过程中发现,如果使用拉格朗日乘子法求解上述最优化问题,上述不等式约束的等式会被满足,也就是求得的w和b一定会满足使得 γ \gamma γ/||w||=1的情况。我觉得这是一个乌龙。只是因为我们的优化方法会自动地满足等式,也就是满足 γ \gamma γ/||w||=1,但如果优化的方法求得的结果可能不满足等式,我认为上述优化公式是不足够的。
所以我觉得真实的优化问题应该是下面这个:
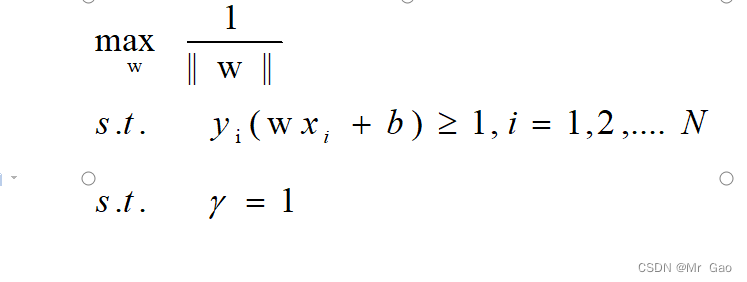
但是因为通过拉格朗日乘子法求解问题是,在忽略了下面约束等式的情况下,求得的结果却满足约束等式,也就是,没有其约束的情况求得的结果,那么其所搜索的w的集合是更大的,即包括了约束之后的w取值集合,这个时候它求解的结果却满足了等式,那么这结果一定是最优解。
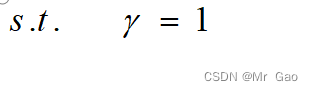
我举个例子啊:
你现在在摘桃子,一共有一百个果园,要你摘出最好吃的桃子,但是这个最好吃的桃子必须是在某个特定的果园,比如10号果园,如果你摘出最好吃的果子不在十号果园,则失败,但是你事先不知道最好吃的果子必须来自十号果园。
结果,你现在把一百个果园的果子都尝了,且你发现最好吃的果子就在10号果园。圆满的完成了任务。
大概就是这个意思,本来只想让你在10号果园找最好吃的果子,结果你去了所有的果园,结果发现最好吃的果子就在十号果园。所以SVM模型其实我觉得是一个乌龙,也可能这个被人给证明过了。