AVL树实现

目录

​编辑

一，AVL树的概念

二，实现AVL树（部分）

1.AVL树的节点

2.AVL数的插入

1.当根节点为nullptr时要执行如下代码：

2.当根节点不为nullptr时

1.当parent的_bf变为0时，parent之前的_bf的大小就是-1或者1如下：

2.当parent的平衡因子被更新为1或者-1时：

3.当parent的平衡因子更新后变成-2或者2时

三，一些其他函数

四，全部代码

一，AVL树的概念

首先我们得先知道AVL树是个啥，AVL树是个啥呢？百度一下你就知道：

在百度上的概念如上。根据AVL树的概念我们可以总结出AVL树有如下特点：

1.本身首先是一棵二叉搜索树。

2.带有平衡条件：每个结点的左右子树的高度之差的绝对值（平衡因子）最多为1。

二，实现AVL树（部分）

1.AVL树的节点

 首先我们根据AVL树的特点可以想到的AVL树节点成员有：

1.因为AVL树还是一棵二叉树，所以AVL树中必有指针left与right，而且还有一个变量表示节点值。

2.因为二AVL树需要记录高度差，所以在节点内就会有一个变量来记录高度差，这个变量便是平衡因子。并且这个变量的类型是int。

3.最后为了方便后续操作，我们的节点内还会存放一个指针叫做parent，这个节点指向当前节点的父节点。

所以写出的节点代码如下：

template <class K,class V>struct AVL_Node//节点{AVL_Node(pair<K,V>& key):parent(nullptr),_left(nullptr),_right(nullptr),_bf(0),_key(key){}AVL_Node<K, V>* parent;//父节点指针AVL_Node<K, V>* _left;//左孩子指针AVL_Node<K, V>* _right;//右孩子指针int _bf;//平衡因子pair<K, V>_key;//val};

2.AVL数的插入

AVL树的插入是我们这次实现的重头戏，在插入时要理解的重点内容便是：

1.插入时的旋转。

2.平衡因子的调整。

现在先来写在旋转前的代码：

1.当根节点为nullptr时要执行如下代码：
if (_root == nullptr)//当根节点为空时
{_root = new AVL_Node<K, V>(key);
}
2.当根节点不为nullptr时

1.先找到插入位置：

AVL_Node<K, V>* cur = _root;
AVL_Node<K, V>* parent = cur;
while (cur)
{
if (key < cur->_key)
{parent = cur;cur = cur->_left;
}
else if (key > cur->_key)
{parent = cur;cur = cur->_right;
}
else
{return false;
}
}

这段寻找插入位置的代码和二叉搜索树的代码相同。

2.找到插入位置以后便开始进行插入

cur = new AVL_Node<K, V>(key);
if (key.first > parent->_key.first)
{parent->_right = cur;
}else
{parent->_left = cur;
}cur->_parent = parent;//更新父节点

3.调整上一个节点的平衡因子。依据：_bf = 右节点的高度--左节点的高度

所以当我插入左边时：

if (cur == parent->_left)//左边添加节点，parent的_bf减1
{parent->_bf--;
}

当我插入右边时：

else if (cur == parent->_right)//右边添加节点，parntt的高度加1
{parent->_bf++;
}

4.根据父节点的_bf的大小来决定是否需要往上调整

1.当parent的_bf变为0时，parent之前的_bf的大小就是-1或者1如下：

其实我的parent变成0以后AVL树的高度下降，所以对我的其它节点的平衡因子的大小是没有什么影响的，所以在这种情况下我便可以直接退出：

if (parent->_bf == 0)//子树高度不变不影响整棵树高度
{break;
}
2.当parent的平衡因子被更新为1或者-1时：

能变更新成这种情况，那我之前的平衡因子一定为0了。这时候，我整棵树的高度肯定是增加了，所以平衡因子必须改变所以代码如下:

else if (parent->_bf == 1 || parent->_bf == -1)//子树高度变了，但是在接受范围内，节点的平衡因子要做调整
{cur = parent;parent = parent->_parent;
}

这段代码是不全的，这里只展示了节点向上调整的操作，如果想看整段代码请往后看。

3.当parent的平衡因子更新后变成-2或者2时

这个时候就发生异常了，这个时候就要开始旋转了。这个时候的旋转又分为四种：

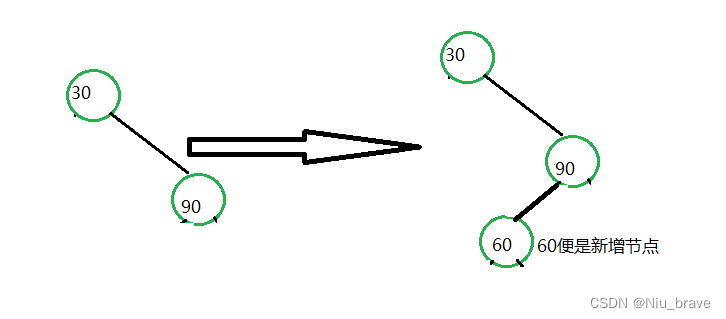
1.单纯的右边高

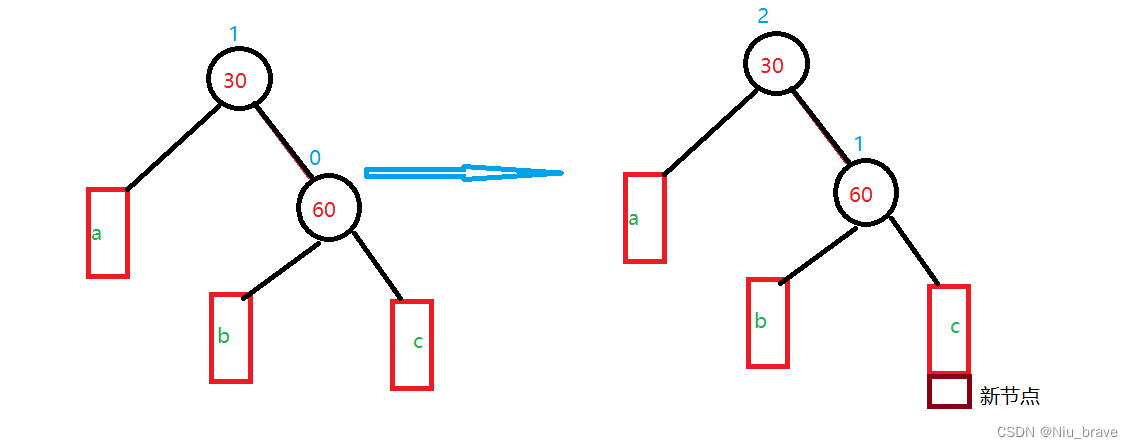
如以下情况：

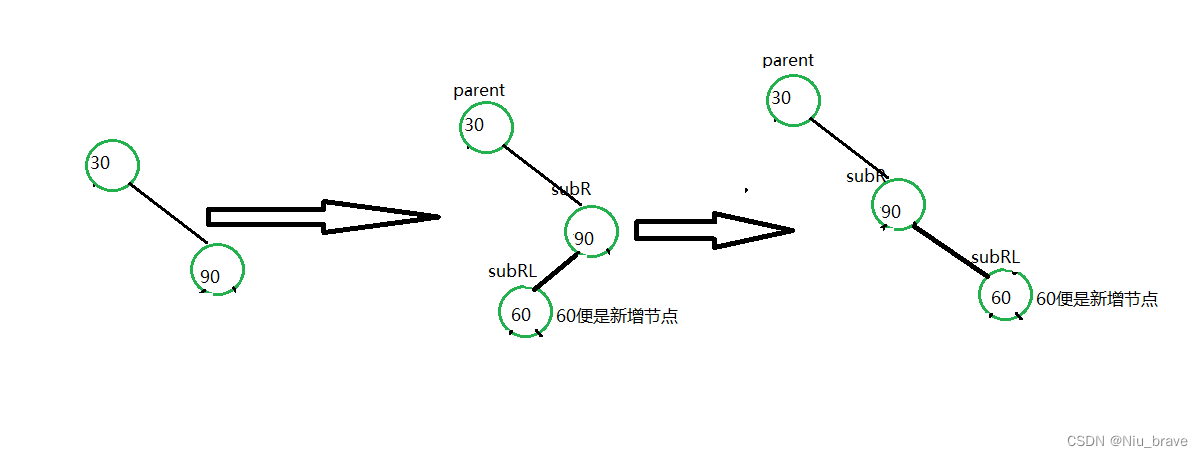
可以看到在插入新的节点以后，树的高度发生了变化并且都是右边的高度高且出现了异常情况。所以这个时候就要发生左旋来调整高度，示意图如下：

根据这个过程写出如下代码：

void Leftuniflex(AVL_Node<K, V>* parent){//记录要旋转的节点AVL_Node<K, V>* subR = parent->_right;AVL_Node<K, V>* subRL = subR->_left;//旋转parent->_right = subRL;subR->_left = parent;//更新父节点AVL_Node<K, V>* ppNode = parent->_parent;parent->_parent = subR;if (subRL)subRL->_parent = parent;if (parent == _root){_root = subR;}subR->_parent = ppNode;//更新平衡因子parent->_bf = subR->_bf = 0;}

因为在示意图里没有显示父节点的更新，所以在这里要注意对于父节点的更新。

2.单纯的左边高

如下情况：

看到这个示意图是否有一种似曾相识的感觉呢？其实单纯的左边高的旋转操作方法和单纯右边高的操作方法一样，只不过旋转的方向改变了。根据示意图写出代码如下：
 

void Rightuniflex(AVL_Node<K, V>* parent){//旋转AVL_Node<K, V>* subL = parent->_left;AVL_Node<K, V>* subLR = subL->_right;parent->_left = subLR;subL->_right = parent;//更新父节点AVL_Node<K, V>* ppNode = parent->_parent;parent->_parent = subL;if (subLR)subLR->_parent = parent;if (parent == _root){_root = subL;}subL->_parent = ppNode;//更新平衡因子parent->_bf = subL->_bf = 0;}

3.右边整体高但是局部矮

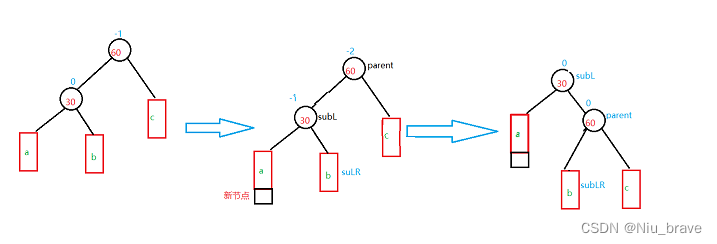
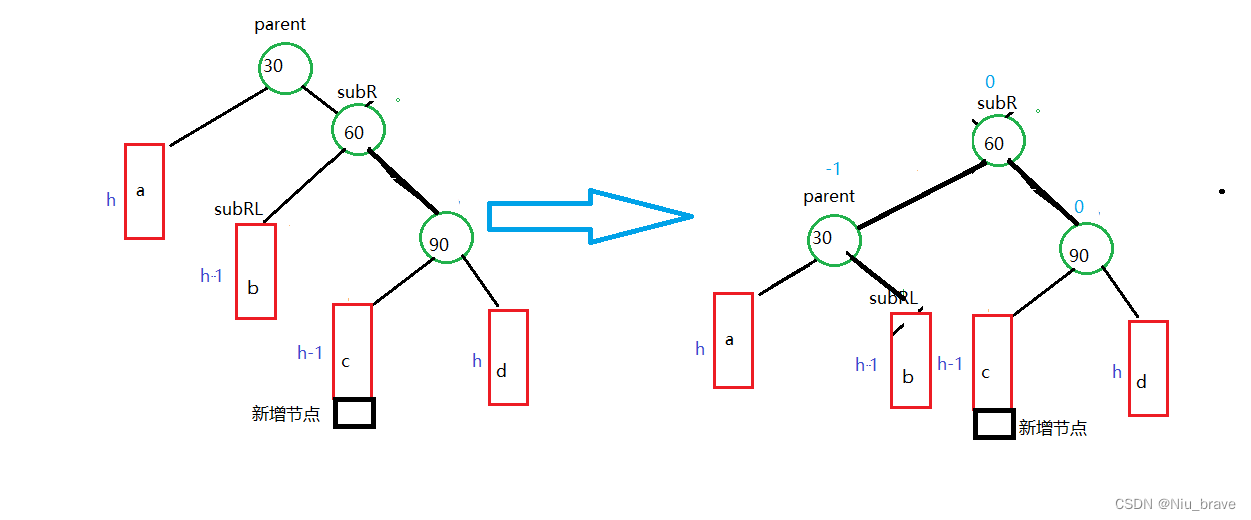
解决方法：1.将整棵AVL树通过右单旋调整成单纯的右边高然后再将整棵树通过左单旋调整成平衡的AVL树。比如如以下情况：

一，新增节点插入到60的右节点b处，此时60的_bf为-1

在这种情况下，首先便要以90这个节点为parent进行右单旋让整棵树变成单纯的右边高。如下图所示：

在转化为单纯的右边高以后，便可以执行第二步了。第二步的操作便是和左旋操作是一样的，如图所示：

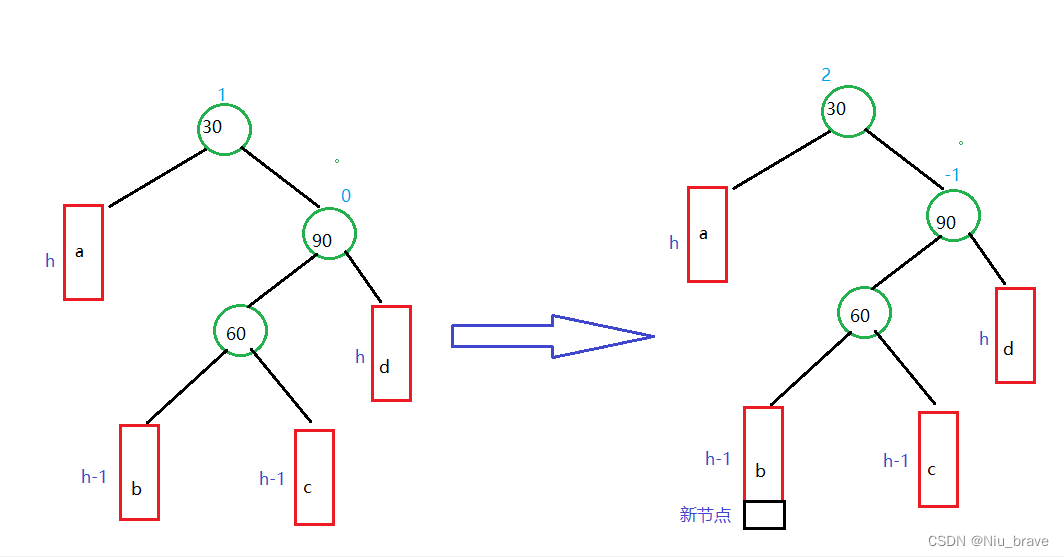
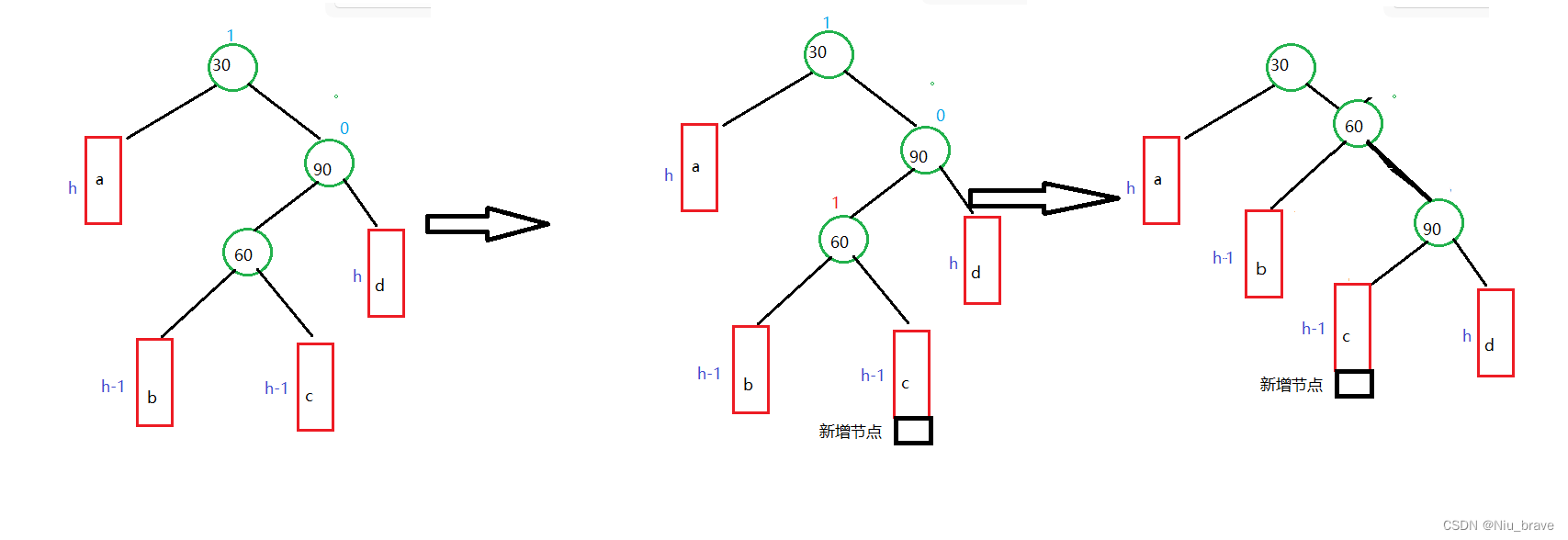
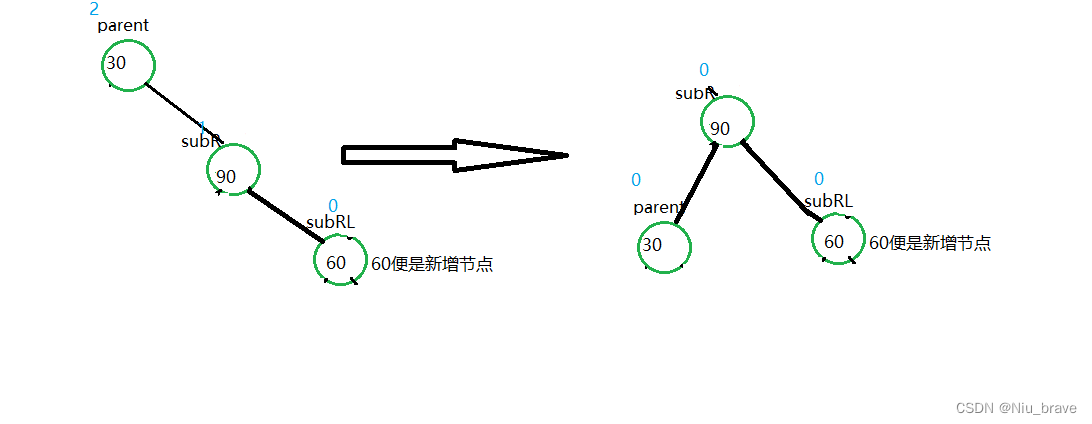
二，新增节点插入到60的右节点c处，此时60的_bf为1

画出示意图如下：

然后还是一样的操作将这棵树变成单纯的右边高：

然后继续执行第二步，也是单纯的左旋操作：

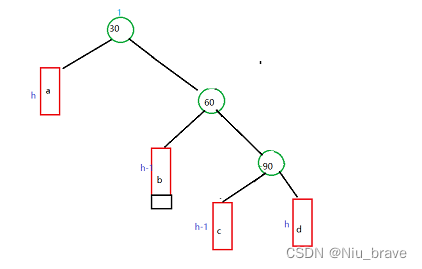
三，当h为0时，新增节点为60。此时60的_bf = 0

在这个时候还是一样的操作：先变成单纯的右边高

然后再操作：

再右边整体高，局部左边高的节点插入情况便是以上三种。其实这些情况的旋转操作都是一样的但是对应的平衡因子_bf的更新是不一样的。

根据以上情况写出代码如下：

//右左双旋void RLuniflex(AVL_Node<K, V>* parent){AVL_Node<K, V>* subR = parent->_right;AVL_Node<K, V>* subRL = subR->_left;int bf = subRL->_bf;Rightuniflex(subR);//先局部右旋Leftuniflex(parent);//再整体左旋//更新平衡因子if (bf == 0)//subRL自己就是新增{parent->_bf = subR->_bf = subRL->_bf = 0;}else if (bf == -1){subR->_bf = 1;parent->_bf = subRL->_bf = 0;}else if (bf == 1){parent->_bf = -1;subRL->_bf = subR->_bf = 0;}else{assert(false);}}

4.当左边整体高但是右边局部高时：

在这种情况下的分析方法和《当右边整体高但是左边局部高》的分析方法相同。也分为三步：

1.现局部左旋让AVL树变成单纯的左边高。

2.再整体右旋调整树的平衡。

3.调整平衡因子。

分析方法和上述代码相同，在这里就直接写代码了：

//左右双旋(狗日的平衡因子，让我搞了半天，哭了)void LRuniflex(AVL_Node<K, V>* parent){AVL_Node<K, V>* subL = parent->_left;AVL_Node<K, V>* subLR = subL->_right;int bf = subLR->_bf;Leftuniflex(subL);//先局部左旋Rightuniflex(parent);//再整体右旋//更新平衡因子if (bf == 0)//subRL自己就是新增{parent->_bf = subL->_bf = subLR->_bf = 0;}else if (bf == -1){subL->_bf = 0;parent->_bf = 1;subLR->_bf = 0;}else if (bf == 1){parent->_bf = 0;subLR->_bf = 0;subL->_bf = -1;}else{assert(false);}}

兄弟们在写代码时千万不要和我一样粗心，找bug找了好久！！！！

三，一些其他函数

1.中序遍历函数

void Inorder()
{_Inorder(_root);
}

void _Inorder(AVL_Node<K, V>* root)
{if (root == nullptr){return;}_Inorder(root->_left);cout << root->_key.first << " ";_Inorder(root->_right);
}

记住，AVL树的中序遍历也是一个有序的数列。

2.判断平衡的函数

int Height(AVL_Node<K, V>* root){if (root == nullptr){return 0;}int L = Height(root->_left);int R = Height(root->_right);return L > R ? L + 1 : R + 1;}bool _Isblance(AVL_Node<K, V>* root){if (root == nullptr){return true;}int R = Height(root->_right);int L = Height(root->_left);int bf = root->_bf;if (R - L!=bf){cout << "R-L:" << R - L << endl;cout << root->_key.first << "->" << root->_bf <<"平衡因子异常" << endl;return false;}return (abs(R-L)<2)&& _Isblance(root->_left) && _Isblance(root->_right);}

四，全部代码

#include<iostream>
#include<assert.h>
using namespace std;
using std::pair;namespace AVL
{template <class K,class V>struct AVL_Node//节点{AVL_Node(pair<K,V>& key):_parent(nullptr),_left(nullptr),_right(nullptr),_bf(0),_key(key){}AVL_Node<K, V>* _parent;AVL_Node<K, V>* _left;AVL_Node<K, V>* _right;int _bf;pair<K, V>_key;};template <class K, class V>class AVL_Tree{public:bool insert( pair<K, V> key){if (_root == nullptr)//当根节点为空时{_root = new AVL_Node<K, V>(key);}else//当根节点不为空时{AVL_Node<K, V>* cur = _root;AVL_Node<K, V>* parent = cur;while (cur){if (key.first < cur->_key.first){parent = cur;cur = cur->_left;}else if (key.first > cur->_key.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new AVL_Node<K, V>(key);if (key.first > parent->_key.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent){if (cur == parent->_left)//左边添加节点，parent的高度减1{parent->_bf--;}else if (cur == parent->_right)//右边添加节点，parent的高度加1{parent->_bf++;}if (parent->_bf == 0)//子树高度不变不影响整棵树高度{break;}else if (parent->_bf == 1 || parent->_bf == -1)//子树高度变了，但是在接受范围内，节点的平衡因子要做调整{cur = cur->_parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//Inorder();//出现异常该旋转了//单纯右边高，发生左单旋if (parent->_bf == 2 && cur->_bf == 1){Leftuniflex(parent);}//单纯左边高，发生右单旋else if (parent->_bf == -2 && cur->_bf == -1){Rightuniflex(parent);}//右边整体高，局部矮else if (parent->_bf == 2 && cur->_bf == -1){RLuniflex(parent);}//左边整体高，局部矮else if (parent->_bf == -2 && cur->_bf == 1){LRuniflex(parent);}else{assert(false);}break;}else{assert(false);}}}return true;}void Leftuniflex(AVL_Node<K, V>* parent){AVL_Node<K, V>* subR = parent->_right;AVL_Node<K, V>* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;//更新父节点AVL_Node<K, V>* ppNode = parent->_parent;parent->_parent = subR;if (subRL)subRL->_parent = parent;if (parent == _root){_root = subR;}else{if (parent == ppNode->_left){ppNode->_left = subR;}else{ppNode->_right = subR;}}subR->_parent = ppNode;//更新平衡因子parent->_bf = subR->_bf = 0;}void Rightuniflex(AVL_Node<K, V>* parent){//旋转AVL_Node<K, V>* subL = parent->_left;AVL_Node<K, V>* subLR = subL->_right;parent->_left = subLR;subL->_right = parent;//更新父节点AVL_Node<K, V>* ppNode = parent->_parent;parent->_parent = subL;if (subLR)subLR->_parent = parent;if (parent == _root){_root = subL;}else{if (parent == ppNode->_left){ppNode->_left = subL;}else{ppNode->_right = subL;}}subL->_parent = ppNode;//更新平衡因子parent->_bf = subL->_bf = 0;}//右左双旋void RLuniflex(AVL_Node<K, V>* parent){AVL_Node<K, V>* subR = parent->_right;AVL_Node<K, V>* subRL = subR->_left;int bf = subRL->_bf;Rightuniflex(subR);//先局部右旋Leftuniflex(parent);//再整体左旋//更新平衡因子if (bf == 0)//subRL自己就是新增{parent->_bf = subR->_bf = subRL->_bf = 0;}else if (bf == -1){subR->_bf = 1;parent->_bf = subRL->_bf = 0;}else if (bf == 1){parent->_bf = -1;subRL->_bf = subR->_bf = 0;}else{assert(false);}}//左右双旋(狗日的平衡因子，让我搞了半天，哭了)void LRuniflex(AVL_Node<K, V>* parent){AVL_Node<K, V>* subL = parent->_left;AVL_Node<K, V>* subLR = subL->_right;int bf = subLR->_bf;Leftuniflex(subL);//先局部左旋Rightuniflex(parent);//再整体右旋//更新平衡因子if (bf == 0)//subRL自己就是新增{parent->_bf = subL->_bf = subLR->_bf = 0;}else if (bf == -1){subL->_bf = 0;parent->_bf = 1;subLR->_bf = 0;}else if (bf == 1){parent->_bf = 0;subLR->_bf = 0;subL->_bf = -1;}else{assert(false);}}void Inorder(){_Inorder(_root);}void Isblance(){_Isblance(_root);}private:void _Inorder(AVL_Node<K, V>* root){if (root == nullptr){return;}_Inorder(root->_left);cout << root->_key.first << " ";_Inorder(root->_right);}int Height(AVL_Node<K, V>* root){if (root == nullptr){return 0;}int L = Height(root->_left);int R = Height(root->_right);return L > R ? L + 1 : R + 1;}bool _Isblance(AVL_Node<K, V>* root){if (root == nullptr){return true;}int R = Height(root->_right);int L = Height(root->_left);int bf = root->_bf;if (R - L!=bf){cout << "R-L:" << R - L << endl;cout << root->_key.first << "->" << root->_bf <<"平衡因子异常" << endl;return false;}return (abs(R-L)<2)&& _Isblance(root->_left) && _Isblance(root->_right);}AVL_Node<K, V>* _root = nullptr;};}

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/194948.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

前端面试：如何实现并发请求数量控制？

前端面试：如何实现并发请求数量控制？

题目&#xff1a;实现一个并发请求函数concurrencyRequest(urls, maxNum) 要求如下&#xff1a; 要求最大并发数 maxNum;每当有一个请求返回&#xff0c;就留下一个空位&#xff0c;可以增加新的请求;所有请求完成后&#xff0c;结果按照 urls 里面的顺序依次打出&#xff1b;…
阅读更多...
C++初阶-内存管理

C++初阶-内存管理

内存管理 一、C/C内存分布二、C语言中动态内存管理方式&#xff1a;malloc/calloc/realloc/free三、C内存管理方式new/delete操作内置类型new和delete操作自定义类型 四、operator new与operator delete函数operator new与operator delete函数 五、new和delete的实现原理内置类…
阅读更多...
论文-分布式-拜占庭将军问题

论文-分布式-拜占庭将军问题

目录 0-前言 1-导引 2-不可能性 3将军(1叛徒)问题不存在解/不能达成共识 少于3m1个将军(有m个叛徒)不存在解/不能达成共识 精确一致性与近似一致性是同等困难的 3-使用口头消息的解 “口头消息”的含义 OM(m)算法的步骤 OM(m)算法的正确性推导 4-使用签名消息情况下…
阅读更多...
054-第三代软件开发-信号槽

054-第三代软件开发-信号槽

第三代软件开发-信号槽 文章目录 第三代软件开发-信号槽项目介绍信号槽实现原理与MFC消息映射机制区别Qt信号槽机制的优缺点 关键字&#xff1a; Qt、 Qml、 关键字3、 关键字4、 关键字5 项目介绍 欢迎来到我们的 QML & C 项目&#xff01;这个项目结合了 QML&#x…
阅读更多...
内容运营策略：个性化推荐

内容运营策略：个性化推荐

一、推荐系统流程 典型的推荐系统包括3个部分&#xff0c;即召回层&#xff08; Recall )、排序层&#xff08; Rank )和重排层&#xff08; ReRank )。 1&#xff0e;召回层&#xff08; Recall ) 召回层主要是从全量库中首先获取用户可能感兴趣的候选集&#xff0c;是推荐系…
阅读更多...
Pytest自动化测试框架：mark用法---测试用例分组执行

Pytest自动化测试框架：mark用法---测试用例分组执行

pytest中的mark&#xff1a; mark主要用于在测试用例/测试类中给用例打标记(只能使用已注册的标记名)&#xff0c;实现测试分组功能&#xff0c;并能和其它插件配合设置测试方法执行顺序等。 如下图&#xff0c;现在需要只执行红色部分的测试方法&#xff0c;其它方法不执行&am…
阅读更多...
pytest测试框架介绍(1)

pytest测试框架介绍(1)

又来每天进步一点点啦~~~ 一、Pytest介绍&#xff1a; pytest 是一个非常成熟的全功能的Python测试框架&#xff1b; pytest 简单、灵活、易上手&#xff1b; 支持参数化 能够支持简单的单元测试和复杂的功能测试&#xff0c;可以做接口自动化测试&#xff08;pytestrequests&…
阅读更多...
谈谈一个IT杂家的职业生涯规划，你的护城河被AI 攻破了么？

谈谈一个IT杂家的职业生涯规划，你的护城河被AI 攻破了么？

文章大纲 未来AI领域的专家是深度学习老中医数据为什么不断的在变化&#xff1f;炼金术(Alchemy)AI“老中医”的经验难以复制 AIGC 还未能克服的难点&#xff1a;忽然的惊喜与价值观对齐失控既是智能获得突破的重要原因&#xff0c;又是智能突破所不可避免的伴生结果大模型在泛…
阅读更多...
Google Earth Engine（GEE）操作

Google Earth Engine（GEE）操作

地理信息网站 Eatrth Explorer操作界面 在研究中&#xff0c;我们常需要遥感数据。在下面的网站中&#xff0c;可以得到遥感数据。 EarthExplorer (usgs.gov)https://earthexplorer.usgs.gov/登陆网站&#xff1a; 通常&#xff0c;在Additional Criteria中&#xff0c;可以…
阅读更多...
SpringBoot——入门及原理

SpringBoot——入门及原理

SpringBoot用来简化Spring应用开发&#xff0c;约定大于配置&#xff0c;去繁从简&#xff0c;是由Pivotal团队提供的全新框架。其设计目的是用来简化新Spring应用的初始搭建以及开发过程。该框架使用了特定的方式来进行配置&#xff08;有特殊需求可以添加自己的配置覆盖默认配…
阅读更多...
用户增长模型：3A3R策略模型

用户增长模型：3A3R策略模型

一、概述 A - A - A - R - R - R 增长模型&#xff0c;即3A3R策略模型&#xff0c;由海盗模型演变而来&#xff0c;是目前使用最多、适用范围最广的增长策略模型。原始的海盗模型由 Acquisition &#xff08;获客&#xff09;、 Activation &#xff08;活跃&#xff09;、 Re…
阅读更多...
接口自动化测试很难吗？来看看这份超详细的教程！

接口自动化测试很难吗？来看看这份超详细的教程！

接口自动化测试框架目的 测试工程师应用自动化测试框架的目的: 增强测试脚本的可维护性、易用性(降低公司自动化培训成本&#xff0c;让公司的测试工程师都可以开展自动化测试)。 以下框架以微信公众平台开放文档实战 地址&#xff1a;https://developers.weixin.qq.com/doc…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023