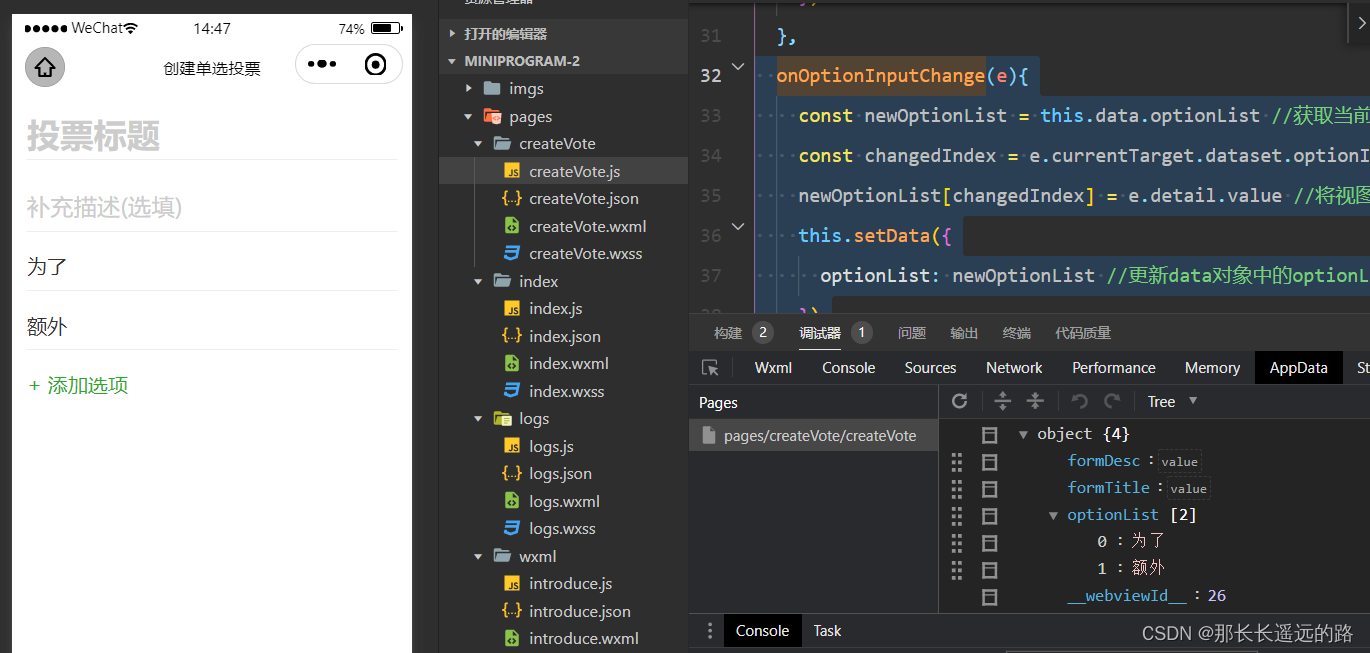
假设函数定义
假设函数,猜一个 x->y 的类型,比如 y = ax + b,随后监督学习的任务就是找到误差最低的 a 和 b 参数
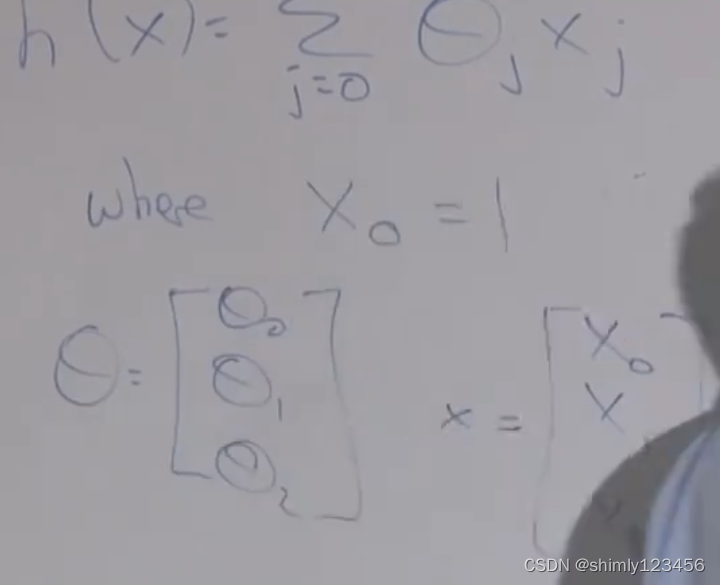
有时候我们可以定义 x0 = 1,来让假设函数的整个表达式一致统一

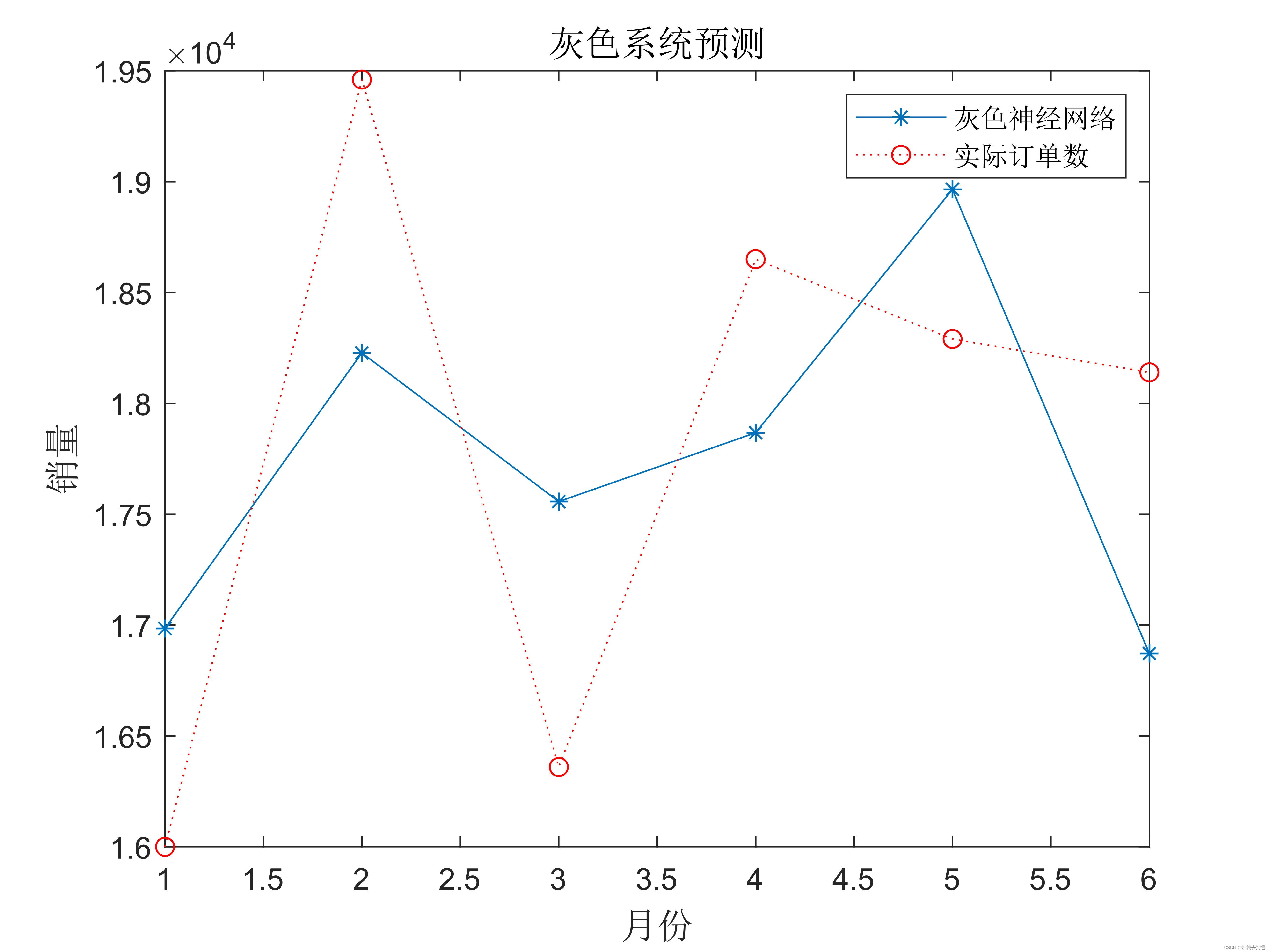
如上图是机器学习中的一些术语
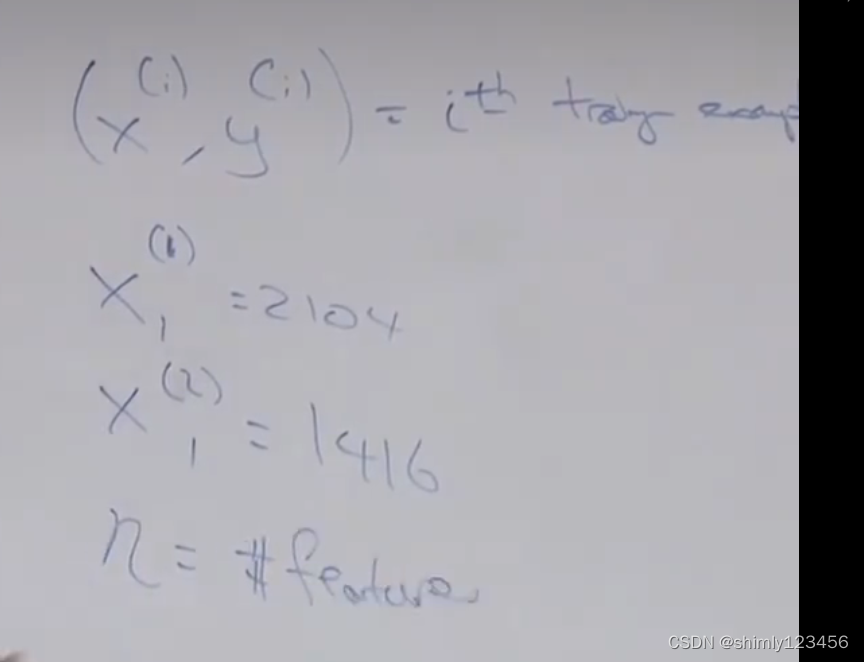
额外的符号,使用 (xi, yi) 表示第 i 个样本
n 表示特征数量 (在房屋价格预测问题中,属性/特征有两个:房子面积和卧室数量,因此这里 n = 2)
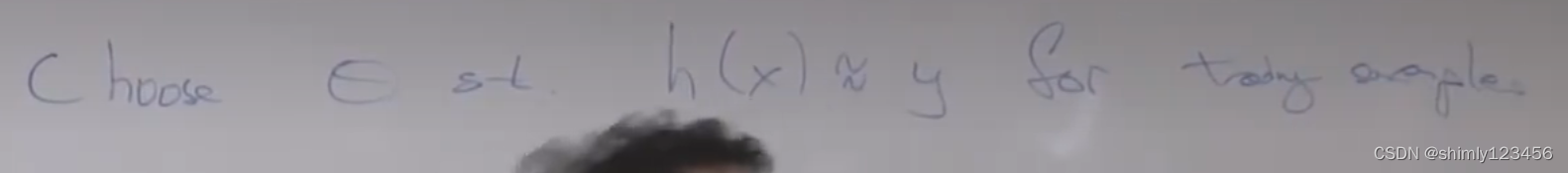
监督学习的过程就是选择合适的参数,来让假设函数的输出和样本输出相近(针对训练集)
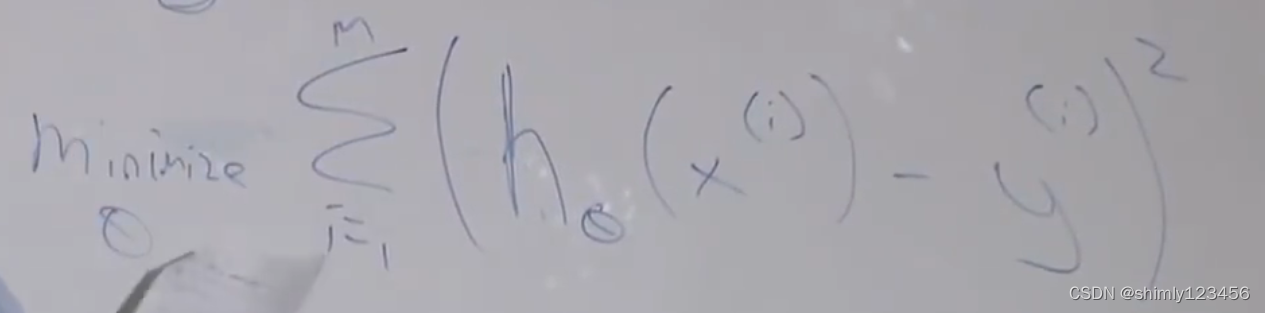
房屋预测案例中的目标函数,最小化误差平方和

我们通常会在目标函数旁边放个 1/2,这是为了后边简化求导计算
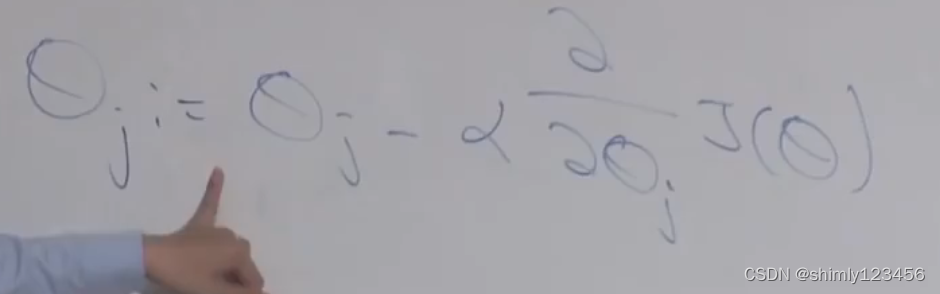
我们通常使用梯度下降法来选取更加合适的 theta参数 来优化目标函数,如上图是梯度下降法中的 “baby step”
这里的 阿尔法 就是学习速率
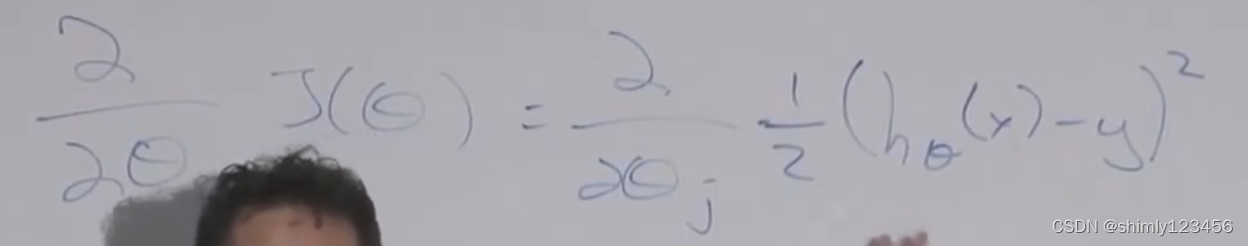
如图,是对目标函数的求导 (由于对几个项的和求导,等于它们的导数和,所以这里我们先不 care 那个 sum(sigma) 符号)
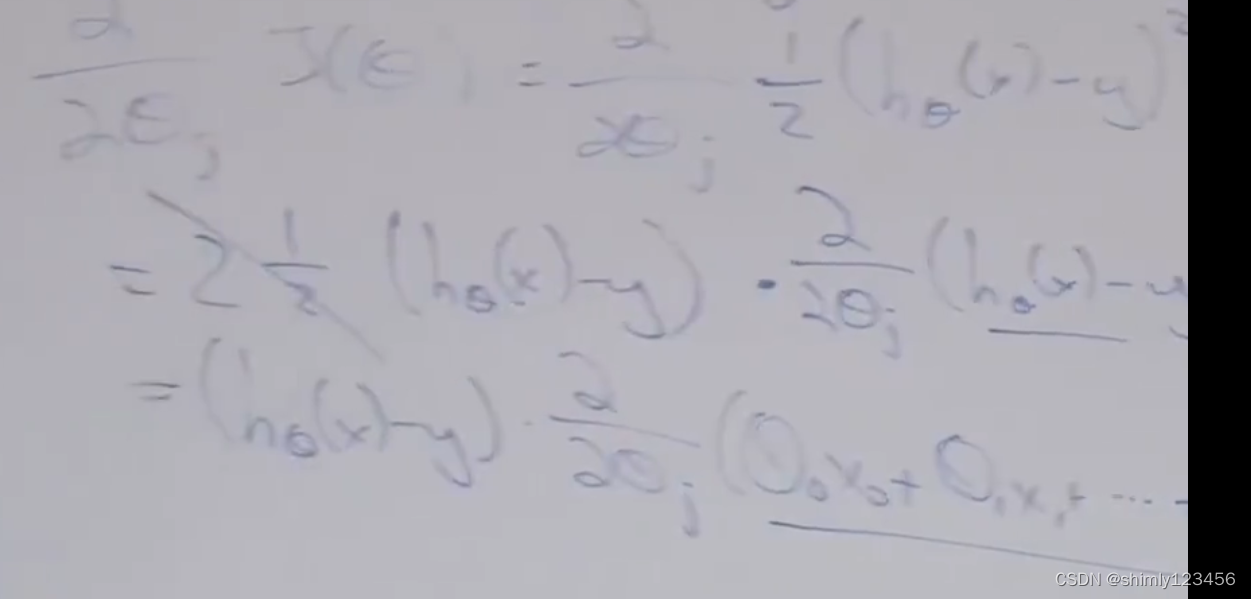
如图,是对求导公式的后续转换

如图,这是对目标函数求导的最终公式的其中一项 (这里只对 theta_j 求导)
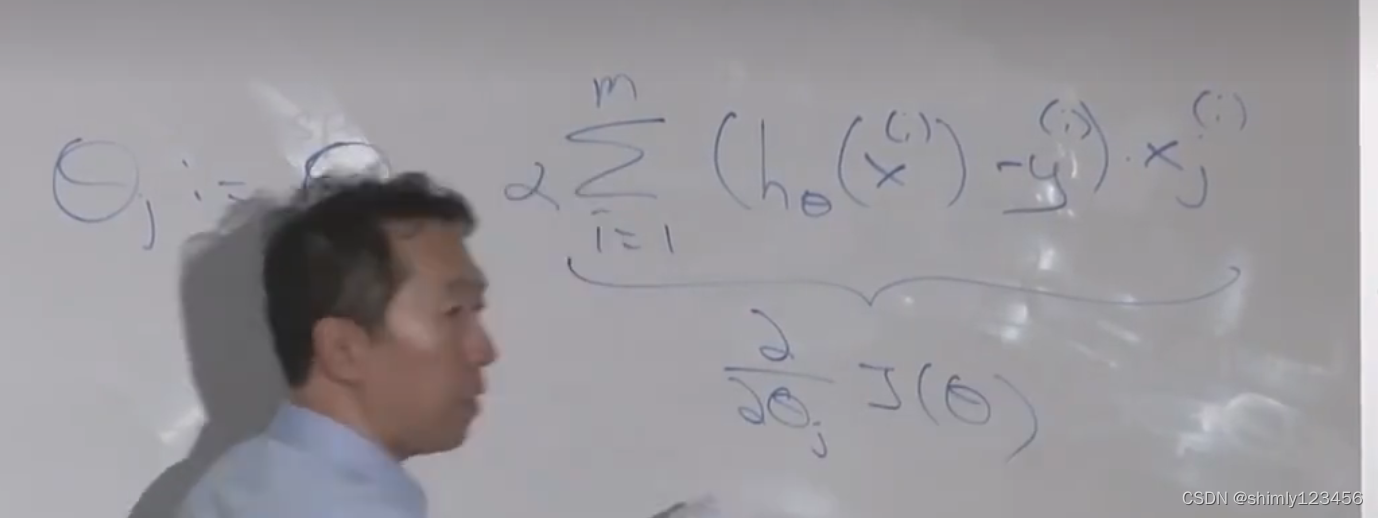
这也是最后统合得到的求导公式,对每一个样本 i 进行针对 theta_j 的求导
接下来要做的就是,重复 updating theta_j,直到目标函数收敛

由于我们的目标函数对于每个 theta_j 都是二次函数,所以这是一个凸函数,它是一个大碗,它只有一个全局最优
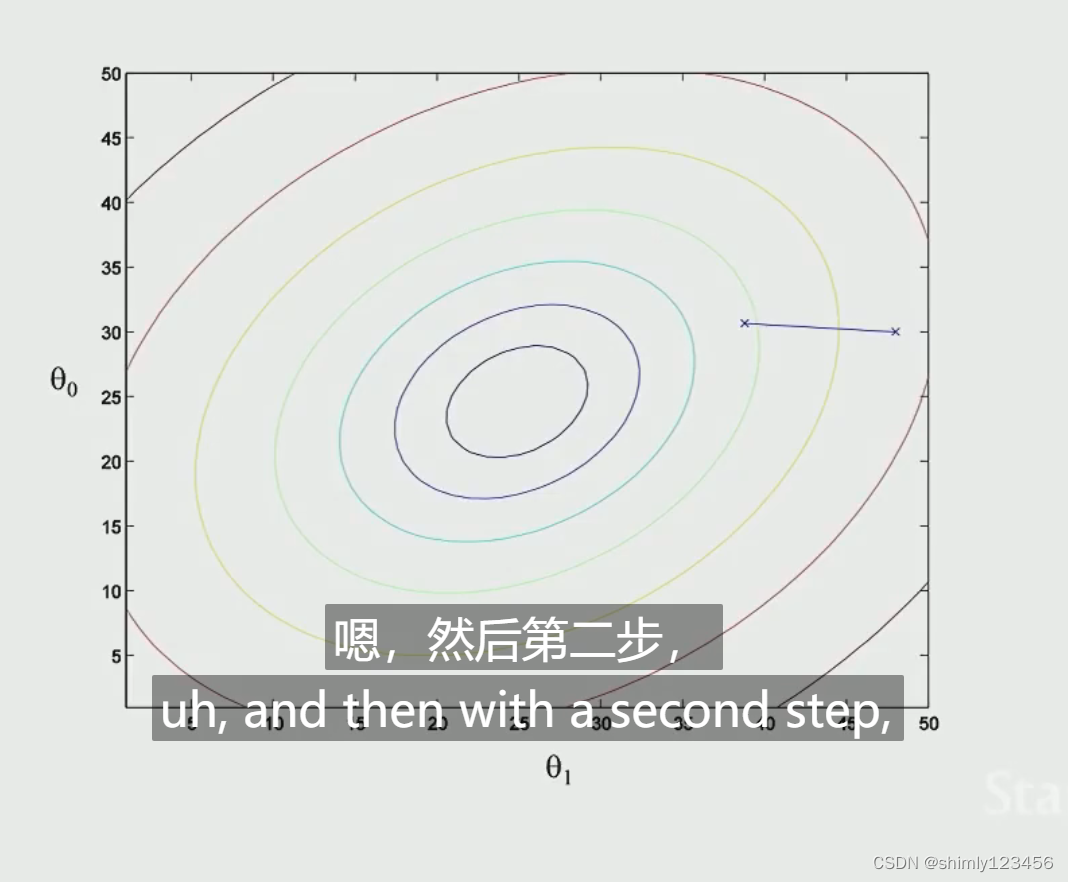
也可以用等高线图来表示
运用高中的一些数学知识,你会发现,最陡的防线和等高线(椭圆)的切线是90度
调试学习率的一些经验:
如果你发现目标函数在增加而不是减少,那通常说明学习率太大了(超调)
可以尝试 O1, O2, O4, O8 尝试不同的值
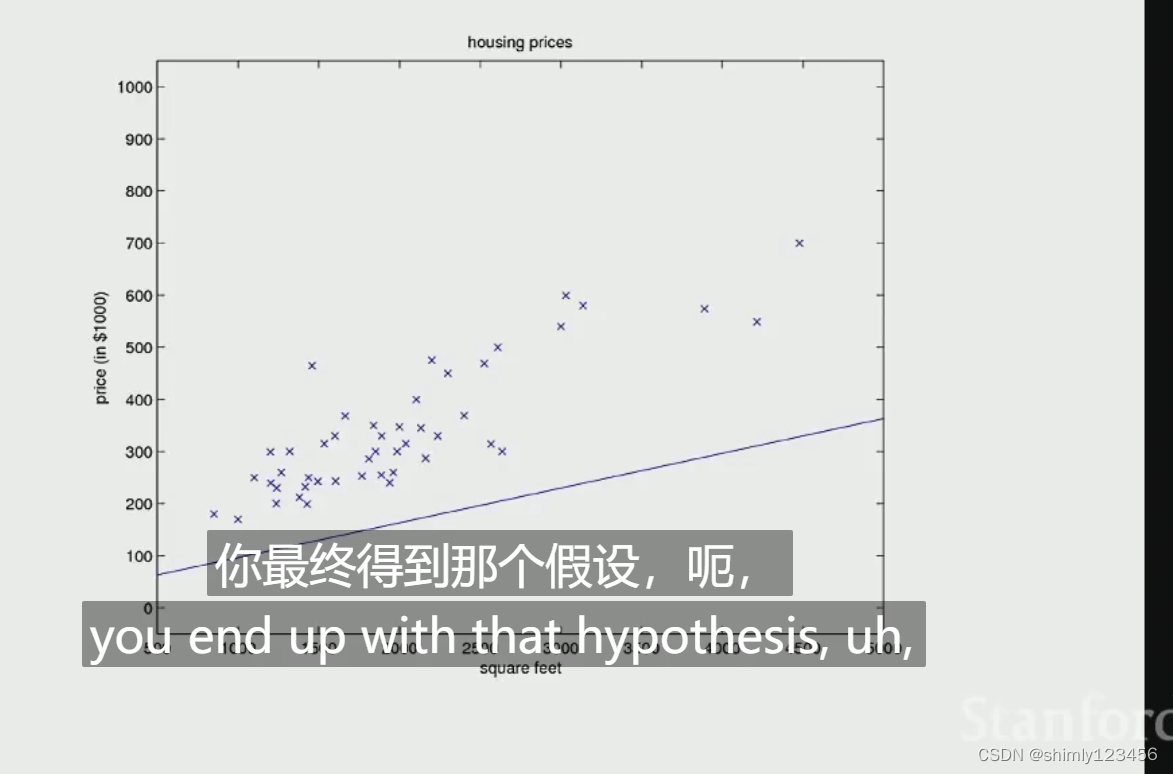
另一种可视化学习过程的方式是,看到曲线(假设函数)一点点变化
刚刚提到的机器学习方法中,梯度下降需要用到训练集中所有的样本,来计算梯度(所以也叫批量梯度下降法)。在训练集很大的情况下,这会变得昂贵,因此我们需要做些改变

另一种快得多的方式是随机梯度下降法,它遍历每一个样本 i,随后针对这单个样本对所有的 theta_j 做梯度下降
(原先的方法中,我们每做一个 tiny step 都需要扫描一次所有的样本;而 SGD 中,我们每走一个 step 只需要扫描一个样本,因此快得多)
一个更直观的解释 SGD 的方式是,一开始我的 theta 参数是随机的,然后我看到了第一个样本 x1,随后我针对这个 x1 修改的我 theta,接着我看到了 x2,我再针对 x2 修改我的 theta。在等高线图中,你可能会看到,参数并没有沿着 90 度的方向下降,而是以一种更曲折的方式下降
SGD 通常不会收敛,它会振荡
还有一种下降方法是“小批量梯度下降法”,一次遍历100个样本
还有一种实践中的方法(一点点减少学习速率)
线性回归没有局部最优(在它的目标函数是误差平方和时),只有全局最优。所以,实际上你可以使用一个矩阵去表示它的参数,求cost function(目标函数)对于 参数矩阵的求导,随后让导数 = 0,求这个位置上的导数矩阵,即可直接得到全局最优解。这也叫做正态方程,这个方法仅适用于线性回归

根据吴恩达的推导,正态方程,也就是最终最优的 theta 可以通过这么一个公式求出来
如果发现 X 不可逆,那么通常意味着有多余的 features,你有某些 features 是线性相关的,你可以使用伪逆,或者找出哪些特征是线性相关的
关于怎么选择学习率:这非常依赖经验,通常我们尝试许多个不同的值,然后选择一个