基于粒子群优化算法的分布式电源选址与定容【多目标优化】【IEEE33节点】（Matlab代码实现）-编程知识

基于粒子群优化算法的分布式电源选址与定容【多目标优化】【IEEE33节点】（Matlab代码实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

1.1 目标函数

2.2 约束条件

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

分布式电源接入配电网，实现就地消纳，可以提高新能源的利用率、提高电能质量和降低系统网损。然而接入点位置和电源的容量的差异对配电网的影响不同，如果位置和容量不合适，可能会导致系统中某处的电压越限、总系统的网损增加。因此在电源规划阶段分析分布式电源接入点的位置和容量十分有必要。分布式电源接入点和接入容量的选择问题是一个非线性、多变量、多约束的问题。目前国内外关于这方面的研究主要集中在两个方面，一是数学模型的优化，二是模型求解和算法优化。已有的诸多研究取决与分布式电源的种类，即是否只向电网提供有功功率。而且很多算法

利用准确的损耗公式，计算时需要准确阻抗矩阵和雅可比矩阵，计算效率低。因此针对不同大小、复杂性，有待于找出一种适用于所有情况的方法。本文提出了一种确定分布式电源的最佳容量和位置的分析，该方法计算效率高，适用范围广。

1.1 目标函数

(1)以系统有功网损最小和电压偏差最小建立多目标优化数学模型，其目标函数为：

式中：N为支路总数；Pi和Qi分别为第i条支路的有功与无功功率；Ui为第i条支路的末端节点电压；Ri为第i条支路的电阻；ki为第i条支路的开关状态，0代表断开，1代表闭合；f1为总有功损耗。t为节点编号；k为节点总数；Uts、UtN分别表示第t个节点的实际电压与额定电压；f2表示电压偏移量。

(2)光伏消纳量增加通常也会引起网络损耗的增加，为真实体现系统中光伏的有效消纳，在此将光伏实际消纳量与系统网络损耗的差值定义为有效消纳量Ec如下：

式中：T 为重构周期时段数；H为接入分布式光伏电源的节点数；PC(i，t )为节点i在t时段实际消纳的分布式光伏有功功率；K为配电网中的闭合支路数；Ptk、Qtk和Utk分别为支路k 在t时段的有功功率、无功功率和电压；rk为支路k的电阻。

光伏设备出力PPV如下：

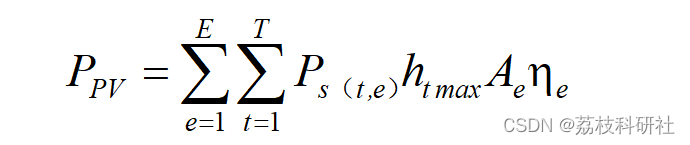
其中，E 为光伏电池板数；PS(t，e )为第e个光伏电池板在t时段实际可发功率的标幺值；htmax为在t时段光照强度的最大值；Ae、ηe分别为第e个光伏电池板的面积和光电转换效率。

为了表征有效消纳量与光伏设备出力的关系，并使优化模型更为简便，将光伏设备出力和光伏有效消纳量比值定义为函数f3。则f3越小证明消纳效果越好，最小化目标函数为：

优化调度模型的目标函数F由3部分组合而成，如下式所示：

2.2 约束条件

优化的目标是得到5个接入节点和对应接入的容量，平衡节点1不接光伏，那么可接入光伏节点的取值范围为2-33；容量范围为0-2MW，步长为0.1MW

📚2 运行结果

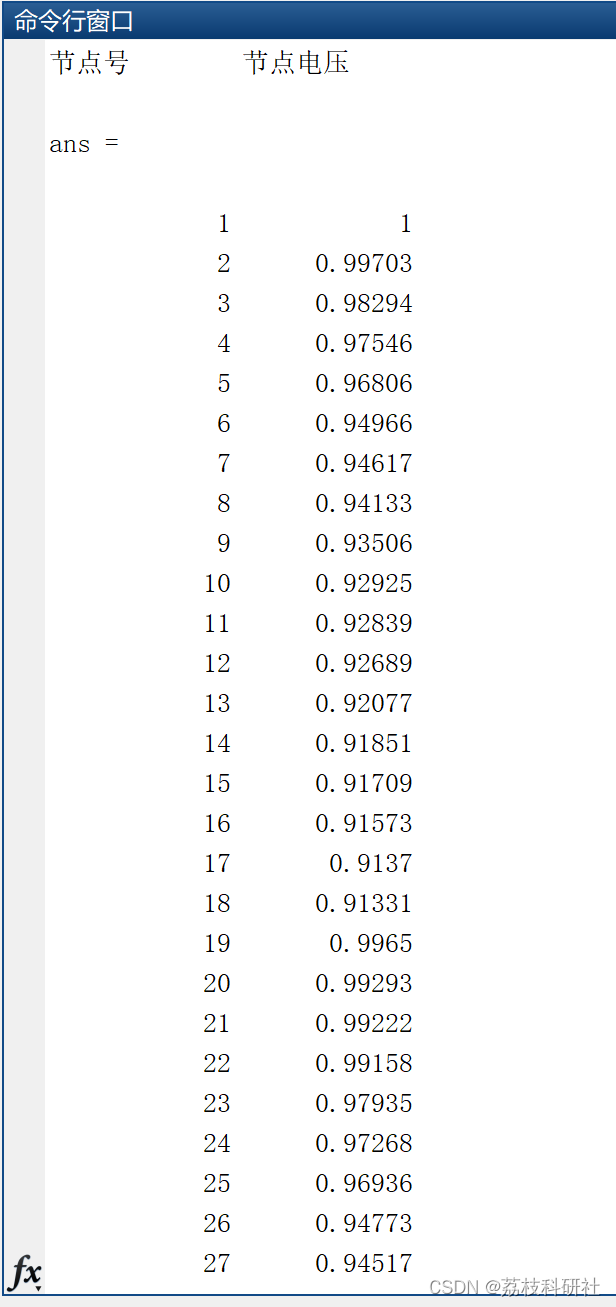
部分代码：

Ppv=sum(x(6:10))*0.1;%光伏消纳总量
f1=P1*SB;%总损耗
f2=sum(abs(U-1));%电压偏差
w1=100;w2=100;w3=1;
Ec=Ppv-f1;
f3=Ppv/Ec;
F=w1*f1+w2*f2+w3*f3+KU*SU+KI*SI;
disp('网损/kW')
f1*1000
disp('电压偏差/pu：')
f2
disp('出力消纳比为：')
f3

....

xlabel('迭代次数');
ylabel('目标函数值');
title('迭代收敛图')
hold on;
grid on;
disp('光伏接入点为:')
BestSol1.Position(1:5)
disp('对应接入容量为/MW:')
BestSol1.Position(6:10)*0.1