x.1 咖啡机的例子
我们以煮咖啡为例子来做一个判断煮的咖啡是否符合自己预期的实验。假设煮咖啡的好坏有两个因素决定,温度和煮的时间,图中x表示煮的咖啡很好,o表示煮的咖啡不好,我们根据这个实验来建模,并将模型通过TF进行表达如下,
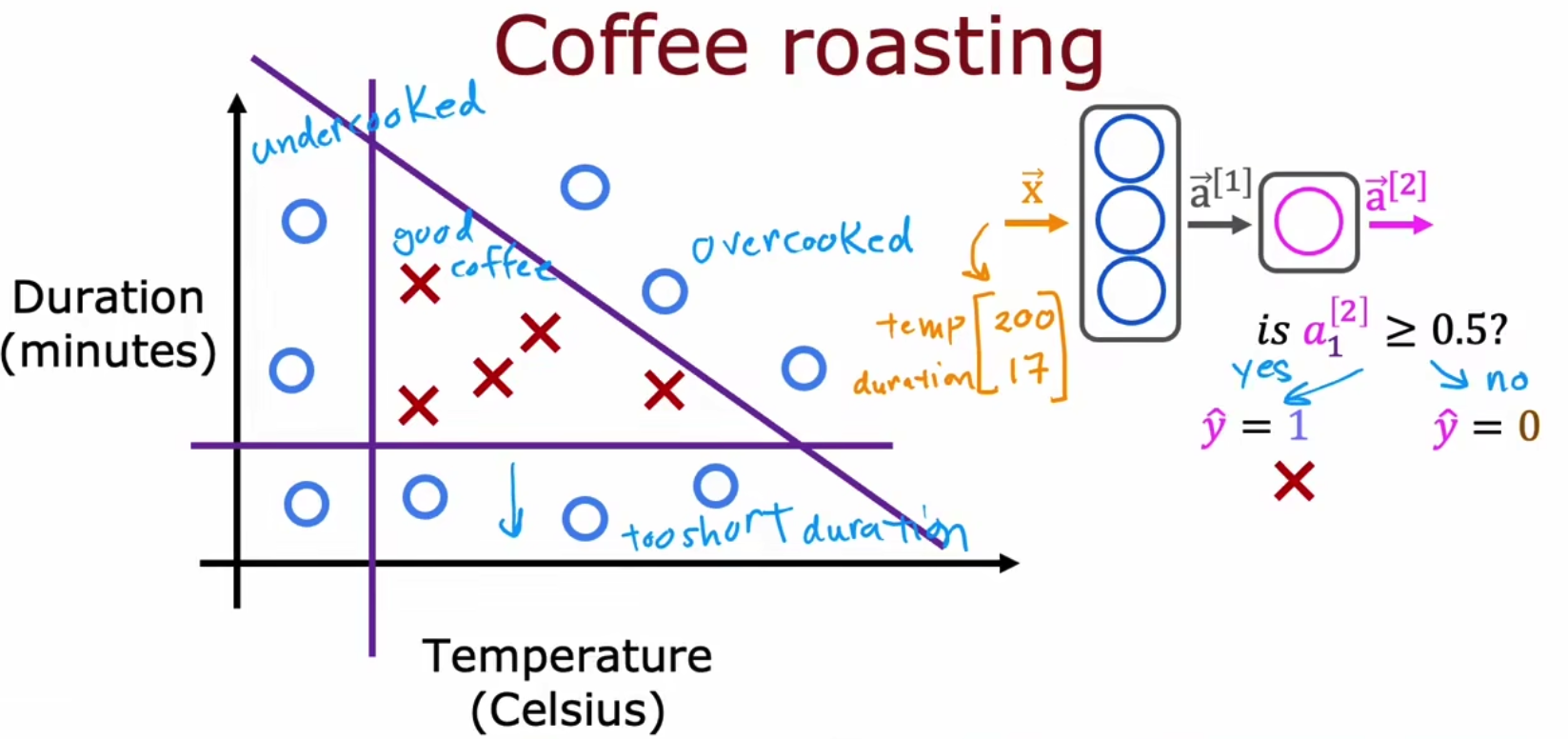
x.2 手写数字识别的分类

x.3 TF数据存储形式
Wu负责了Google团队的TF开发,他和Numpy的数据存储是有些许差异的。我们注意到,例如输入x是一个一维向量,我们将一维向量输入到网络中,但是在TF中,它往往是以一维矩阵输入到网络中,他是[[200, 17]]而不是[200, 17]。

你可能会觉得奇怪,为什么是输入二维矩阵,而不是一维向量,这是因为TF旨在处理大量数学矩阵运算,而非简单的一维向量,是为了数据的统一。



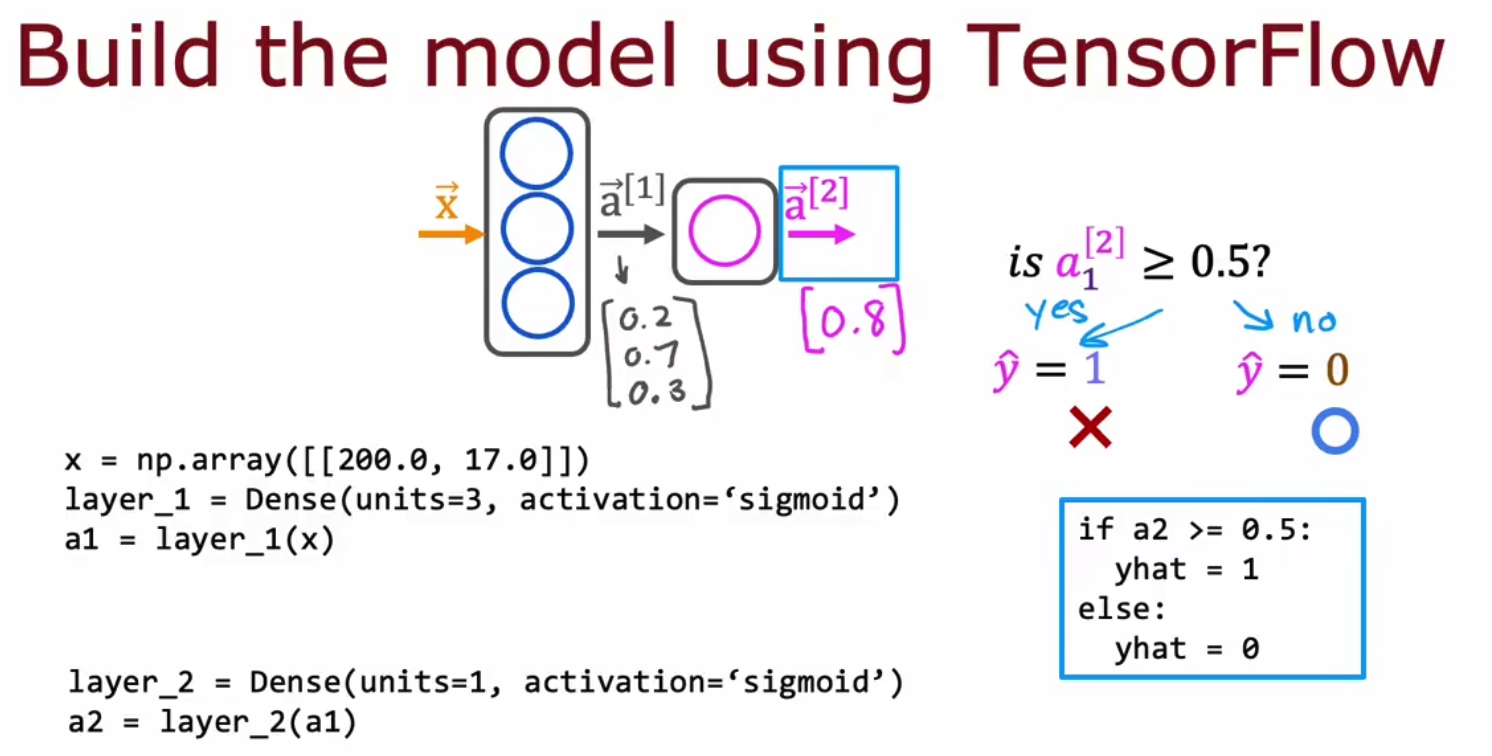
x.4 用TF搭建一个神经网络
我们在原先搭建的网络长如下,


x.5 用numpy来实现神经网络
对于使用numpy实现神经网络,我们使用内置的dot和sigmoid函数便可以很好地实现,下面是神经网络的手动实现,

但是为了方便计算,我们尝试将权重的向量格式改写为矩阵形式,但是我们在每一次乘法运算中仍然取出矩阵的某一列向量,和输入的向量进行乘法,实现如下,我们使用了一个1x2的输入向量,2x3的权重矩阵和1x3的偏置矩阵,最终输出1x3的输出特征矩阵。

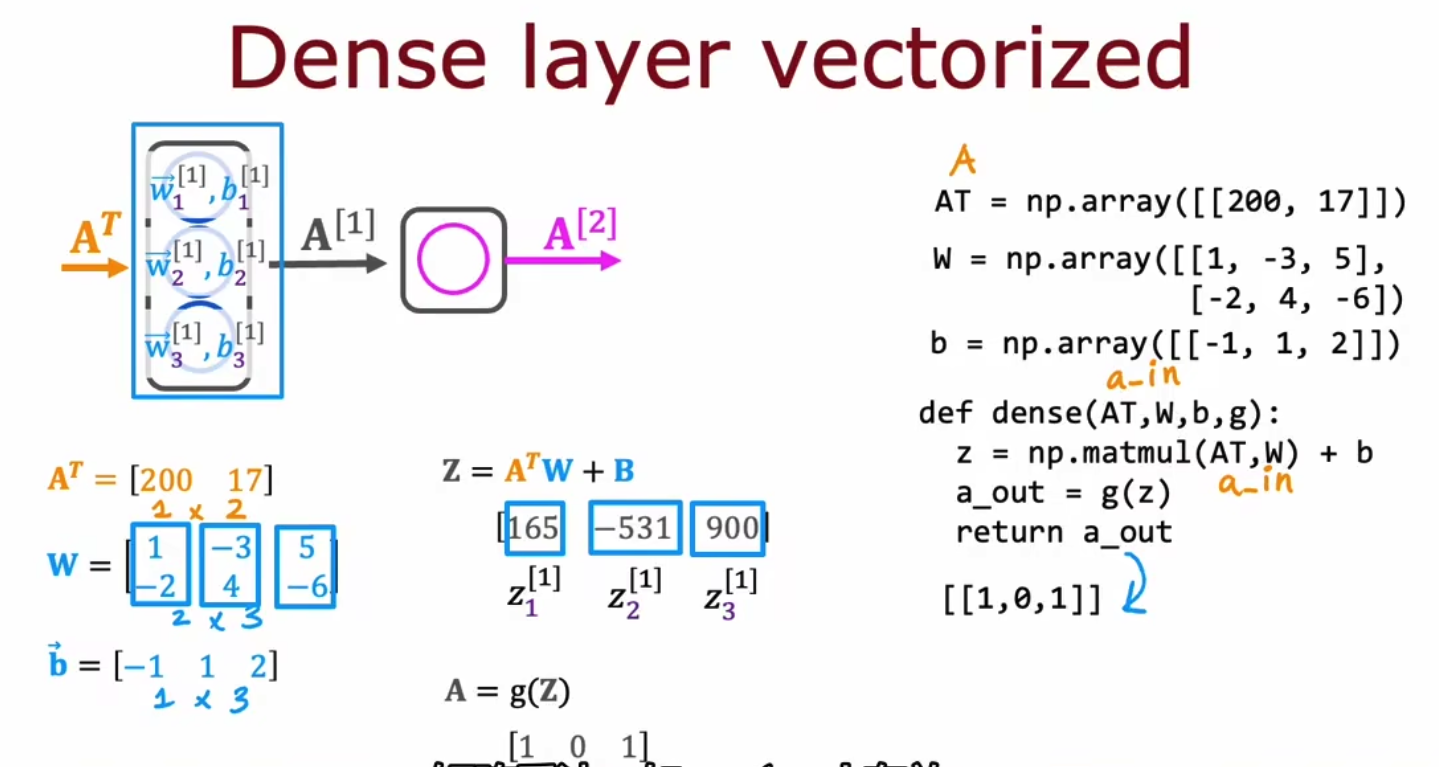
这样的运算虽然变得高效了,但也并不是那么高效,我们为了高效运算往往需要使用Vectorization矢量化后再运算,如下,右侧便是矢量化后运算结果,我们能够发现,所有的向量都变成了矩阵(即至少是2维及以上),使用矩阵乘法matmul代替了向量乘法dot。

x.6 Dot和multiple
对于向量点乘,我们通过将其中一个向量转置后再运用向量乘法或者矩阵乘法能够替换实现,如下是向量和向量的点乘使用向量和向量的乘法替代,
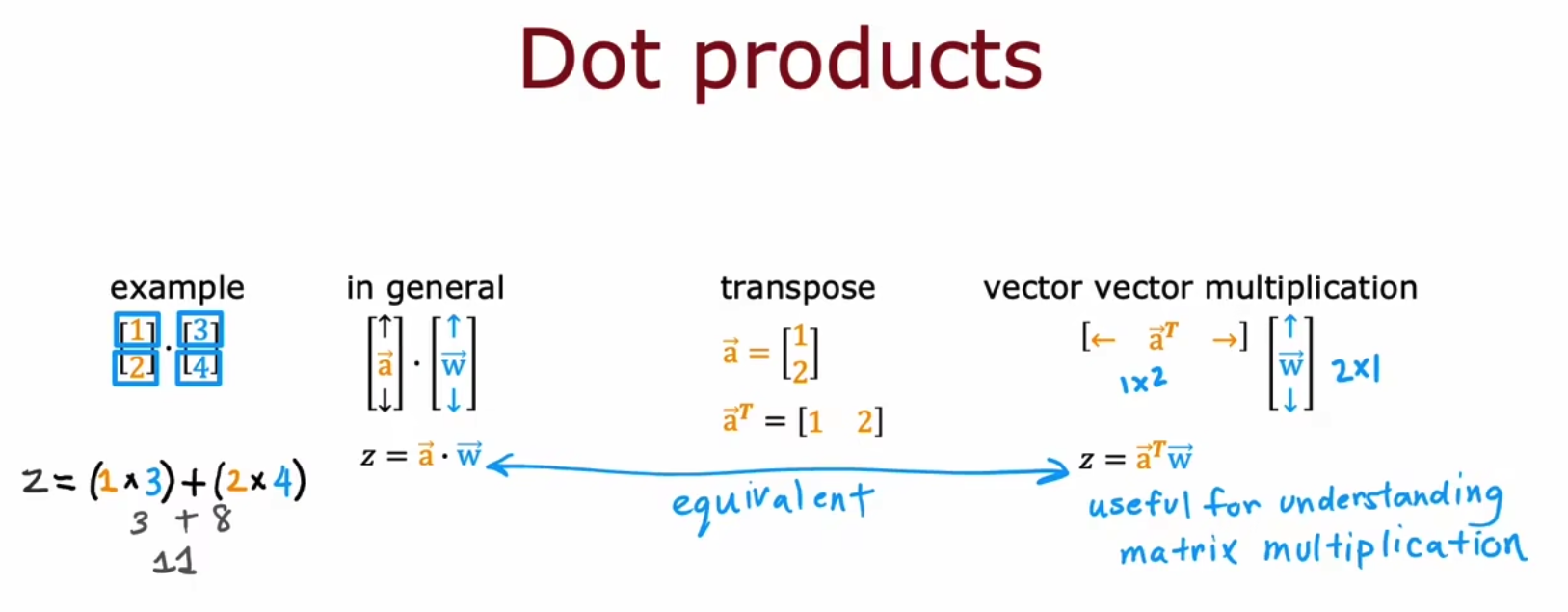
如下是向量以此和矩阵的向量做点乘,使用向量和矩阵的乘法代替,

矩阵中的向量和矩阵中的向量做点积,使用矩阵和矩阵乘法代替,

在Numpy中,矩阵乘法的代码实现,

我们需要注意的是,当我们使用矢量化来加速计算时,我们的输入矩阵是列向量,但是往往需要转置后再进行矩阵乘法。
![[MySql]表的增删查改](https://img-blog.csdnimg.cn/260f16477e8245b991584552c6d6e1c2.png)