1. 问题

  假设有一排房屋，每个房屋里都存放着一定数量的财宝。相邻的房屋装有相互连通的防盗系统，如果两个相邻的房屋在同一晚上被小偷闯入，系统会自动报警。
  求解的问题是，小偷在不触发警报的情况下，一晚上最多能偷到多少财宝。

2. 解题思路（状态转移方程）

2.1 状态转移方程

  状态转移方程是系统动力学中描述系统状态随时间演变的数学方程。这种方程通常用来表示系统的状态如何从一个时间点转移到下一个时间点。在控制理论、物理系统建模、经济学等领域，状态转移方程是非常常见且重要的概念。
  一般而言，状态转移方程可以用如下的形式表示：

  ·x(t)是系统在时间t的状态向量。
  ·u(t)是在时间t的输入向量。
  ·A是状态转移矩阵，描述系统状态如何随时间演变。
  ·B是输入矩阵，描述输入如何影响状态的演变。
  这个方程表示系统在下一个时间点的状态x(t+1)是当前状态x(t)通过矩阵A的变换加上输入u(t)通过矩阵B的变换得到的。
  在一些应用中，状态转移方程也可能包含时间的影响、随机扰动等因素，具体形式可能会更加复杂。

2.2 解题思路

  为了应用状态转移方程解决这个问题，可以将问题抽象成一个动态规划问题，其中状态表示小偷在每个房屋处的状态。假设有n个房屋，用f()表示小偷在第个房屋时能够获得的最大财物价值。状态转移方程可以表示为:

  f(i)是在第个房屋时能够获得的最大财物价值价值[i是第我个房屋中的财物价值。
  f(i-1)表示小偷选择不盗窃当前房屋，所以能够获得的最大财物价值与前一个房屋的最大财物价值相同。
  F(i-2)+value[i]表示小偷选择盗窃当前房屋，所以能够获得的最大财物价值为前两个房屋的最大财物价值加上当前房屋的财物价值。
  这个状态转移方程反映了一个典型的动态规划问题，通过递推求解，可以找到小偷在整个房屋序列中能够获得的最大财物价值。这个问题的动态规划解法避免了重复计算，提高了效率

3. 代码设计思路

  问题表述：给定一个整数数组 nums，表示每个房屋中的财宝数量，小偷在不触发警报的情况下，一晚上最多能偷到多少财宝。
  例如，给定 nums = [1, 2, 3, 1]，表示有四个房屋，分别存放着 1、2、3、1 单位的财宝。如果小偷选择偷窃第1号和第3号房屋，那么最终能偷到的财宝最大，为 1 + 3 = 4。
  这个问题可以用动态规划来解决。设 dp[i] 表示在前 i 个房屋中能偷到的最大财宝数量。对于第 i 个房屋，小偷有两个选择：要么偷这个房屋，要么不偷。如果偷第 i 个房屋，那么最大财宝数量就是前 i-2 个房屋的最大财宝数量加上第 i 个房屋中的财宝数量。如果不偷第 i 个房屋，那么最大财宝数量就是前 i-1 个房屋的最大财宝数量。因此，可以得到状态转移方程：

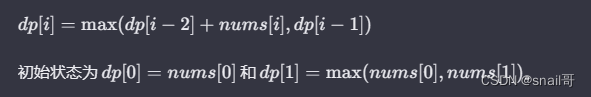
3. 代码实现

def rob(nums):# 如果房屋为空，则返回0if not nums:return 0# 如果只有一个房屋，则抢劫该房屋if len(nums) == 1:return nums[0]# 初始化一个列表，用于保存房屋的最大抢劫金额# dp[i] 表示在前i个房屋中能够抢到的最大金额dp = [0] * len(nums)# 初始化前两个房屋的最大抢劫金额dp[0] = nums[0]dp[1] = max(nums[0], nums[1])# 从第三个房屋开始计算最大抢劫金额for i in range(2, len(nums)):# 动态规划递推公式：dp[i] = max(dp[i-1], dp[i-2] + nums[i])dp[i] = max(dp[i-1], dp[i-2] + nums[i])# 返回最后一个房屋的最大抢劫金额return dp[-1]# 示例
nums = [2, 7, 9, 3, 1]
result = rob(nums)
print(result)