什么是线性回归?
线性回归(Linear regression)是一种利用线性函数对自变量(特征)和因变量之间的关系进行建模的方法。线性回归是机器学习中一种广泛使用的基本回归算法。含有有多个特征的线性回归称为多元线性回归。
假设有 nn 个特征(自变量)x1x1,x2x2,...,xnxn,一个输出变量 yy,线性回归的一般形式表示如下:
y=f(x)=w1x1+w2x2+...+wnxn+b .(1)(1)y=f(x)=w1x1+w2x2+...+wnxn+b .
其中,系数 w1w1,w2w2,...,wnwn 为特征的权重,bb 为偏置。
上式也可以写成向量的形式:y=f(x)=wTx+b .(2)(2)y=f(x)=wTx+b .
其中,x=[x1,x2,...,xn]x=[x1,x2,...,xn],w=[w1,w2,...,wn]w=[w1,w2,...,wn].
看不懂吧,我也看不懂,直接上图,有图有真相。
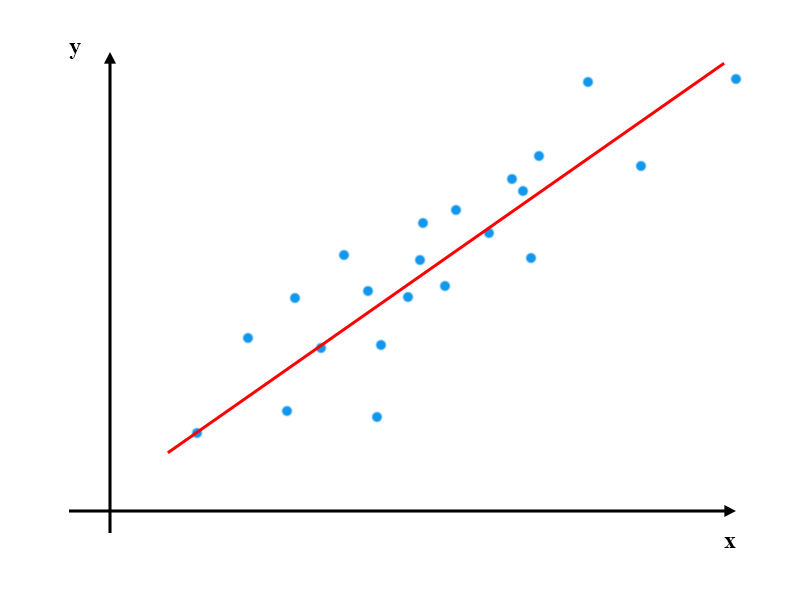
蓝色表示数据点,红色直线表示最终求得的线性回归结果。
几种线性回归算法:
最小二乘法:
• 它通过 最小化误差的平方和 ,寻找数据的最佳函数匹配。
• 利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间 误差的平方 和 为最小。
• 假设我们现在有一系列的数据点(xi,yi) (i=1,…,m),那么由我们给出的拟合函数h(x)得到的估计量就是h(xi)
• 残差:ri = h(xi) – yi
• 三种范数:
1. ∞-范数:残差绝对值的最大值,即所有数据点中残差距离的最大值:
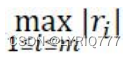
2. 1-范数:绝对残差和,即所有数据点残差距离之和:

3. 2-范数:残差平方和:
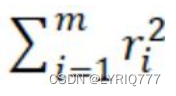
• 拟合程度,用通俗的话来讲,就是我们的拟合函数h(x)与待求解的函数y之间的相似性。那么
2-范数越小,自然相似性就比较高了。
所以式子就可以写为:
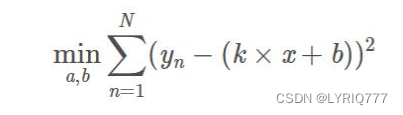
分别对k和b求偏导,然后令偏导数为0,即可获得极值点。
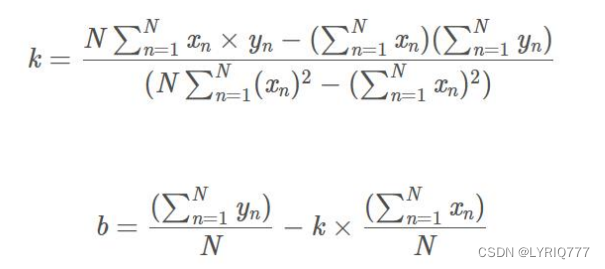
RANSAC:
• 随机采样一致性(random sample consensus)。
• RANSAC是一种思想 ,一个求解已知模型的参数的框架。 它不限定某一特定的问题,可以是计 算机视觉的问题,同样也可以是统计数学,甚至可以是经济学领域的模型参数估计问题。
• 它是一种迭代的方法,用来在一组包含离群的被观测数据中估算出数学模型的参数。 RANSAC是一个非确定性算法,在某种意义上说,它会产生一个在一定概率下合理的结果,其允许使用更多次的迭代来使其概率增加。
• RANSAC的基本假设是 “内群”数据可以通过几组模型参数来叙述其数据分布,而“离群”数据则是不适合模型化的数据。 数据会受噪声影响,噪声指的是离群,例如从极端的噪声或错误解释有关数据的测量或不正确的假设。 RANSAC假定,给定一组(通常很小的)内群,存在一个 程序,这个程序可以估算最佳解释或最适用于这一数据模型的参数。

RANSAC算法的输入:
1. 一组观测数据(往往含有较大的噪声或无效点),
2. 一个用于解释观测数据的参数化模型, 比如 y=ax+b
3. 一些可信的参数。
RANSAC 的步骤:
1. 在数据中随机选择几个点设定为内群
2. 计算适合内群的模型 e.g. y=ax+b ->y=2x+3 y=4x+5
3. 把其它刚才没选到的点带入刚才建立的模型中,计算是否为内群 e.g. hi=2xi+3->ri
4. 记下内群数量
5. 重复以上步骤
6. 比较哪次计算中内群数量最多,内群最多的那次所建的模型就是我们所要求的解
注意 : 不同问题对应的数学模型不同,因此在计算模型参数时方法必定不同,RANSAC的作用不在于
计算模型参数。(这导致ransac的缺点在于要求数学模型已知)
这里有几个问题:
1. 一开始的时候我们要随机选择多少点(n)
2. 以及要重复做多少次(k)
• 假设每个点是真正内群的概率为 w:
w = 内群的数目/(内群数目+外群数目)
• 通常我们不知道 w 是多少, w^n是所选择的n个点都是内群的机率, 1-w^n 是所选择的n个点至少有一个不是内群的机率, (1 − w^n)^k 是表示重复 k 次都没有全部的n个点都是内群的机率, 假设算法跑 k 次以后成功的机率是p,那么,
1 − p = (1 − w^n)^k
p = 1 − (1 − w^n)^k
• 我们可以通过P反算得到抽取次数K,K=log(1-P)/log(1-w^n)。
• 所以如果希望成功机率高:
• 当n不变时,k越大,则p越大; 当w不变时,n越大,所需的k就越大。
• 通常w未知,所以n 选小一点比较好。
RANSAC 的优缺点:
优点:
1. 它能鲁棒的估计模型参数。例如,它能从包含大量局外点的数据集中估计出高精度的参数。
缺点:
1. 它计算参数的迭代次数没有上限;如果设置迭代次数的上限,得到的结果可能不是最优的结果,甚至可能得到错误的结果。
2. RANSAC只有一定的概率得到可信的模型,概率与迭代次数成正比。
3. 它要求设置跟问题相关的阀值。
4. RANSAC只能从特定的数据集中估计出一个模型,如果存在两个(或多个)模型,RANSAC不能找到别的模型。
5. 要求数学模型已知
RANSAC 与最小二乘法
• 生产实践中的数据往往会有一定的偏差。
• 例如我们知道两个变量X与Y之间呈线性关系,Y=aX+b,我们想确定参数a与b的具体值。通过实验,可以得到一组X与Y的测试值。虽然理论上两个未知数的方程只需要两组值即可确认,但由于系统误差的原因,任意取两点算出的a与b的值都不尽相同。我们希望的是,最后计算得出的理论模型与测试值的误差最小。
• 最小二乘法:通过计算最小均方差关于参数a、b的偏导数为零时的值。事实上,很多情况下,最小二乘法都是线性回归的代名词。
• 遗憾的是,最小二乘法只适合于误差较小的情况。
• 在模型确定以及最大迭代次数允许的情况下,RANSAC总是能找到最优解。(对于包含80%误差的数据集,RANSAC的效果远优于直接的最小二乘法。)
• 由于一张图片中像素点数量大,采用最小二乘法运算量大,计算速度慢。

哈希算法:
1. 均值哈希算法aHash
步骤
1. 缩放:图片缩放为8*8,保留结构,除去细节。
2. 灰度化:转换为灰度图。
3. 求平均值:计算灰度图所有像素的平均值。
4. 比较:像素值大于平均值记作1,相反记作0,总共64位。
5. 生成hash:将上述步骤生成的1和0按顺序组合起来既是图片的指纹(hash)。
6. 对比指纹:将两幅图的指纹对比,计算汉明距离,即两个64位的hash值有多少位是不一样的,不相同位数越少,图片越相似。
汉明距离
两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。

2. 差值哈希算法dHash
差值哈希算法相较于均值哈希算法,前期和后期基本相同,只有中间比较hash有变化。
步骤
1. 缩放:图片缩放为 8*9 ,保留结构,除去细节。
2. 灰度化:转换为灰度图。
3. 求平均值:计算灰度图所有像素的平均值。 ---这步没有,只是为了与均值哈希做对比
4. 比较:像素值大于后一个像素值记作1,相反记作0。本行不与下一行对比,每行9个像素,
八个差值,有8行,总共64位
5. 生成hash:将上述步骤生成的1和0按顺序组合起来既是图片的指纹(hash)。
6. 对比指纹:将两幅图的指纹对比,计算汉明距离,即两个64位的hash值有多少位是不一样的,不相同位数越少,图片越相似。
3. 感知哈希算法pHash
均值哈希算法过于严格,不够精确,更适合搜索缩略图,为了获得更精确的结果可以选择感知哈希
算法,它采用的是DCT(离散余弦变换)来降低频率的方法。
步骤:
1. 缩小图片:32 * 32是一个较好的大小,这样方便DCT计算
2. 转化为灰度图:把缩放后的图片转化为灰度图。
3. 计算DCT:DCT把图片分离成分率的集合
4. 缩小DCT:DCT计算后的矩阵是32 * 32,保留左上角的8 * 8,这些代表图片的最低频率。
5. 计算平均值:计算缩小DCT后的所有像素点的平均值。
6. 进一步减小DCT:大于平均值记录为1,反之记录为0.
7. 得到信息指纹:组合64个信息位,顺序随意保持一致性。
8. 最后比对两张图片的指纹,获得汉明距离即可。
离散余弦变换 DCT




![[工业互联-16]:工业Windows操作系统与实时性方案](https://img-blog.csdnimg.cn/1442be6493584156a910007219a543c6.png)