先来一个模棱两可的说法:因为精度丢失、存储溢出的问题
先复习一下二进制的转换方法:
- 整数:除以基数,取余,自底向上
- 小数:乘以基数,取整,自顶向下

接着,复习一下双精度浮点数(double)
- Number 类型使用IEEE754 标准 64位 存储
- 符号位:1位,0 表示正数,1 表示负数
- 指数位:11位,固定值(1023)+ 指数实际值
- (2 ^ (e-1)) - 1 => (2 ^ (11 - 1)) - 1 = 1023
- 这一步看不懂,可先跳过,待会解释
- 小数位:52位
- 双精度浮点数即为每个数值分配 64位存储空间,以科学计数法的方式存储
中间插播一个小内容:怎么理解指数位
1、IEEE 754 标准中的双精度浮点数采用了带有偏移量的指数表示
2、具体来说,双精度浮点数的指数部分是一个11位的二进制数,其中最小值是全0(00000000000),最大值是全1(11111111111)。这11位的二进制数会被解释为一个无符号整数,然后从中减去一个偏移值来得到最终的指数。
3、IEEE 754 双精度浮点数的指数偏移值是 2 ( k − 1 ) − 1 2^{(k-1)} - 1 2(k−1)−1,其中 k 是指数部分的位数。对于双精度浮点数,k 是11,所以偏移值是 2 ( 11 − 1 ) − 1 = 1023 2^{(11-1)} - 1 = 1023 2(11−1)−1=1023。
4、例如,如果指数部分的二进制表示是 01111111111,那么对应的无符号整数是 2 10 − 1 = 1023 2^{10} - 1 = 1023 210−1=1023。然后,减去偏移值 1023,最终得到实际的指数值为0。
5、这个偏移量的使用允许浮点数表示非常大和非常小的数,因为指数的范围可以从负数到正数。同时,由于使用偏移值,指数部分的二进制表示中并不包含真实的指数值,而是需要通过减去偏移值来得到真实的指数。
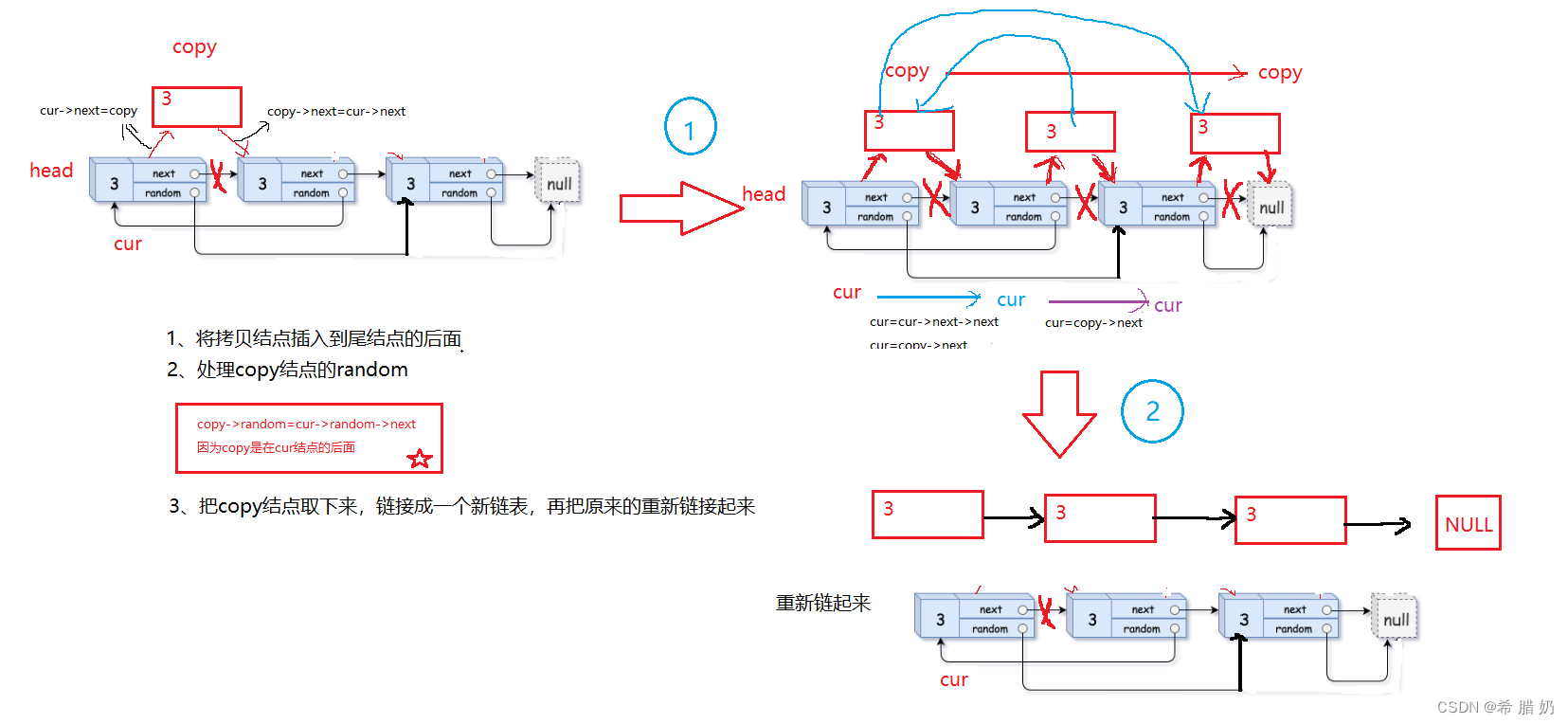
了解上面两个知识点之后,开始进入正文
第一步:0.1 转换二进制为:0.00011001…1001(循环)
第二步:二进制转换为科学计数法 = 1.1001 * 2^ (-4)
第三步:计算指数位 1023 + (-4) = 1019 = 01111111011
第四步:计算小数位,为1001无限循环
因此,0.1 = 符号位0 + 指数位01111111011 + 小数位1001…
由于小数位只有52为,因此第53位为1,截取保存的时候进了1,所以发生了精度丢失。 即后四位小数为 1001 + 1 = 1010
针对于0.2也进行同样分析,相加的时候同样也出现了截取保存的情况,即出现第二次精度丢失,所以最终转换为10进制的时候为 0.30000000000000004
综上所述:
1、由于js采用二进制处理数据,用IEEE 754双精度浮点数标准来存储 Number 类型
2、精度丢失非JS问题,而是IEEE 754标准存储位有限
3、过程中出现了两次精度丢失问题,一次在存储,一次在相加
解决方案:
1、两个数分别乘以100,得到结果再除以100

![13.求面积[有问题]](https://img-blog.csdnimg.cn/8761d080cb1e4fc1aac3be9ff8ae27c3.png)