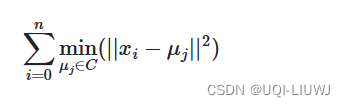1 K-means介绍
1.0 方法介绍
- KMeans算法通过尝试将样本分成n个方差相等的组来聚类,该算法要求指定群集的数量。它适用于大量样本,并已在许多不同领域的广泛应用领域中使用。
- KMeans算法将一组样本分成不相交的簇,每个簇由簇中样本的平均值描述。这些平均值通常称为簇的“质心”;
- 注意,质心通常不是样本点,尽管它们存在于相同的空间中。
- KMeans算法旨在选择最小化惯性或称为群内平方和标准的质心:
1.1 惯性的缺点
- 惯性可以被认为是衡量簇内部一致性的一种度量。它有各种缺点:
- 惯性假设簇是凸形的和各向同性的,但这不总是情况。
- 它对于拉长的簇或形状不规则的流形反应不佳。
- 惯性不是一个规范化的度量:
- 我们只知道较低的值更好,零是最优的。但是在非常高维的空间中,欧几里得距离往往会变得膨胀(这是所谓的“维数诅咒”的一个实例)。
- ——>在k均值聚类之前运行一个降维算法,如主成分分析(PCA),可以缓解这个问题并加快计算速度。
- 惯性假设簇是凸形的和各向同性的,但这不总是情况。
- 以下是几个K-means效果不加的例子:

- clusters的数量不是最优
- 各向异性的cluster分布
- 方差不同
- 各个簇数量不同
1.2 Kmeans算法的步骤
- K均值算法通常被称为劳埃德算法(Lloyd's algorithm)。简单来说,该算法有三个步骤
- 第一步选择初始质心,最基本的方法是从数据集中选择样本
- 初始化之后,K均值算法由两个步骤的循环组成
- 第一个步骤是将每个样本分配给最近的质心
- 第二步是通过取分配给每个前一个质心的所有样本的平均值来创建新的质心
- 计算旧质心和新质心之间的差异,并重复这最后两个步骤,直到这个值小于一个阈值(直到质心不再有显著移动为止)
- K均值算法等同于期望最大化算法,带有一个小的、全相等的、对角线协方差矩阵

- 给定足够的时间,K均值总会收敛,但这可能是到一个局部最小值
- 这在很大程度上取决于质心的初始化
- 因此,计算通常会进行多次,质心的初始化也各不相同
- 一个帮助解决这个问题的方法是k-means++初始化方案(init='k-means++')
- 这样初始化质心通常会相互远离,导致比随机初始化更好的结果
2 sklearn.cluster.KMeans
sklearn.cluster.KMeans(n_clusters=8, *, init='k-means++', n_init='warn', max_iter=300, tol=0.0001, verbose=0, random_state=None, copy_x=True, algorithm='lloyd')2.1 主要参数
| n_clusters | 簇的数量 |
| init |
|
| n_init |
|
| max_iter |
|
| tol | 两次连续迭代的簇中心的Frobenius范数差异来声明收敛的相对容忍度 |
2.2 举例
from sklearn.cluster import KMeans
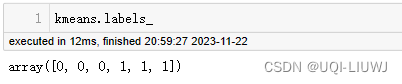
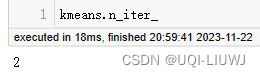
import numpy as npX = np.array([[1, 2], [1, 4], [1, 0],[10, 2], [10, 4], [10, 0]])kmeans=KMeans(n_clusters=2,n_init='auto').fit(X)2.2.1 属性
| cluster_centers_ | 簇中心的坐标
|
| labels_ | 每个点的标签
|
| inertia_ | 样本到最近簇中心的平方距离之和,如果提供了样本权重,则按样本权重加权
|
| n_iter_ | 运行的迭代次数
|
2.2.2 fit
fit(X, sample_weight=None)sample_weight 是X中每个观测的权重。如果为None,则所有观测都被赋予相等的权重
3 sklearn.cluster.kmeans_plusplus
类似于使用k_means++来进行
sklearn.cluster.kmeans_plusplus(X, n_clusters, *, sample_weight=None, x_squared_norms=None, random_state=None, n_local_trials=None)| X | 用来选择初始种子的数据 (也就是KMeans里面fit的内容) |
| n_cluster | 要初始化的质心数量 |
| sample_weight | X中每个观测的权重 |
3.1 返回值:
centers:形状为(n_clusters, n_features) ,k-means的初始中心。
indices:形状为(n_clusters,) 在数据数组X中选择的中心的索引位置。对于给定的索引和中心,X[index] = center
3.2 举例
from sklearn.cluster import kmeans_plusplus
import numpy as npX = np.array([[1, 2], [1, 4], [1, 0],[10, 2], [10, 4], [10, 0]])kmeans_plusplus(X,n_clusters=2)
'''
(array([[10, 0],[ 1, 4]]),array([5, 1]))
'''4 Mini Batch K-Means
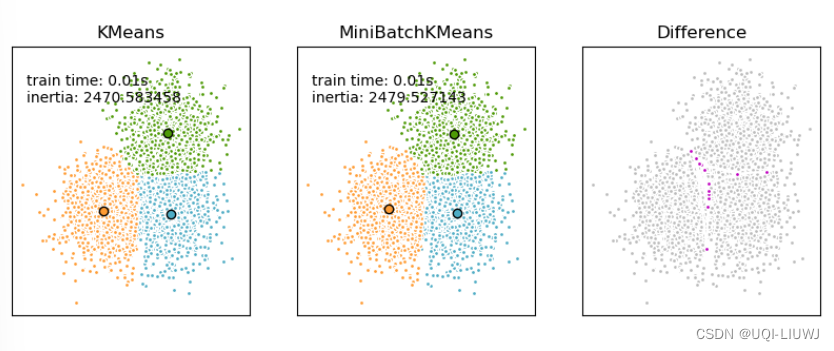
- MiniBatchKMeans是KMeans算法的一个变种,它使用小批量(mini-batches)来减少计算时间,同时仍然试图优化相同的目标函数
- 小批量是输入数据的子集,在每次训练迭代中随机采样
- 这些小批量大大减少了收敛到局部解所需的计算量
- 与其他减少k-means收敛时间的算法不同,mini-batch k-means产生的结果通常只比标准算法稍差
- 该算法在两个主要步骤之间迭代,类似于传统的k-means算法
- 在第一步中,从数据集中随机抽取样本,形成一个小批量.然后,这些样本被分配到最近的质心
- 在第二步中,更新质心。与k-means不同,这是按样本进行的
- 对于小批量中的每个样本,通过取样本及其之前分配到该质心的所有样本的流式平均值来更新分配的质心。
- 这样做的效果是随着时间的推移减少质心变化的速率。
- 这些步骤执行直到收敛或达到预定的迭代次数为止
- MiniBatchKMeans比KMeans收敛得更快,但结果的质量有所降低
4.1 sklearn.cluster.MiniBatchKMeans
class sklearn.cluster.MiniBatchKMeans(n_clusters=8, *, init='k-means++', max_iter=100, batch_size=1024, verbose=0, compute_labels=True, random_state=None, tol=0.0, max_no_improvement=10, init_size=None, n_init='warn', reassignment_ratio=0.01)4.1.1 主要参数
| n_clusters | 簇的数量 |
| init |
|
| max_iter |
|
| batch_size | mini batch的大小,默认是1024 |
| n_init |
|
4.1.2 属性
还是那些:cluster_centers,labels_,inertia_,n_iter_,n_steps
4.1.3 方法
方法上fit,tranform,predict这些都有,多了一个partial_fit,表示使用一个mini-batch的样本
4.2 举例
from sklearn.cluster import MiniBatchKMeans
import numpy as npX = np.array([[1, 2], [1, 4], [1, 0],[10, 2], [10, 4], [10, 0]])mini_kmeans=MiniBatchKMeans(n_clusters=2).fit(X)mini_kmeans.cluster_centers_
'''
array([[ 1. , 2.57142857],[10. , 2. ]])
'''mini_kmeans.labels_
#array([0, 0, 0, 1, 1, 1])