题意：略，题中较清晰。

用二叉查找树来存储数据，为了增加效率，尽量使左子树和右子树的深度差不超过一，这样可以时间控制在logn，效率比较高。

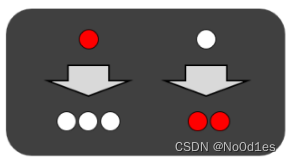
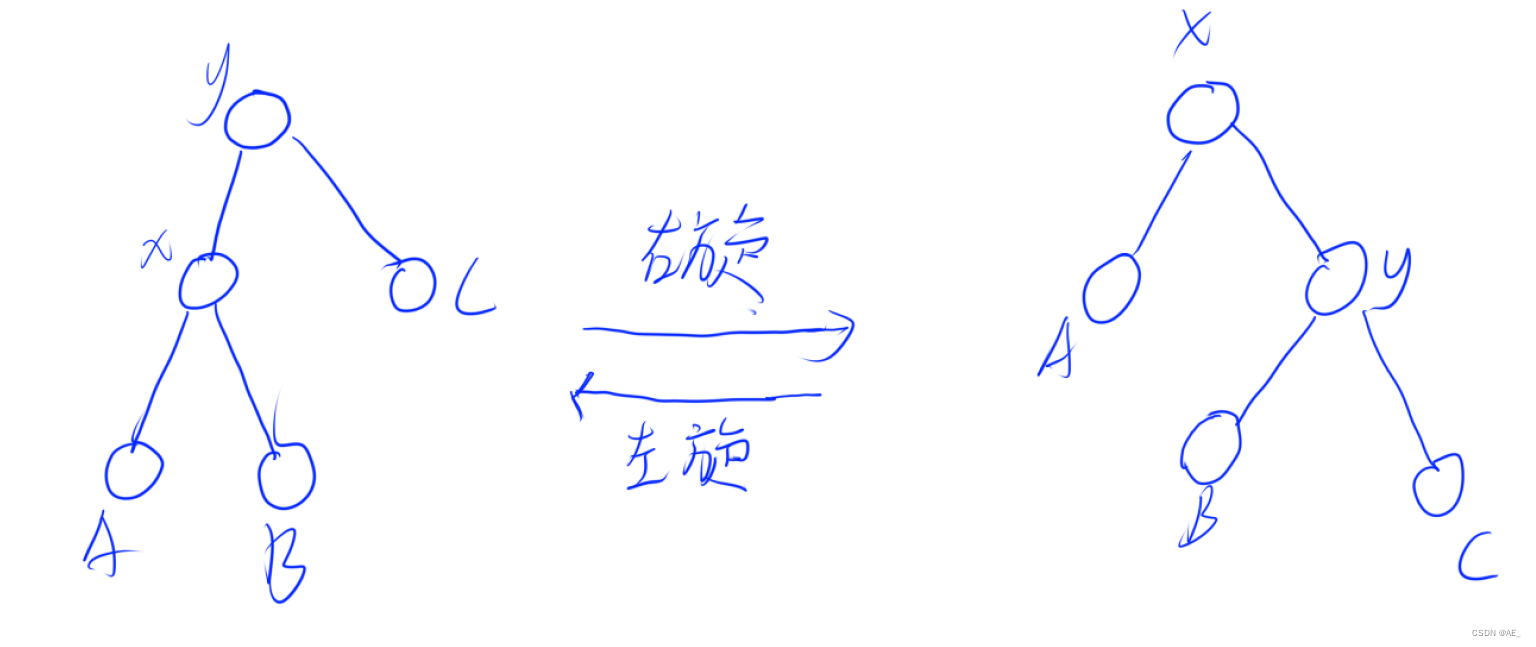
右旋和左旋，目的是为了维护二叉树的操作，使其尽量平衡。

int n, m;
int o[N];
struct Node { // 节点int l, r; // 左儿子，右儿子int key, val; // 数据值，随机值（用以维护二叉树尽量平衡的条件） int cnt, size; // 当前key值的数量，当前子树的所有节点的cnt值和
} tr[N];
int root, idx; // 根节点，下一个可以分配的节点序号void push_up(int p) { // 与线段树操作的意义一样tr[p].size = tr[tr[p].l].size + tr[tr[p].r].size + tr[p].cnt; // 左右子树的size和加上本身cnt
}int get_node(int key) { // 创建一个节点，返回节点序号tr[++ idx].key = key; // 初始化keytr[idx].val = rand(); // 随机一个01给valtr[idx].cnt = tr[idx].size = 1; // 数量为1，只有本身return idx; // 返回序号
}void build() { // 建立一个空的二叉树，只有两个哨兵，无穷大与无穷小get_node(-INF), get_node(INF);root = 1, tr[1].r = 2; push_up(root);
}void zig(int &p) { // 右旋int q = tr[p].l; // q为根节点左儿子tr[p].l = tr[q].r, tr[q].r = p, p = q; // 对应图片分析push_up(tr[p].r), push_up(p); // 更新size值
}void zag(int &p) { // 左旋int q = tr[p].r; // q为根节点右儿子tr[p].r = tr[q].l, tr[q].l = p, p = q; // 对应图片分析push_up(tr[p].l), push_up(p); // 更新size值
}void insert(int &p, int key) { // 插入一个节点keyif(!p) p = get_node(key); // 该key值未出现过，创建一个新的节点，并将序号返回到上一级else if(tr[p].key == key) tr[p].cnt ++; // 出现过，直接cnt数量加一else if(tr[p].key > key) { // 应该插在左儿子insert(tr[p].l, key); // 递归左儿子if(tr[tr[p].l].val > tr[p].val) zig(p); // 左儿子val值大于本身，右旋处理} else { // 应该插在右儿子insert(tr[p].r, key); // 递归右儿子if(tr[tr[p].r].val > tr[p].val) zag(p); // 右儿子var值大于本身，左旋处理}push_up(p); // 更新size状态return ;
}void remove(int &p, int key) { // 删除一个key值节点if(!p) return ; // 没找到，直接结束if(tr[p].key == key) { // 找到key值节点if(tr[p].cnt > 1) tr[p].cnt --; // 数量不唯一，直接减一即可else if(tr[p].l || tr[p].r) { // 数量唯一且存在儿子if(!tr[p].r || tr[tr[p].l].val > tr[tr[p].r].val) {// 右儿子存在或者左儿子var值大于右儿子，右旋处理zig(p);remove(tr[p].r, key);// 右旋之后key值节点交换到当前p节点的右儿子，遍历右儿子，一直递归直到没有儿子的时候删除} else {// 应该进行左旋处理zag(p);remove(tr[p].l, key);// 左旋之后key值节点交换到当前p节点的左儿子，遍历左儿子，一直递归直到没有儿子的时候删除}} else p = 0; // 数量唯一且没有儿子，直接删除即可。} else if(tr[p].key > key) remove(tr[p].l, key); // key值点在左儿子else remove(tr[p].r, key); // key值点在右儿子push_up(p);
}int get_rank_by_key(int p, int key) { // 根据key值找排名if(!p) return 1;  // 没找到直接return 1，因为洛谷这个题说的是不存在的数的排名为比它的数量加一if(tr[p].key == key) return tr[tr[p].l].size + 1; // 找到key值，返回key值在当前子树的排名if(tr[p].key > key) return get_rank_by_key(tr[p].l, key);// key在左子树return get_rank_by_key(tr[p].r, key) + tr[tr[p].l].size + tr[p].cnt; // key在右子树，因为左子树以及本身都是比它小的，所以需要加上这些数量，再去递归右子树，计算key值在右子树的排名
}
int get_key_by_rank(int p, int rank) {  // 找到排名为rank的key值if(!p) return INF; // 没找到，不存在这个排名的数if(tr[tr[p].l].size >= rank) return get_key_by_rank(tr[p].l, rank); // 在左子树if(tr[tr[p].l].size + tr[p].cnt >= rank) return tr[p].key; // 在本身return get_key_by_rank(tr[p].r, rank - tr[tr[p].l].size - tr[p].cnt); // 在右子树，需要减去左子树以及本身的数量	
}
int get_prev(int p, int key) { // 获得比key小的最大数if(!p) return -INF; // 没找到if(tr[p].key >= key) return get_prev(tr[p].l, key); // 在左子树return max(tr[p].key, get_prev(tr[p].r, key)); // 本身和右子树都比key小，都有可能，递归右子树与本身进行判断。
}
int get_next(int p, int key) { // 获得比key大的最小数if(!p) return INF; // 没找到if(tr[p].key <= key) return get_next(tr[p].r, key); // 在右子树return min(tr[p].key, get_next(tr[p].l, key));  // 本身和左子树都比key大，都有可能，递归左子树与本身进行判断。
}
inline void sovle() {build();
//	cout << idx << endl;cin >> n;while(n --) {int opt, x;cin >> opt >> x;if(opt == 1) insert(root, x);else if(opt == 2) remove(root, x);else if(opt == 3) cout << get_rank_by_key(root, x) - 1 << endl;else if(opt == 4) cout << get_key_by_rank(root, x + 1) << endl;else if(opt == 5) cout << get_prev(root, x) << endl;else cout << get_next(root, x) << endl;}
}