机器学习（13）--支持向量机-编程知识

一、支持向量机概述

二、Sklearn中的SVM概述

三、线性SVM损失函数

四、sklearn中进行可视化

1、导入模块

2、实例化数据集，可视化

3、网格点制作

4、建立模型并绘制决策边界和超平面

5、常用接口

6、如果数据是环形呢？

五、核函数

1、概述

2、在不同类型数据集下使用不同核函数，进行可视化

3、核函数调参

4、惩罚项系数C

一、支持向量机概述

支持向量机（SVM）是按监督学习方式对数据进行二元分类的广义线性分类器，其决策边界是对学习样本求解的最大边距超平面，可以将问题转换为一个求解凸二次规划的问题。

在线性可分情况下，要在原空间中寻找两类样本最优分类超平面，选出决策边界。在线性不可分情况下，需要加入松弛变量，通过使用非线性映射规则将空间样本升维到高维度空间，来变为线性可分，这样就可以在特征空间中寻找最优分类超平面。

SVM在各种实际问题上都表现优秀，在手写体识别和人脸识别应用广泛，在文本和超文本分类上，因为可以大量减少标准归纳和转换设置中对标记训练实例的需求，也是举足轻重的存在。另外，SVM也被用在图像分类，图像分割系统，在生物学和其他科学上SVM也备受青睐。

支持向量机的不同功能

	功能
监督学习	线性二分类与多分类（Linear Support Vector Classfication）非线性二分类与多分类（Support Vector Classfication，SVC）普通连续型变量的回归（SVR）概率型连续变量的回归（Bayesian SVM）
无监督学习	支持向量聚类（Support Vector Clustering）异常值检测（One-class SVM）
半监督学习	转导支持向量机（Transductive Support Vector Machines，TSVM）

支持向量机如何工作？

支持向量机通过在一组分布中找出一个超平面作为决策边界，使模型在数据上的分类误差尽量小，尤其是在未知的数据集上的分类误差（泛化误差）尽量小。

决策边界向两个簇平移，直到碰到距离这个决策边界最近的点时停下，形成两个新的超平面，即图中的两条虚线，而虚线间的距离，即蓝色箭头的距离，则为决策边界的边际d。

边际自然是越大越好，如果说边际小，在训练集上可能score很高，但是在测试集上可能出现个别点分类错误的现象，即过拟合现象。

二、Sklearn中的SVM概述

在sklearn中的SVM也有类和函数两种表示方法。线性类LinearSVC和LinearSVC只能支持线性，而其他的类都是可以支持线性和非线性的。

类	含义
svm.LinearSVC	线性支持向量分类
svm.LinearSVR	线性支持向量回归
svm.SVC	非线性支持向量分类
svm.SVR	非线性支持向量回归
svm.NuSVC	Nu支持向量分类
svm.NuSVR	Nu支持向量回归
svm.OneClassSVM	无监督异常值检测
svm.l1_min_c	返回参数C的最低边际

函数	含义
svm.libsvm.cross_validation	SVM专用的交叉验证
svm.libsvm.decision_function	SVM专用的预测边际函数
svm.libsvm.fit	使用libsvm训练模型
svm.libsvm.predict	给定模型预测X的目标值
svm.libsvm.predict_proba	预测概率

三、线性SVM损失函数

问题的关键：就是扩大边际d。

w是参数，垂直与决策边界，x是特征向量，与数据集有关，b是截距。

为什么这三条线的右侧是1,0，-1？

由于w和b都是参数，所以为了使式子更加简洁，两侧同时除以常数，参数只是做了一个变换。新w和新b仍然可以做为变量。

通过一定的数学推导可以求出来，边际 $d=\frac{2}{||w||}$ ，而边际越大越好，所以有了损失函数 $f(w)=\frac{||w||^2}{2}$ 越小越好，如果不加平方，取模运算会导致计算量变大，所以增加了平方的运算。

损失函数计算公式：

$\underset{w,b}{min}\frac{||w||^2}{2}$

$subject \ to \ y_i(\mathbf{w}\cdot \mathbf{x_i}+b)\geqslant 1,i=1,2,\cdots N.$

约束条件形式：（ $\alpha_i$ 是拉格朗日乘数）

拉格朗日乘数的求解需要转化为对偶问题，这一部分过难，先不写了，晕。

决策函数：

其中 $x_{test}$ 作为测试样本，sign函数其实就是sgn函数，括号内大于0时返回1，小于0时返回-1。

四、sklearn中进行可视化

1、导入模块

from sklearn.datasets import make_blobs   #生成聚类数据集
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import numpy as np

2、实例化数据集，可视化

x,y=make_blobs(n_samples=100,centers=2,random_state=0,cluster_std=0.6)
plt.scatter(x[:,0],x[:,1],c=y,s=50,cmap='rainbow')
plt.show()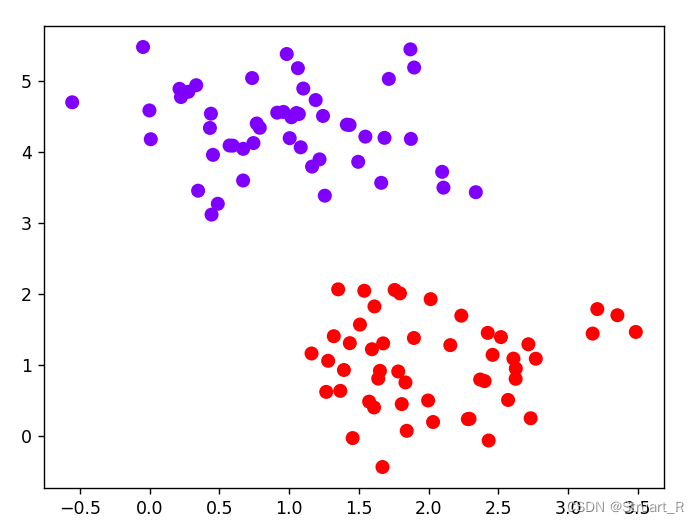

3、网格点制作

制作若干个连续的固定的网格点，为了方便后续决策边界的计算和可视化。

xlim=ax.get_xlim()    #返回上面图的x轴的最小值和最大值
ylim=ax.get_ylim()    #返回上面图的y轴的最小值和最大值#print(xlim,ylim)    #(-0.7425578984849813, 3.3721920271976598) (-0.41872382476349596, 5.754870487889891)axisx=np.linspace(xlim[0],xlim[1],30)          #根据xlim和ylim绘制网格点
axisy=np.linspace(ylim[0],ylim[1],30)
print(axisx,axisy)axisx,axisy=np.meshgrid(axisx,axisy)           #将axisx和axisy分别向y轴和x轴进行扩充（广播）xy=np.vstack([axisx.ravel(),axisy.ravel()]).T  #扩充为30*30的坐标点,后面基于这900个点绘制决策边界plt.scatter(xy[:,0],xy[:,1],s=1,cmap="rainbow")
plt.show()

4、建立模型并绘制决策边界和超平面

clf=SVC(kernel='linear').fit(x,y)                #建模
z=clf.decision_function(xy).reshape(axisx.shape) #每个样本所对应的到决策边界的距离ax=plt.gca()                                     #如果不写将不会生成决策边界
ax.contour(axisx,axisy,z,colors='k',levels=[-1,0,1],                      #代表两个过支持向量的超平面和决策边界alpha=0.5, linestyles=['--','-','--'])           #超平面使用虚线--，决策边界使用实线-ax.set_xlim(xlim)
ax.set_ylim(ylim)plt.scatter(x[:,0],x[:,1],c=y,s=50,cmap='rainbow') 
plt.show()

可以对制作网格点和绘制决策边界和超平面做一个封装函数。

def plot_svc_decision_funtion(model,ax=None):if ax is None:ax=plt.gca()xlim = ax.get_xlim()ylim = ax.get_ylim()x=np.linspace(xlim[0],xlim[1],30)y=np.linspace(ylim[0],ylim[1],30)y,x=np.meshgrid(y,x)xy=np.vstack([x.ravel(),y.ravel()]).TP = model.decision_function(xy).reshape(x.shape)ax.contour(x,y,P,colors='k',levels=[-1,0,1],alpha=0.5,linestyles=['--','-','--'])ax.set_xlim(xlim)ax.set_ylim(ylim)plt.show()

当建模，并绘图时只需要使用如下的代码：

plt.scatter(x[:,0],x[:,1],c=y,s=50,cmap='rainbow')
plot_svc_decision_funtion(clf)

绘制效果：

5、常用接口

clf.predict(x)               #返回预测的label
clf.score(x,y)               #评分（建模时要分训练集和测试集，要不然分数是1）
clf.support_vectors_         #返回支持向量的坐标（说白了就是在-1和1的超平面线上的点）
clf.n_support_               #返回在两个分类下的支持向量个数

6、如果数据是环形呢？

环形数据如果使用线性SVM进行分类，效果非常的差，引出核函数。

x,y=make_circles(n_samples=50,factor=0.1,random_state=0,noise=0.1)
plt.scatter(x[:,0],x[:,1],c=y,s=50,cmap='rainbow')
plt.show()

五、核函数

1、概述

核函数可以将m维空间的内积运算转化为低维空间的核函数计算，从而解决了在高维特征空间上计算“维度诅咒”的灾难。

在Sklearn中就是参数kernel，常用的核函数有Linear线性，poly多项式，rbf径向基核函数，sigmoid核函数等。

常见的核函数计算公式：

线性核函数： $k(x,y)=x^Ty+c$

多项式核函数： $k(x,y)=(ax^Ty+c)^d$

径向基核函数： $k(x,y)=exp(-\gamma||x-y||^2)=exp(-\frac{||x-y||^2}{2\sigma^2})$

Sigmoid核函数： $k(x,y)=tanh(ax^T+c)$

不同核函数的特点：

线性核函数：简单，求解快，奥卡姆剃刀，可解释性强

多项式核函数：可解决非线性问题，参数较多，对大数量级特征不适用

径向基核函数：可以映射到无限维，决策边界更多样，只有一个参数，更容易选择，特征多时会选用。但可解释性差，容易过拟合，计算速度较慢。

Sigmoid核函数：主要用于神经网络。

如果发现径向基核函数，在多特征下效果不明显，可以descripe数据集，数据集可能有量纲不统一或者偏态问题，可以对数据集进行归一化处理，使数据集保证正态分布。

2、在不同类型数据集下使用不同核函数，进行可视化

2.1建立不同类型数据集

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap       #绘图
from sklearn.svm import SVC
from sklearn.datasets import make_circles ,make_moons,make_blobs,make_classificationn_samples=100
#建立月亮型，环形，聚类，二分类型数据集
datasets=[make_moons(n_samples=n_samples,noise=0.2,random_state=0),make_circles(n_samples=n_samples,noise=0.2,random_state=1),make_blobs(n_samples=n_samples,centers=2,random_state=5),make_classification(n_samples=n_samples,n_features=2,n_informative=2,n_redundant=0,random_state=5)#n_informative:相关特征 n_redundant:冗余特征
]

2.2建立20个子图

nrows=len(datasets)     #4
ncols=len(Kernel)+1     #5fig,axes=plt.subplots(nrows,ncols,figsize=(16,12))   #4行5列的20个子图

2.3使用不同核函数建模后可视化

for ds_cnt,(x,y) in enumerate(datasets):#第一层循环，绘制数据集的分散情况ax=axes[ds_cnt,0]if ds_cnt ==0:                   #只在第一列的第一个图上添加标题ax.set_title('Input data')ax.scatter(x[:,0],x[:,1],c=y,zorder=10,cmap=plt.cm.Paired,edgecolors='k')    #plt.cm.Paired配对颜色映射,对比度极强ax.set_xticks(())ax.set_yticks(())#第二层循环，在不同核函数下进行循环，绘图在第二列到第五列for est_idx,kernel in enumerate(Kernel):#定义子图位置ax=axes[ds_cnt,est_idx+1]#建立模型svc,计算评分clf=SVC(kernel=kernel,gamma=2).fit(x,y)score=clf.score(x,y)#绘制数据本身分布散点图ax.scatter(x[:,0],x[:,1],c=y,zorder=10,cmap=plt.cm.Paired,edgecolors='k')#绘制支持向量ax.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1],s=50,facecolors='none',zorder=10,edgecolors='k')#绘制决策边界x_min, x_max = x[:, 0].min() - .5, x[:, 0].max() + .5   #决策边界略大于所有的点围成的区域边界y_min, y_max = x[:, 1].min() - .5, x[:, 1].max() + .5#若干个坐标点,mgrid合并了linspace和meshgrid，表示为[min,max,step]xx,yy=np.mgrid[x_min:x_max:200j,y_min:y_max:200j]#np.c_类似于np.vstackz=clf.decision_function(np.c_[xx.ravel(),yy.ravel()]).reshape(xx.shape)#填充等高线不同颜色ax.pcolormesh(xx,yy,z>0,cmap=plt.cm.Paired)#绘制等高线ax.contour(xx,yy,z,colors='k',linestyles=['--','-','--'],levels=[-1,0,1])#坐标轴不显示ax.set_xticks(())ax.set_yticks(())#在第一行的图上打标签if ds_cnt == 0 :ax.set_title(kernel)#在图上加评分ax.text(0.95,0.06,('%.2f'%score).lstrip('0'),size=15,bbox=dict(boxstyle='round',alpha=0.8,facecolor='white'),   #填充白色0.8透明度圆框transform=ax.transAxes,                                    #保证坐标轴为原来坐标轴horizontalalignment='right')                               #水平靠右
plt.tight_layout()    #紧密排布子图
plt.show()

3、核函数调参

核函数调参一般有gamma，degree，coef0三个参数，对于不同核函数在三个参数上也有不同的影响。

input	表达式	gamma	degree	coef0
'linear'	$k(x,y)=x^Ty$	No	No	No
'poly'	$k(x,y)=(\gamma x^Ty+r)^d$	Yes	Yes	Yes
'sigmoid'	$k(x,y)=tanh(\gamma x^T+r)$	Yes	No	Yes
'rbf'	$k(x,y)=e^{(-\gamma\|\|x-y\|\|^2)}$	Yes	No	No

其中除了线性核函数以外，其他核函数还要受到gamma（ $\gamma$ ），degree(d)，coef0(常数r）的影响。

参数	含义
degree	整数，可不填，默认为3
gamma	浮点数，可不填，默认为'auto' 输入‘auto’，使用1/n_features 输入‘scale’，使用1/（n_features*x.std()）输入‘auto_deprecated’,表明没有传递明确gamma值
coef0	浮点数，可不填，默认为0.0