这里写自定义目录标题
- 参考资料
- 比较和分类
- 基础知识
- 16.3 有模型学习
- 16.3.1 策略评估
- 递归形式:Bellman 等式
- 16.3.2 策略改进
- 16.3.3 策略迭代
- 16.3.3 值迭代
- 16.4 免模型学习
- on-policy off-policy
- 16.4.1 蒙特卡罗强化学习
- 16.4.2 时序差分学习
- Sarsa算法:同策略算法(on-policy):行为策略是目标策略
- Q-learning算法:异策略算法(off-policy):行为策略不是目标策略
- 多步时序差分:无偏且方差小
- 16.5 值函数近似
- 16.6 模仿学习
- 16.6.1 直接模仿学习
- 16.6.2 逆强化学习(inverse RL)
- 生成式对抗模仿学习(generative adversarial imitation learning,GAIL)
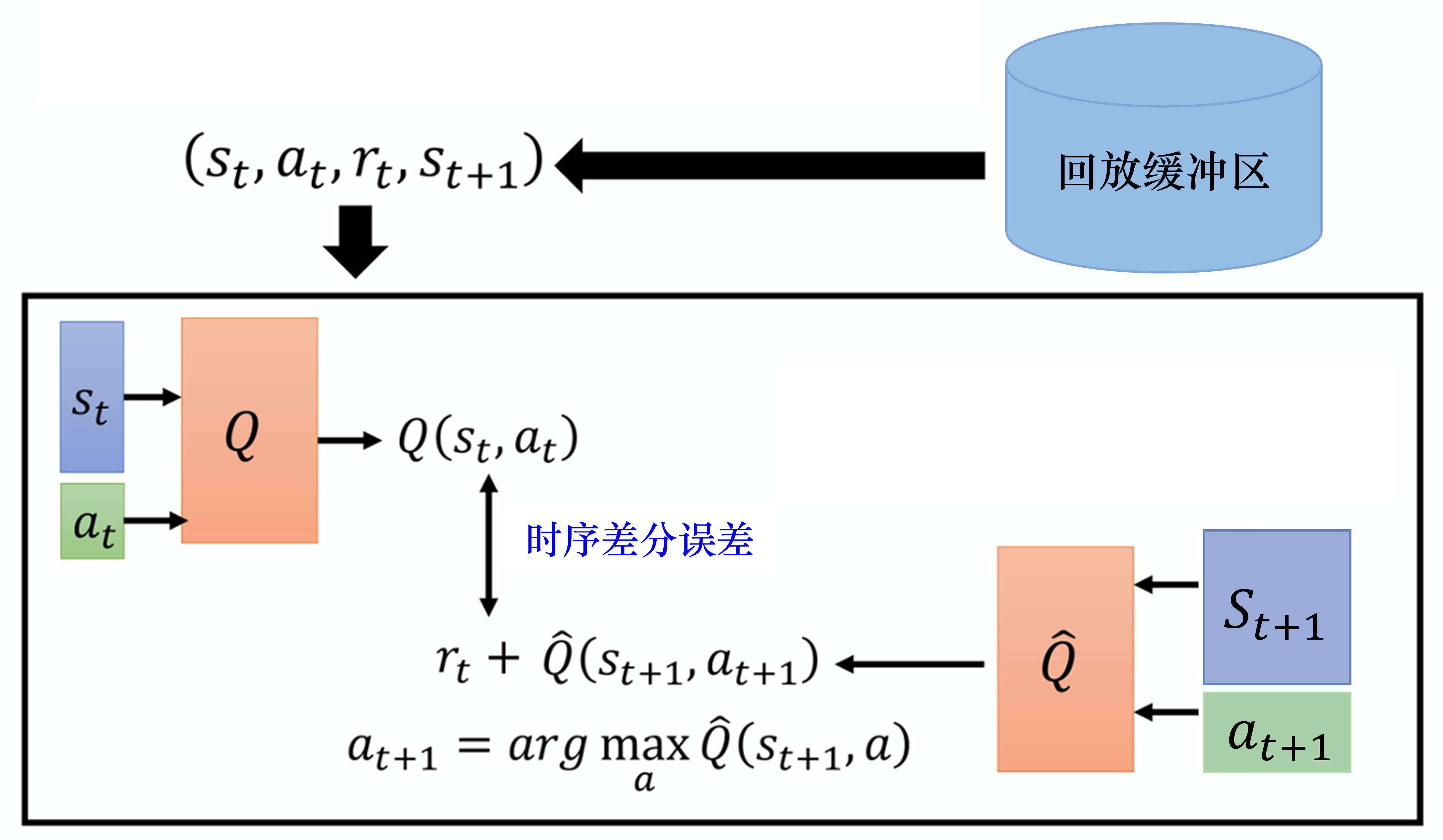
- 深度Q网络算法
- 经验回放(experience replay)
- 目标网络(target network)
- deep Q network, DQN
- Double Deep Q-Network
- 优先级经验回放 (prioritized experience replay, PER)
- Dueling Deep Q-Network
- 策略梯度 Policy Gradients
- REINFORCE:蒙特卡洛策略梯度
- Actor-Critic
- Advantage Actor-Critic
- 时序差分残差 Actor-Critic
- Asynchronous Advantage Actor-Critic (A3C)
- 路径衍生策略梯度(pathwise derivative policy gradient)
- 深度Q网络→路径衍生策略梯度
- Actor-Critic and GAN
- 信赖域策略优化 (Trust Region Policy Optimization, TRPO)
- 近端策略优化(proximal policy optimization,PPO)
- PPO-惩罚(PPO-Penalty)
- PPO-截断(PPO-Clip)
- 深度确定性策略梯度 (Deep Deterministic Policy Gradient, DDPG)
- 双延迟深度确定性策略梯度(twin delayed DDPG,TD3)
- 截断的双 Q 学习(clipped double Q-learning)
- 延迟的策略更新(delayed policy updates)
- 目标策略平滑(target policy smoothing)
- Soft Actor-Critic
- 目标导向的强化学习(goal-oriented reinforcement learning,GoRL)
- 多智能体强化学习(multi-agent reinforcement learning,MARL)
- 多智能体 DDPG(muli-agent DDPG,MADDPG)
- 应用案例:用户关联和信道分配
- a stochastic game
- Multi-Agent Q-Learning Method
- Multi-Agent dueling double DQN Algorithm
- 应用案例:分布式动态下行链路波束成形
- Limited-Information Exchange Protocol
- Distributed DRL-Based DTDE Scheme for DDBC
- Distributed DRL-Based DTDE Scheme for DDBC
参考资料
《机器学习》周志华
《机器学习》(西瓜书)公式详解
南瓜书PumpkinBook
Reinforcement Learning: An Introduction
second edition
Richard S. Sutton and Andrew G. Barto
incompleteideas代码
张尚彤代码
周沫凡强化学习
周沫凡强化学习代码
周沫凡Python tutorial
张伟楠,沈键,俞勇
动手学强化学习
动手学强化学习代码
蘑菇书
王琦,杨毅远,江季,Easy RL:强化学习教程,人民邮电出版社,2022.
Easy RL:强化学习教程
面向非地面网络的智能无线资源管理机制与算法研究
[1]曹阳. 面向非地面网络的智能无线资源管理机制与算法研究[D]. 电子科技大学, 2023. DOI: 10.27005/d.cnki.gdzku.2023.000168.
波束成形论文代码
中文整理的强化学习资料
https://hunch.net/~beygel/deep_rl_tutorial.pdf
https://icml.cc/2016/tutorials/deep_rl_tutorial.pdf
Tutorial: Deep Reinforcement Learning
David Silver, Google DeepMind
我的笔记2020年简书
我的笔记2020年CSDN
比较和分类
on-policy算法的采样效率比较低。
下表的算法全是model-free
| 算法 | 回合更新/单步更新 | on-policy / off-policy | Policy-Based / Value-Based | 策略 | 状态 | 动作 |
|---|---|---|---|---|---|---|
| Monte Carlo | 回合更新 | on-policy / off-policy | ||||
| Sarsa | 单步更新 | on-policy | Value-Based | 离散 | 离散 | |
| Q learning | 单步更新 | off-policy | Value-Based | 离散 | 离散 | |
| DQN | 单步更新 | off-policy | Value-Based | 连续 | 离散 | |
| Policy Gradients | 回合更新→单步更新 | on-policy | Policy-Based | 随机 | 连续 | |
| REINFORCE | 回合更新 | on-policy | Policy-Based | 随机 | 连续 | |
| Actor-Critic | 可以单步更新 | on-policy | Policy-Based / Value-Based | |||
| TRPO | on-policy | 随机 | ||||
| PPO | on-policy | 随机 | ||||
| DDPG | 单步更新 | off-policy | 确定 | 连续 | ||
| Soft Actor-Critic | off-policy | Policy-Based / Value-Based | 随机 |
actor会基于概率做出动作。
critic会对做出的动作给出动作的价值。
基础知识
以单智能体强化学习为例,具体的MDP数学模型M可以概括为M={S,A,R,P},其中,S,A,R和P分别表示智能体的状态集合、动作集合,奖励函数集合和状态转移概率集合。
强化学习任务对应了四元组 E= (X,A,P,R)
- 状态空间X
- 动作空间A
- 状态转移概率P:X×A×X→实数域
- 奖赏R:X×A×X→实数域
确定性策略:a=π(x),即在状态x下执行a动作;
随机性策略:P=π(x,a),即在状态x下执行a动作的概率。
π ( a ∣ s ) = p [ A t = a ∣ S t = s ] \pi(a|s)=p[A_t=a|S_t=s] π(a∣s)=p[At=a∣St=s]
强化学习在某种意义上可看作具有“延迟标记信息”的监督学习问题
K-摇臂赌博机
仅探索法:将尝试的机会平均分给每一个动作,即轮流执行,最终将每个动作的平均奖赏作为期望奖赏的近似值。
仅利用法:将尝试的机会分给当前平均奖赏值最大的动作。
欲累积奖赏最大,则必须在探索与利用之间达成较好的折中
ε-贪心法:基于一个概率来对探索和利用进行折中
以概率ε进行探索:πε(s) = 以均匀概率从A中选取动作
以概率1-ε进行利用:πε(s) = π(s) = a r g m a x a Q ( s , a ) argmax_{a} Q(s,a) argmaxaQ(s,a),即选择当前最优的动作。
Softmax算法:基于当前每个动作的平均奖赏值来对探索和利用进行折中
τ趋于0时, Softmax 将趋于“仅利用”
τ趋于无穷大时, Softmax 将趋于“仅探索”
16.3 有模型学习
有模型学习:状态空间、动作空间、转移概率以及奖赏函数都已经给出
预测(prediction)和控制(control)是马尔可夫决策过程里面的核心问题。
预测(评估一个给定的策略)的输入是马尔可夫决策过程 <S,A,P,R,γ> 和策略π,输出是价值函数Vπ。
控制(搜索最佳策略)的输入是马尔可夫决策过程 <S,A,P,R,γ>,输出是最佳价值函数(optimal value function)V∗和最佳策略(optimal policy)π∗。
16.3.1 策略评估
折扣累积回报: G t = R t + 1 + γ R t + 2 + ⋯ = ∑ k = 0 ∞ γ k R t + k + 1 G_t=R_{t+1}+\gamma R_{t+2}+\cdots =\sum_{k=0}^{\infty}{\gamma^kR_{t+k+1}} Gt=Rt+1+γRt+2+⋯=∑k=0∞γkRt+k+1
状态值函数(V):Vπ(x),即从状态x出发,使用π策略所带来的累积奖赏;
υ π ( s ) = E π [ G t ∣ S t = s ] = E π [ ∑ k = 0 ∞ γ k R t + k + 1 ∣ S t = s ] \upsilon_{\pi}\left(s\right)=E_{\pi}\left[{G_t|S_t=s}\right] =E_{\pi}\left[\sum_{k=0}^{\infty}{\gamma^kR_{t+k+1}|S_t=s}\right] υπ(s)=Eπ[Gt∣St=s]=Eπ[∑k=0∞γkRt+k+1∣St=s]
状态值函数V表示执行策略π能得到的累计折扣奖励:
V π ( s ) = E [ R ( s 0 , a 0 ) + γ R ( s 1 , a 1 ) + γ 2 R ( s 2 , a 2 ) + γ 3 R ( s 3 , a 3 ) + … ∣ s = s 0 ] V^π(s) = E[R(s_0,a_0)+γR(s_1,a_1)+γ^2R(s_2,a_2)+γ^3R(s_3,a_3)+…|s=s_0] Vπ(s)=E[R(s0,a0)+γR(s1,a1)+γ2R(s2,a2)+γ3R(s3,a3)+…∣s=s0]
V π ( s ) = R ( s , a ) + γ ∑ s ′ ∈ S p ( s ′ ∣ s , π ( s ) ) V π ( s ′ ) V^{\pi}(s)=R(s, a)+\gamma \sum_{s^{\prime} \in S} p\left(s^{\prime} | s, \pi(s)\right) V^{\pi}\left(s^{\prime}\right) Vπ(s)=R(s,a)+γ∑s′∈Sp(s′∣s,π(s))Vπ(s′)
状态-动作值函数(Q):Qπ(x,a),即从状态x出发,执行动作a后再使用π策略所带来的累积奖赏。
q π ( s , a ) = E π [ G t ∣ S t = s , A t = a ] = E π [ ∑ k = 0 ∞ γ k R t + k + 1 ∣ S t = s , A t = a ] q_{\pi}\left(s,a\right)=E_{\pi}\left[{G_t|S_t=s,A_t=a}\right] =E_{\pi}\left[\sum_{k=0}^{\infty}{\gamma^kR_{t+k+1}|S_t=s,A_t=a}\right] qπ(s,a)=Eπ[Gt∣St=s,At=a]=Eπ[∑k=0∞γkRt+k+1∣St=s,At=a]
状态动作值函数Q(s,a)表示在状态s下执行动作a能得到的累计折扣奖励:
Q π ( s , a ) = E [ R ( s 0 , a 0 ) + γ R ( s 1 , a 1 ) + γ 2 R ( s 2 , a 2 ) + γ 3 R ( s 3 , a 3 ) + … ∣ s = s 0 , a = a 0 ] Q^π(s,a) = E[R(s_0,a_0)+γR(s_1,a_1)+γ^2R(s_2,a_2)+γ^3R(s_3,a_3)+…|s=s_0,a=a_0] Qπ(s,a)=E[R(s0,a0)+γR(s1,a1)+γ2R(s2,a2)+γ3R(s3,a3)+…∣s=s0,a=a0]
Q π ( s , a ) = R ( s , a ) + γ ∑ s ′ ∈ S p ( s ′ ∣ s , π ( s ) ) Q π ( s ′ , π ( s ′ ) ) Q^{\pi}(s, a)=R(s, a)+\gamma \sum_{s^{\prime} \in S} p\left(s^{\prime} | s, \pi(s)\right) Q^{\pi}\left(s^{\prime}, \pi\left(s^{\prime}\right)\right) Qπ(s,a)=R(s,a)+γ∑s′∈Sp(s′∣s,π(s))Qπ(s′,π(s′))
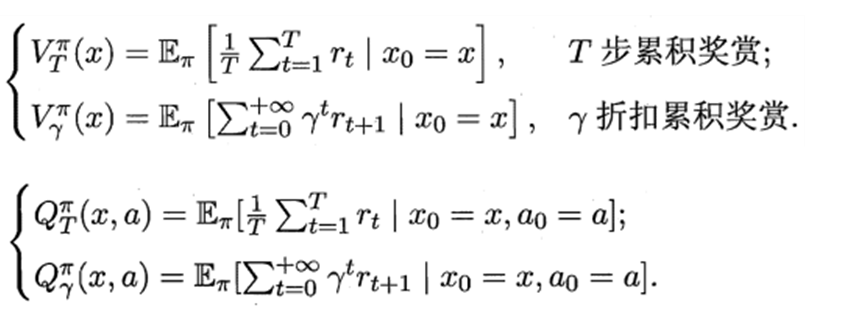
递归形式:Bellman 等式
状态值函数的Bellman方程:
υ ( s ) = E [ G t ∣ S t = s ] = E [ R t + 1 + γ R t + 2 + ⋯ ∣ S t = s ] = E [ R t + 1 + γ ( R t + 2 + γ R t + 3 + ⋯ ) ∣ S t = s ] = E [ R t + 1 + γ G t + 1 ∣ S t = s ] = E [ R t + 1 + γ υ ( S t + 1 ) ∣ S t = s ] \upsilon(s)=E[G_t|S_t=s] \\ =E[R_{t+1}+\gamma R_{t+2}+\cdots |S_t=s] \\ =E[R_{t+1}+\gamma(R_{t+2}+\gamma R_{t+3}+\cdots)|S_t=s] \\ =E[R_{t+1}+\gamma G_{t+1}|S_t=s] \\ =E[R_{t+1}+\gamma\upsilon(S_{t+1})|S_t=s] υ(s)=E[Gt∣St=s]=E[Rt+1+γRt+2+⋯∣St=s]=E[Rt+1+γ(Rt+2+γRt+3+⋯)∣St=s]=E[Rt+1+γGt+1∣St=s]=E[Rt+1+γυ(St+1)∣St=s]
状态动作值函数的Bellman方程:
q π ( s , a ) = E π [ G t ∣ S t = s , A t = a ] = E π [ R t + 1 + γ q ( S t + 1 , A t + 1 ) ∣ S t = s , A t = a ] q_{\pi}(s,a)=E_{\pi}[G_t|S_t=s,A_t=a]\\ =E_{\pi}[R_{t+1}+\gamma q(S_{t+1},A_{t+1})|S_t=s,A_t=a] qπ(s,a)=Eπ[Gt∣St=s,At=a]=Eπ[Rt+1+γq(St+1,At+1)∣St=s,At=a]
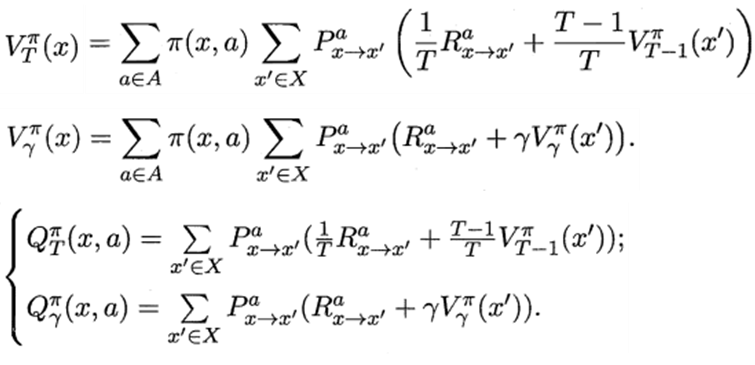
16.3.2 策略改进
最优策略:使得值函数对所有状态求和的值最大的策略
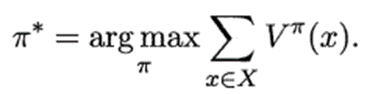
最优值函数:最优策略对应的值函数
策略改进: π ′ ( s ) = argmax a ∈ A Q π ( s , a ) \pi^{'}(s)=\underset{a∈A}{\operatorname{argmax}} Q^{\pi}(s, a) π′(s)=a∈AargmaxQπ(s,a)
π ∗ ( s ) = argmax a Q ∗ ( s , a ) \pi^{*}(s)=\underset{a}{\operatorname{argmax}} Q^{*}(s, a) π∗(s)=aargmaxQ∗(s,a)
16.3.3 策略迭代
策略迭代:不断迭代进行策略评估和策略改进,直到策略收敛、不再改变为止

16.3.3 值迭代
值迭代:不断迭代进行策略评估,直到值函数收敛、不再改变为止

16.4 免模型学习
在原始策略上使用ε-贪心策略
ε-贪心法:基于一个概率来对探索和利用进行折中
以概率ε进行探索:πε(s) = 以均匀概率从A中选取动作
以概率1-ε进行利用:πε(s) = π(s) = a r g m a x a Q ( s , a ) argmax_{a} Q(s,a) argmaxaQ(s,a),即选择当前最优的动作。
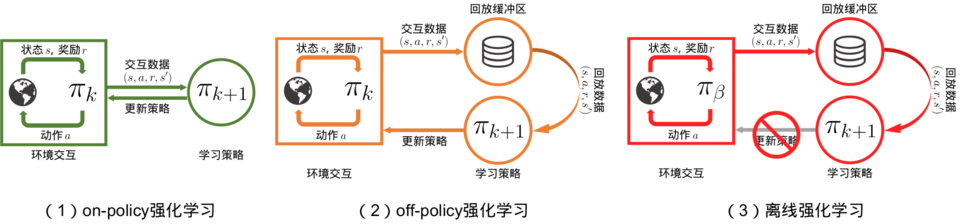
on-policy off-policy
the target policy: the policy being learned about
the behavior policy: the policy used to generate behavior
In this case we say that learning is from data “off” the target policy, and the overall process is termed off-policy learning.
目标策略:正在被学习的策略。要学习的智能体。代理和环境交互过程中所选择的动作
行为策略:被用来产生行为的策略。与环境交互的智能体。计算评估函数的过程中选择的动作
同策略(on-policy):行为策略是目标策略
要学习的智能体和与环境交互的智能体相同
智能体直接采用正在优化的策略函数收集训练数据,即利用自身在特定时间内产生的连续决策轨迹更新当前的DNN参数。
异策略(off-policy):行为策略不是目标策略。
要学习的智能体和与环境交互的智能体不相同
智能体在收集训练数据时采用与正在优化的策略函数不一致的策略。
智能体在训练过程中可以不断和环境交互,得到新的反馈数据。
on-policy算法:直接使用这些反馈数据
off-policy算法:先将数据存入经验回放池中,需要时再采样。
离线强化学习(offline reinforcement learning):在智能体不和环境交互的情况下,仅从已经收集好的确定的数据集中,通过强化学习算法得到比较好的策略。
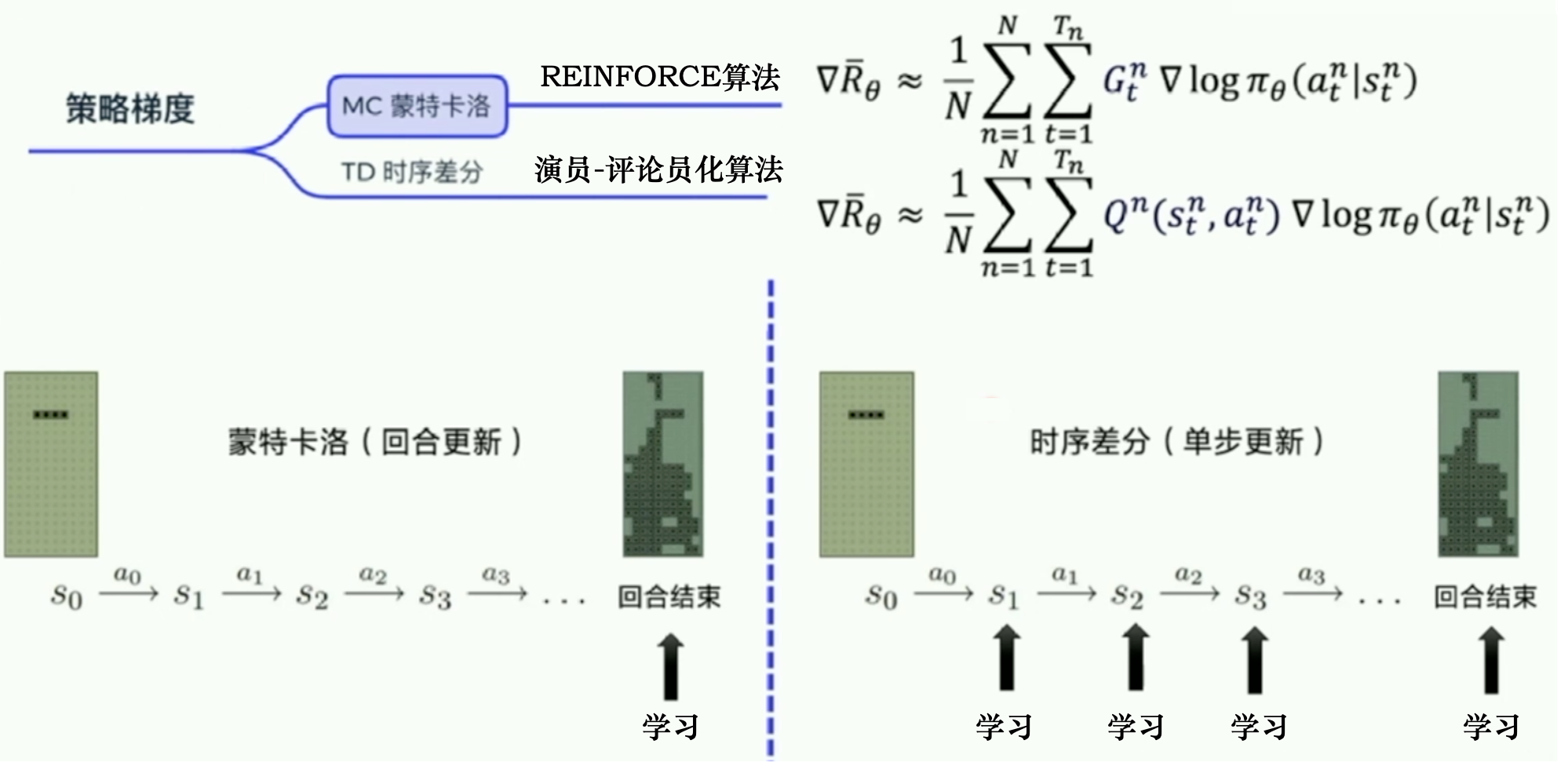
16.4.1 蒙特卡罗强化学习
蒙特卡罗强化学习:通过采样来进行策略评估。
多次“采样”,然后求取平均累积奖赏来作为期望累积奖赏的近似
由于采样必须为有限次数,因此该方法更适合于使用 步累积奖赏的强化学习任务。
估计状态-动作值函数

同策略(on-policy)蒙特卡罗强化学习算法:被评估和被改进的都是同一个策略
异策略(off-policy)蒙特卡罗强化学习算法:仅在评估时使用ε-贪心策略,而在改进时使用原始策略
蒙特卡罗强化学习算法没有充分利用强化学习任务的 MDP 结构
16.4.2 时序差分学习
蒙特卡罗强化学习算法在一个完整的采样轨迹完成后再对所有的状态-动作对进行更新。
实际上这个更新过程能增量式进行。
时序差分(Temporal Difference ,简称 TD )学习则结合了动态规划与蒙特卡罗方法的思想,能做到更高效的免模型学习。
Sarsa算法:同策略算法(on-policy):行为策略是目标策略
每次更新值函数需知道前一步的状态(state)x、前一步的动作(action)a、奖赏值(reward)R、当前状态(state)x’、将要执行的动作(action)a’:
Q ( s , a ) ← Q ( s , a ) + α [ R + γ Q ( s ′ , a ′ ) − Q ( s , a ) ] , γ ∈ [ 0 , 1 ) Q(s,a)←Q(s,a)+\alpha[R+\gamma Q\left(s^{\prime}, a^{\prime}\right)-Q(s,a)],\gamma∈[0,1) Q(s,a)←Q(s,a)+α[R+γQ(s′,a′)−Q(s,a)],γ∈[0,1)
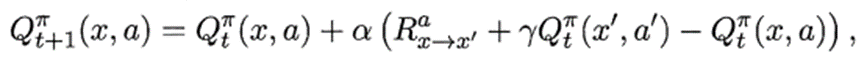
更新步长α越大,则越靠后的累积奖赏越重要。
π(s) = a r g m a x a Q ( s , a ) argmax_{a} Q(s,a) argmaxaQ(s,a)

on policy 同策略
在选择动作执行的时候采取的策略 = 在更新Q表的时候采取的策略
行为策略 行动策略是ε-greedy策略
目标策略 评估策略是ε-greedy策略
Q-learning算法:异策略算法(off-policy):行为策略不是目标策略
每次更新值函数需知道前一步的状态(state)x、前一步的动作(action)a、奖赏值(reward)R、当前状态(state)x’
Q值表:state为行,action为列,reward为元素
Q ( s , a ) ← Q ( s , a ) + α [ R + γ max a ′ Q ( s ′ , a ′ ) − Q ( s , a ) ] , γ ∈ [ 0 , 1 ) Q(s,a)←Q(s,a)+\alpha[R+\gamma \max _{a^{\prime}} Q\left(s^{\prime}, a^{\prime}\right)-Q(s,a)],\gamma∈[0,1) Q(s,a)←Q(s,a)+α[R+γmaxa′Q(s′,a′)−Q(s,a)],γ∈[0,1)
学习率*(Q的真实值 - Q的估计值)
如果学习率越大,那么新估计值代替旧估计值的程度也越大

off-policy 异策略
在选择动作执行的时候采取的策略 ≠ 在更新Q表的时候采取的策略
行为策略 行动策略是ε-greedy策略
目标策略 更新Q表的策略是贪婪策略
Q-learning的目标策略不管行为策略会产生什么动作。Q-learning的目标策略默认下一个动作就是 Q 值最大的那个动作,并且默认按照最佳的策略去优化目标策略,所以它可以更大胆地去寻找最优的路径,它表现得比 Sarsa 大胆得多。
异策略算法的这个循环可以拆开成2个部分:与环境交互(执行动作,获得奖励和观察状态)和学习(用动作,奖励,状态更新Q),从而实现离线学习。
离线学习的行为策略一直没更新,训练效果应该也不好?
多步时序差分:无偏且方差小
蒙特卡洛方法利用当前状态之后每一步的奖励而不使用任何价值估计
时序差分算法只利用一步奖励和下一个状态的价值估计。
蒙特卡洛方法:无偏(unbiased),方差大
方差大,因为每一步的状态转移都有不确定性,而每一步状态采取的动作所得到的不一样的奖励最终都会加起来,这会极大影响最终的价值估计;
时序差分算法:有偏,方差小
方差小,因为只关注了一步状态转移,用到了一步的奖励
有偏,因为用到了下一个状态的价值估计而不是其真实的价值。
多步时序差分可以结合二者的优势
多步sarsa
Sarsa(0):Sarsa 是一种单步更新法, 在环境中每走一步, 更新一次自己的行为准则。等走完这一步以后直接更新行为准则
Sarsa(1):走完这步, 再走一步, 然后再更新
Sarsa(n):如果等待回合完毕我们一次性再更新呢, 比如这回合我们走了 n 步
Sarsa(lambda):有了一个 lambda 值来代替我们想要选择的步数
lambda 是脚步衰减值, 是一个在 0 和 1 之间的数
当 lambda 取0, 就变成了 Sarsa 的单步更新
当 lambda 取 1, 就变成了回合更新, 对所有步更新的力度都是一样
当 lambda 在 0 和 1 之间, 取值越大, 离宝藏越近的步更新力度越大
16.5 值函数近似
直接对连续状态空间的值函数进行学习
值函数能表达为状态的线性函数
线性值函数近似 Sarsa 算法
线性值函数近似 Q-learning算法
16.6 模仿学习
模仿学习
假设存在一个专家智能体,其策略可以看成最优策略,我们就可以直接模仿这个专家在环境中交互的状态动作数据来训练一个策略,并且不需要用到环境提供的奖励信号。
逆强化学习(inverse RL)
16.6.1 直接模仿学习
直接模仿人类专家的“状态-动作对"
行为克隆(behavior cloning,BC)
直接使用监督学习方法,将专家数据(状态,动作)中的状态看作样本输入,动作视为标签
16.6.2 逆强化学习(inverse RL)
逆强化学习:从人类专家提供的范例数据中反推出奖赏函数
生成式对抗模仿学习(generative adversarial imitation learning,GAIL)
2016 年由斯坦福大学研究团队提出的基于生成式对抗网络的模仿学习
它诠释了生成式对抗网络的本质其实就是模仿学习。
深度Q网络算法
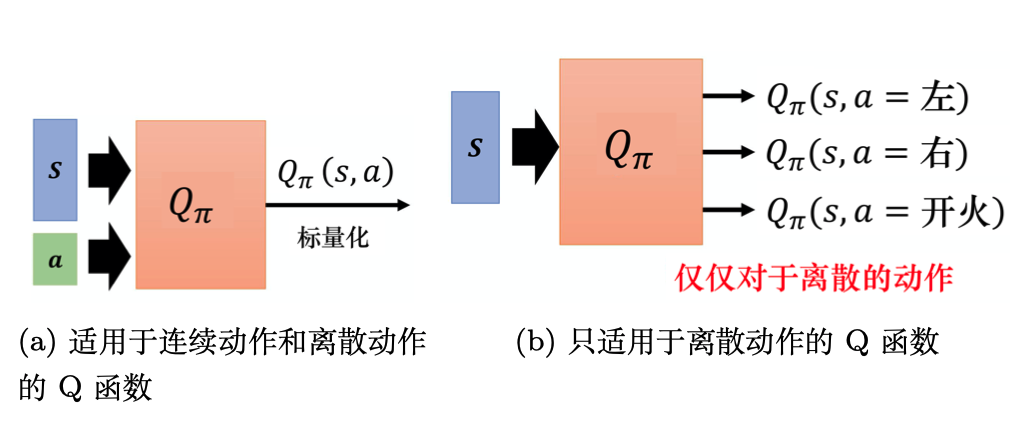
Q-learning算法:状态离散,动作离散,并且空间都比较小的情况下适用
若动作是连续(无限)的,神经网络的输入:状态s和动作a。输出:在状态s下采取动作a能获得的价值。
若动作是离散(有限)的,除了可以采取动作连续情况下的做法,我们还可以:神经网络的输入:状态s。输出:每一个动作的Q值。
通常 DQN(以及 Q-learning)只能处理动作离散的情况,因为在Q函数的更新过程中有max_a这一操作。
Q网络:用于拟合Q函数的神经网络
用权重为w的Q网络 Q ( s , a , w ) Q(s,a,w) Q(s,a,w)表示value函数 Q ∗ ( s , a ) Q^∗(s,a) Q∗(s,a)
DQN 算法最终更新的目标:最小化损失函数
Q 网络的损失函数构造为均方误差的形式:
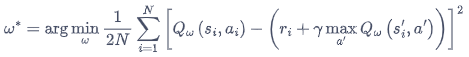
I = ( r + γ max a Q ( s ′ , a ′ , w ) − Q ( s , a , w ) ) 2 I=\left(r+\gamma \max _{a} Q\left(s^{\prime}, a^{\prime}, \mathbf{w}\right)-Q(s, a, \mathbf{w})\right)^{2} I=(r+γmaxaQ(s′,a′,w)−Q(s,a,w))2
经验回放(experience replay)
如果某个算法使用了经验回放,该算法就是off-policy算法。
维护一个回放缓冲区,将每次从环境中采样得到的四元组数据(状态、动作、奖励、下一状态)存储到回放缓冲区中,训练 Q 网络的时候再从回放缓冲区中随机采样若干数据来进行训练。
好处:
- 打破样本之间的相关性,让其满足独立假设。
在 MDP 中交互采样得到的数据本身不满足独立假设,因为这一时刻的状态和上一时刻的状态有关。
非独立同分布的数据对训练神经网络有很大的影响,会使神经网络拟合到最近训练的数据上。
回放缓冲区里面的经验来自于不同的策略,我们采样到的一个批量里面的数据会是比较多样的。 - 提高样本效率。
每一个样本可以被使用多次,十分适合深度神经网络的梯度学习。
与环境交互比较慢,训练网络比较快。
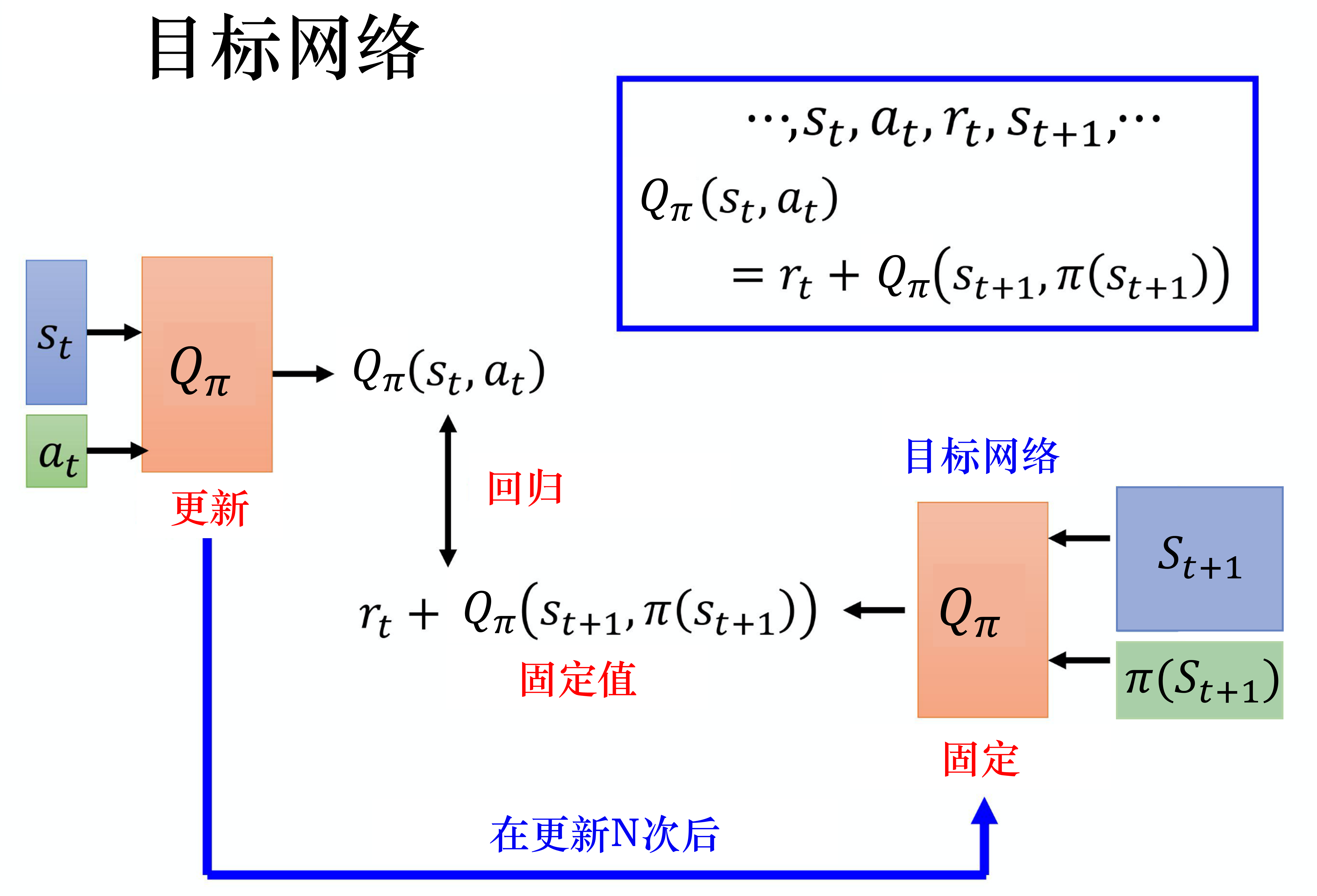
目标网络(target network)
损失函数包含神经网络的输出,因此在更新网络参数的同时目标也在不断地改变,这容易造成神经网络训练的不稳定性。
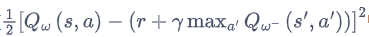
训练网络:用于计算损失函数的前一项,并且使用正常梯度下降方法来进行更新。
目标网络:用于计算损失函数的后一项 r + γ max a ′ Q ( s ′ , a ′ , w − ) r+\gamma \max _{a'} Q\left(s^{\prime}, a^{\prime}, \mathbf{w}-\right) r+γmaxa′Q(s′,a′,w−)
训练网络在训练中的每一步都会更新。
目标网络的参数每隔几步才会与训练网络同步一次。
这样做使得目标网络相对于训练网络更加稳定。
deep Q network, DQN


Double Deep Q-Network
[1509.06461] Deep Reinforcement Learning with Double Q-learning
DQN的问题:DQN算法通常会导致对Q值的过高估计
DQN:Q_next = max(Q_next(s’, a_all))
Y t D Q N ≡ R t + 1 + γ max a Q ( S t + 1 , a ; θ t − ) Y_{t}^{\mathrm{DQN}} \equiv R_{t+1}+\gamma \max _{a} Q\left(S_{t+1}, a ; \boldsymbol{\theta}_{t}^{-}\right) YtDQN≡Rt+1+γmaxaQ(St+1,a;θt−)
Double DQN:Q_next = Q_next(s’, argmax(Q_eval(s’, a_all)))
Y t DoubleDQN ≡ R t + 1 + γ Q ( S t + 1 , argmax a Q ( S t + 1 , a ; θ t ) ; θ t − ) Y_{t}^{\text {DoubleDQN }} \equiv R_{t+1}+\gamma Q\left(S_{t+1}, \underset{a}{\operatorname{argmax}} Q\left(S_{t+1}, a ; \boldsymbol{\theta}_{t}\right); \boldsymbol{\theta}_{t}^{-}\right) YtDoubleDQN ≡Rt+1+γQ(St+1,aargmaxQ(St+1,a;θt);θt−)
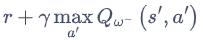
DQN的优化目标为 ,动作的选取依靠目标网络
,动作的选取依靠目标网络
Double DQN 的优化目标为 ,动作的选取依靠训练网络
,动作的选取依靠训练网络
用训练网络计算使Q值最大的动作
用目标网络计算Q值
当前的Q网络w用于选择动作
旧的Q网络w−用于评估动作
I = ( r + γ Q ( s ′ , argmax a ′ Q ( s ′ , a ′ , w ) , w − ) − Q ( s , a , w ) ) 2 I=\left(r+\gamma Q\left(s^{\prime}, \underset{a^{\prime}}{\operatorname{argmax}} Q\left(s^{\prime}, a^{\prime}, \mathbf{w}\right), \mathbf{w}^{-}\right)-Q(s, a, \mathbf{w})\right)^{2} I=(r+γQ(s′,a′argmaxQ(s′,a′,w),w−)−Q(s,a,w))2
Double DQN 的代码实现可以直接在 DQN 的基础上进行,无须做过多修改。
优先级经验回放 (prioritized experience replay, PER)
[1511.05952] Prioritized Experience Replay
Double Learning and Prioritized Experience Replay
重视值得学习的样本
时序差分误差 = 网络的输出与目标之间的差距
如果采样过的数据的时序差分误差特别大,那么应该让它们以比较大的概率被采样到。

batch 抽样的时候并不是随机抽样, 而是按照 Memory 中的样本优先级来抽
用到 TD-error, 也就是 Q现实 - Q估计 来规定优先学习的程度
如果 TD-error 越大, 就代表我们的预测精度还有很多上升空间, 那么这个样本就越需要被学习, 也就是优先级 p 越高
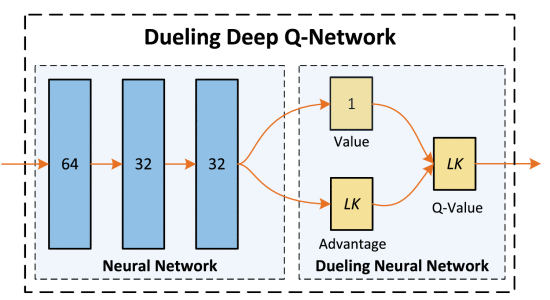
Dueling Deep Q-Network
[1511.06581] Dueling Network Architectures for Deep Reinforcement Learning
Dueling DQN 能够很好地学习到不同动作的差异性,在动作空间较大的环境下非常有效。
动作状态价值函数 = 状态价值函数 + 优势函数
将Q网络分成2个通道
Q η , α , β ( s , a ) = V η , α ( s ) + A η , β ( s , a ) Q_{\eta, \alpha, \beta}(s,a) = V_{\eta, \alpha}(s) + A_{\eta, \beta}(s,a) Qη,α,β(s,a)=Vη,α(s)+Aη,β(s,a)
V η , α ( s ) V_{\eta, \alpha}(s) Vη,α(s):状态价值函数,与action无关
A η , β ( s , a ) A_{\eta, \beta}(s,a) Aη,β(s,a):该状态下采取不同动作的优势函数,与action有关
η \eta η是状态价值函数和优势函数共享的网络参数,一般用在神经网络中,用来提取特征的前几层
α \alpha α和 β \beta β分别为状态价值函数和优势函数的参数。
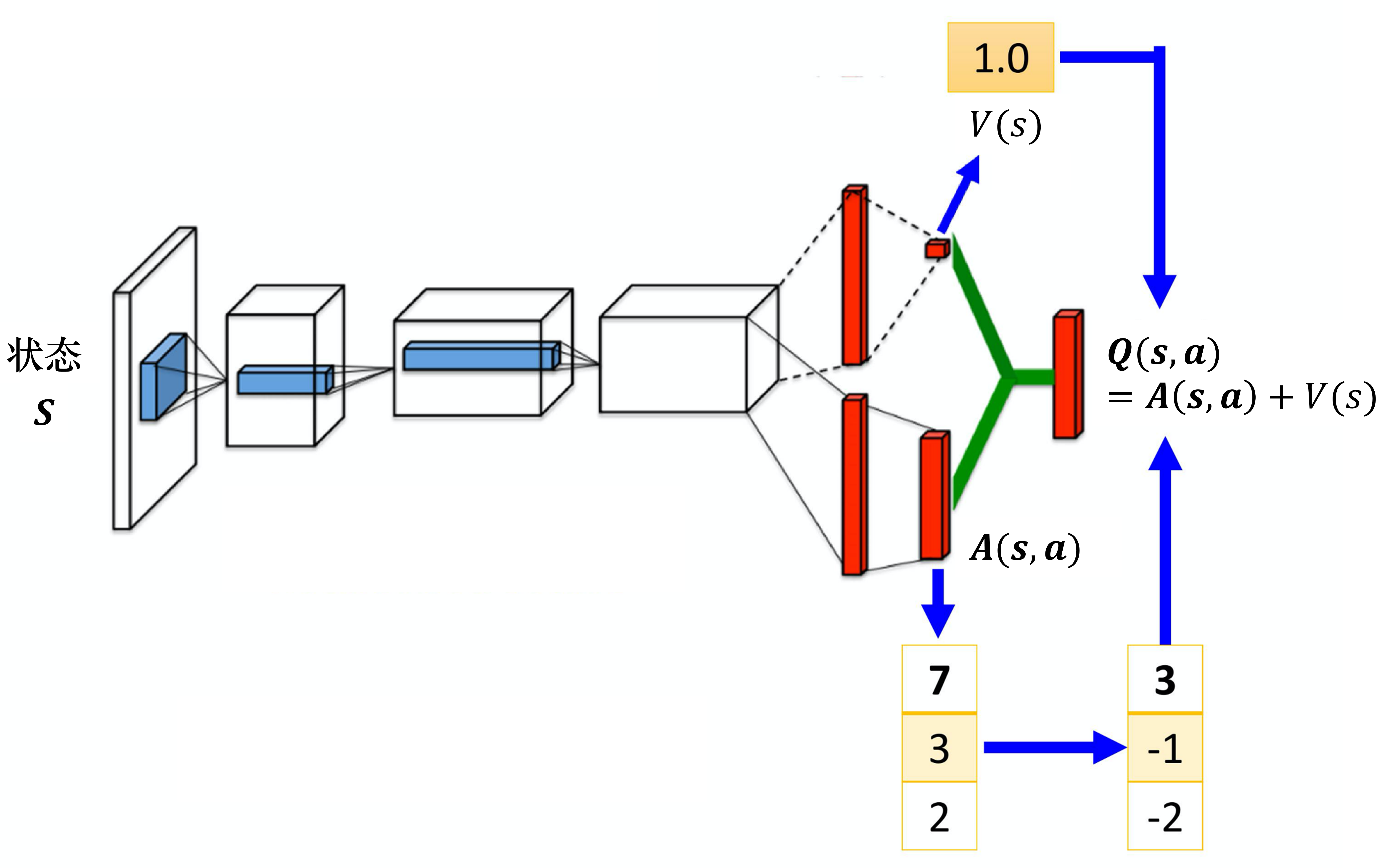
竞争深度Q网络的问题:最后学习的结果可能是这样的:
智能体就学到V(s)等于0,A(s,a)等于Q,就和原来的深度Q网络一样。
解决方案:在把A(s,a)与V(s)加起来之前,先处理A(s,a)。比如减去均值
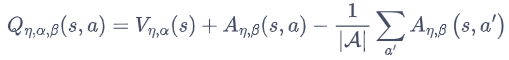
虽然它不再满足bellman最优方程,但实际应用时更加稳定。
策略梯度 Policy Gradients
基于值函数的方法:学习值函数,然后根据值函数导出一个策略。学习过程中并不存在一个显式的策略
基于策略的方法:直接显式地学习一个目标策略。
policy gradient要输出不是action的value,而是具体的那一个action,跳过了value这个阶段。输出的这个action可以是一个连续的值。
优点:连续动作
在策略梯度中,梯度可以写成一般的形式:
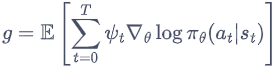
其中, ψ t \psi_t ψt可以有很多种形式

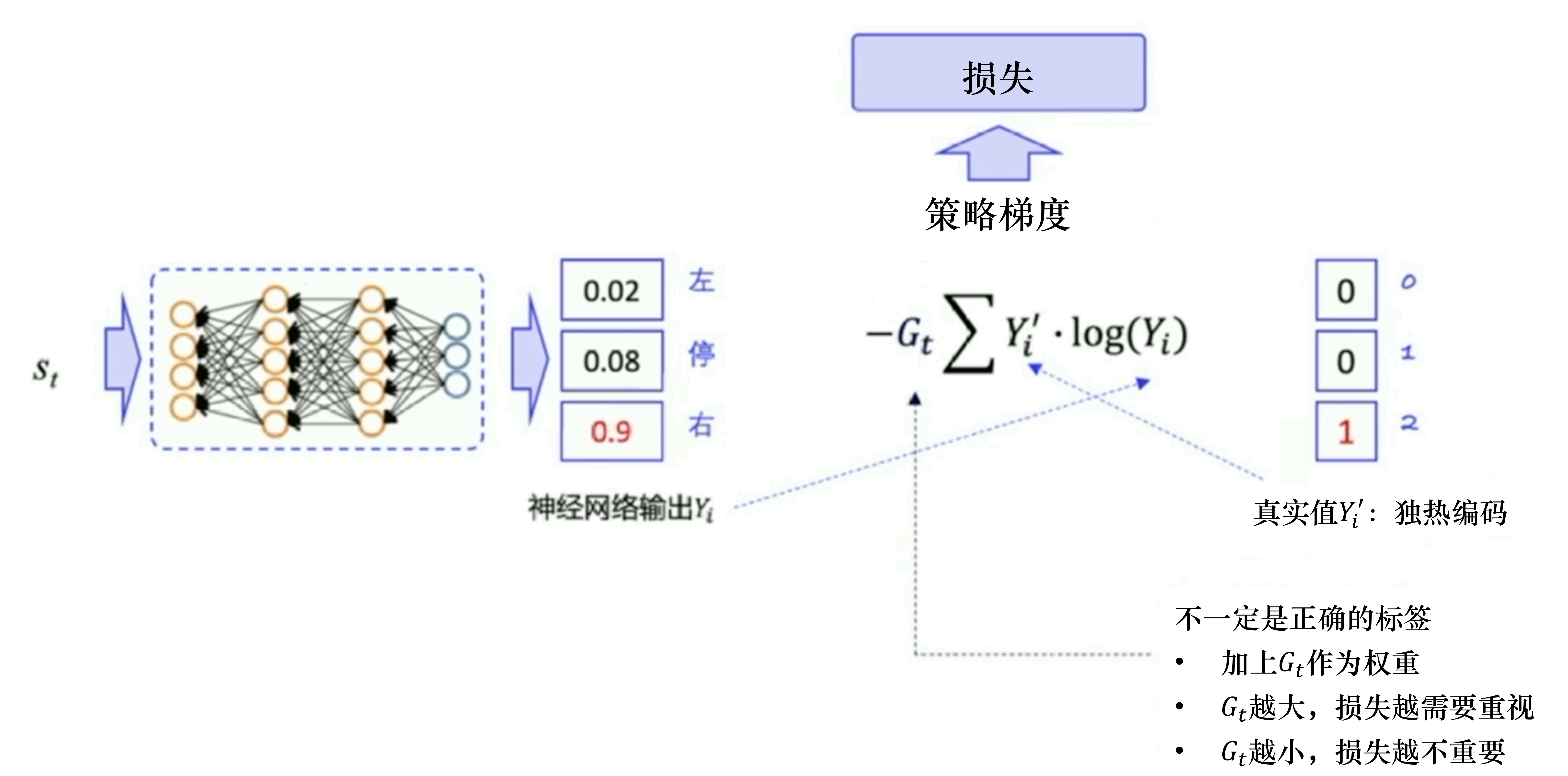
最小化损失 → 最大化Y’=1对应的那个Y
REINFORCE:蒙特卡洛策略梯度
Gt:从第t步开始,往后能够获得的总奖励

REINFORCE 算法
1.用一个策略模型来输出动作概率。通过 sample() 函数得到一个具体的动作,与环境交互,得到整个回合的数据。
2.执行 learn() 函数,用这些数据去构造损失函数,“扔”给优化器优化,更新策略模型。
在状态s对所选动作a的吃惊度:delta(log(Policy(s,a)) * V)
Policy(s,a)概率越小,-log(Policy(s,a))(即-log§)越大
如果Policy(s,a)很小时,拿到的R大,即V大,那-delta(log(Policy(s,a)) * V)就更大,表示更吃惊。(选了一个不常选的动作,却发现它能得到的reward很大,那么大幅修改参数)
因为使用了蒙特卡洛方法,REINFORCE算法的缺点:回合更新
1.梯度估计的方差很大
2.只能在序列结束后进行更新,这同时也要求任务具有有限的步数
Actor-Critic算法则可以在每一步之后都进行更新,并且不对任务的步数做限制。
Actor-Critic
Actor-Critic算法既学习价值函数,又学习策略函数
本质上是基于策略的算法,因为这一系列算法的目标都是优化一个带参数的策略,只是会额外学习价值函数,从而帮助策略函数更好地学习。
Actor-Critic有演员网络和评论家网络。
- Actor使用策略梯度函数:生成动作并与环境交互。
策略函数,描述状态和离散动作或连续动作分布的映射关系。
在Critic价值函数的指导下用策略梯度学习一个更好的策略。 - Critic使用价值函数:评估Actor的表现,并在下一阶段指导Actor的行为。
传统的值函数,来评估不同状态下的收益
通过Actor与环境交互收集的数据学习一个价值函数,这个价值函数会用于判断在当前状态什么动作是好的,什么动作不是好的。
它可以加速策略梯度函数的收敛,但这还不足以解决复杂的问题。
结合了Policy Gradient (Actor)和Function Approximation (Critic)的方法
Actor基于概率选行为
Critic基于Actor的行为评判行为的得分
Actor根据Critic的评分修改选行为的概率
Actor 在运用 Policy Gradient 的方法进行 Gradient ascent 的时候, 由 Critic 来告诉他, 这次的 Gradient ascent 是不是一次正确的 ascent。如果这次的得分不好, 那么就不要 ascent 那么多
Actor-Critic的优势:可以进行单步更新,比传统的Policy Gradient要快。
Actor-Critic的劣势:取决于Critic的价值判断,但是Critic难收敛,再加上Actor的更新,就更难收敛。
Advantage Actor-Critic
Q π ( s , a ) = V π ( s ) + A π ( s , a ) Q^\pi(s,a) = V^\pi(s) + A^\pi(s,a) Qπ(s,a)=Vπ(s)+Aπ(s,a)
A π ( s , a ) = Q π ( s , a ) − V π ( s ) A^\pi(s,a)= Q^\pi(s,a) - V^\pi(s) Aπ(s,a)=Qπ(s,a)−Vπ(s)
Advantage Actor-Critic采用了优势函数
缺点:需要估计2个网络:Q网络和 V网络。估计不准的风险变成原来的两倍。
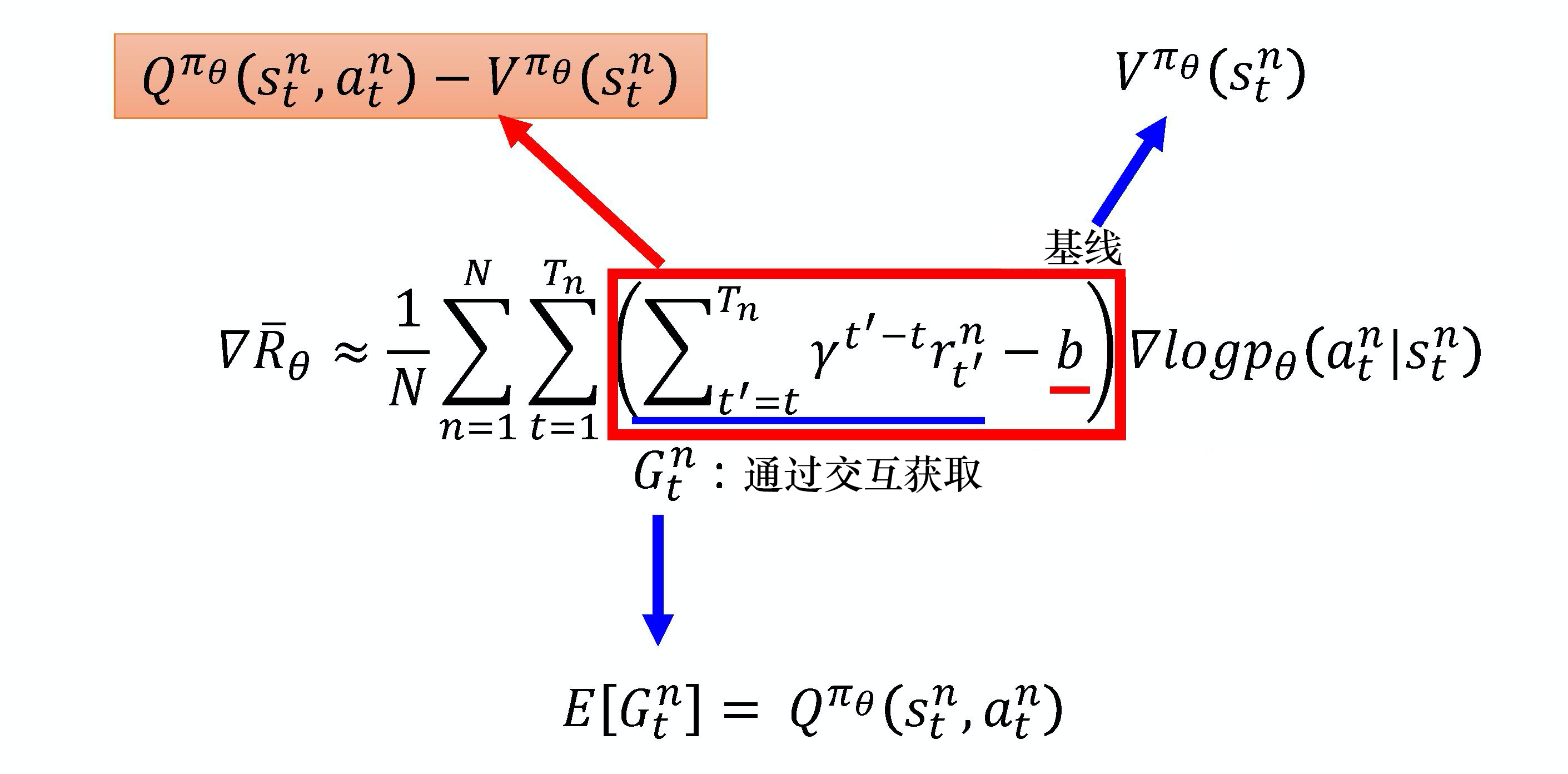
时序差分残差 Actor-Critic
A π ( s t , a t ) = Q π ( s t , a t ) − V π ( s t ) A^\pi(s_{t}, a_{t})= Q^\pi(s_{t}, a_{t}) - V^\pi(s_{t}) Aπ(st,at)=Qπ(st,at)−Vπ(st)
用 r t + γ V π ( s t + 1 ) r_{t}+ \gamma V^\pi(s_{t+1}) rt+γVπ(st+1)替换 Q π ( s t , a t ) Q^\pi(s_{t}, a_{t}) Qπ(st,at)得到
r t + γ V π ( s t + 1 ) − V π ( s t ) r_{t}+ \gamma V^\pi(s_{t+1}) - V^\pi(s_{t}) rt+γVπ(st+1)−Vπ(st)
不需要估计Q,只需要估计V
引入一个随机的参数r,r的方差小于G的方差
Critic网络Vπ(s)接收一个状态,输出一个标量。
Actor的策略π(s)接收一个状态,
如果动作是离散的,输出就是一个动作的分布。
如果动作是连续的,输出就是一个连续的向量。
Actor网络和Critic网络的输入都是s,所以它们前面几个层(layer)是可以共享的。
Asynchronous Advantage Actor-Critic (A3C)
[1602.01783] Asynchronous Methods for Deep Reinforcement Learning
异步优势演员-评论员算法
不同于经验回放,异步优势演员评论家在环境的多个实例上异步地并行执行多个代理。这种并行性还去相关代理的数据,变成一个更加平稳的过程中,因为在任何给定的时间步,并行代理都会经历各种不同的状态。
A3C同时使用很多个进程(worker),每一个进程就像一个影分身,最后这些影分身会把所有的经验值集合在一起。
如果CPU少,那么不好实现A3C,但可以实现Advantage Actor-Critic。

路径衍生策略梯度(pathwise derivative policy gradient)
路径衍生策略梯度
可以看成一种特别的DQN方法,解连续动作
可以看成一种特别的Actor-Critic方法
原来的Actor-Critic的问题:Critic只告诉Actor好或不好的,没有告诉Actor什么样是好。
Critic会直接告诉Actor什么动作才是好的。
- 策略π与环境交互并估计Q值。
- 固定Q值,只去学习一个Actor。假设这个Q值估得很准,它知道在某一个状态采取什么样的动作会得到很大的Q值。
接下来就学习这个Actor,Actor在给定s的时候,采取了a,可以让最后Q函数算出来的值越大越好。
我们用准则(criteria)去更新策略π

深度Q网络→路径衍生策略梯度

Actor-Critic and GAN
Connecting Generative Adversarial Network and Actor-Critic Methods
| Actor-Critic | GAN 生成对抗网络 | |
|---|---|---|
| Actor 演员 | generator 生成器 | |
| Critic 评论员 | discriminator 判别器 |

信赖域策略优化 (Trust Region Policy Optimization, TRPO)
基于策略的方法:参数化智能体的策略,并设计衡量策略好坏的目标函数,通过梯度上升的方法来最大化这个目标函数,使得策略最优。
策略梯度算法的缺点:当策略网络是深度模型时,沿着策略梯度更新参数,很有可能由于步长太长,策略突然显著变差,进而影响训练效果。
TRPO算法优点:在理论上能够保证策略学习的性能单调性。
在 2015 年被提出
近端策略优化(proximal policy optimization,PPO)
TRPO算法的缺点:计算过程非常复杂,每一步更新的运算量非常大。
OpenAI提出的一种解决Policy Gradient不好确定Learning rate(或者Step size)的问题
因为如果step size过大,学出来的Policy会一直乱动,不会收敛
如果Step Size太小,对于完成训练,收敛时间太长
PPO利用New Policy和Old Policy的比例,限制了New Policy的更新幅度,让Policy Gradient对稍微大点的Step size不那么敏感。
PPO-惩罚(PPO-Penalty)
PPO-截断(PPO-Clip)
深度确定性策略梯度 (Deep Deterministic Policy Gradient, DDPG)
动作连续、off-policy、确定性策略(目标策略),单步更新
确定性策略:a=π(x),即在状态x下执行a动作;
随机性策略:P=π(x,a),即在状态x下执行a动作的概率。
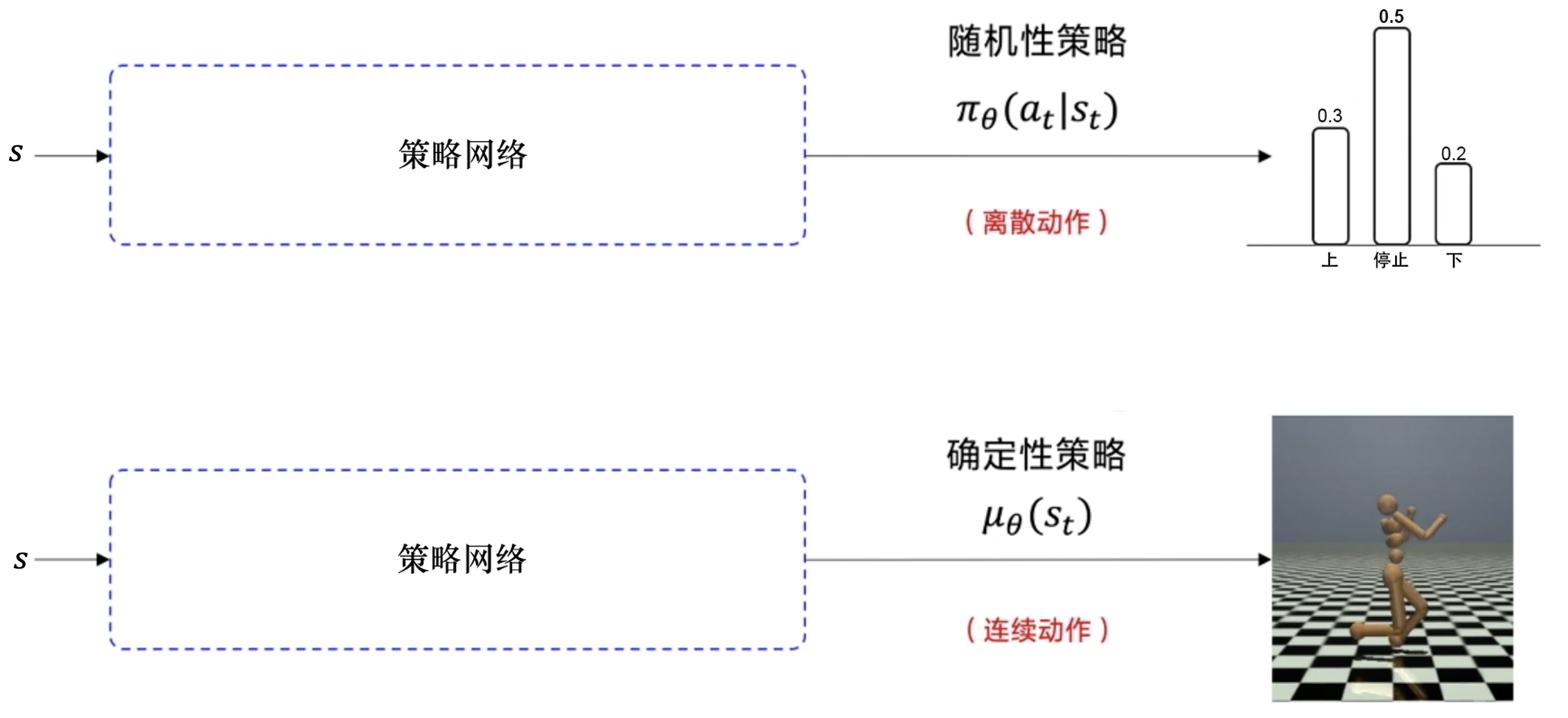
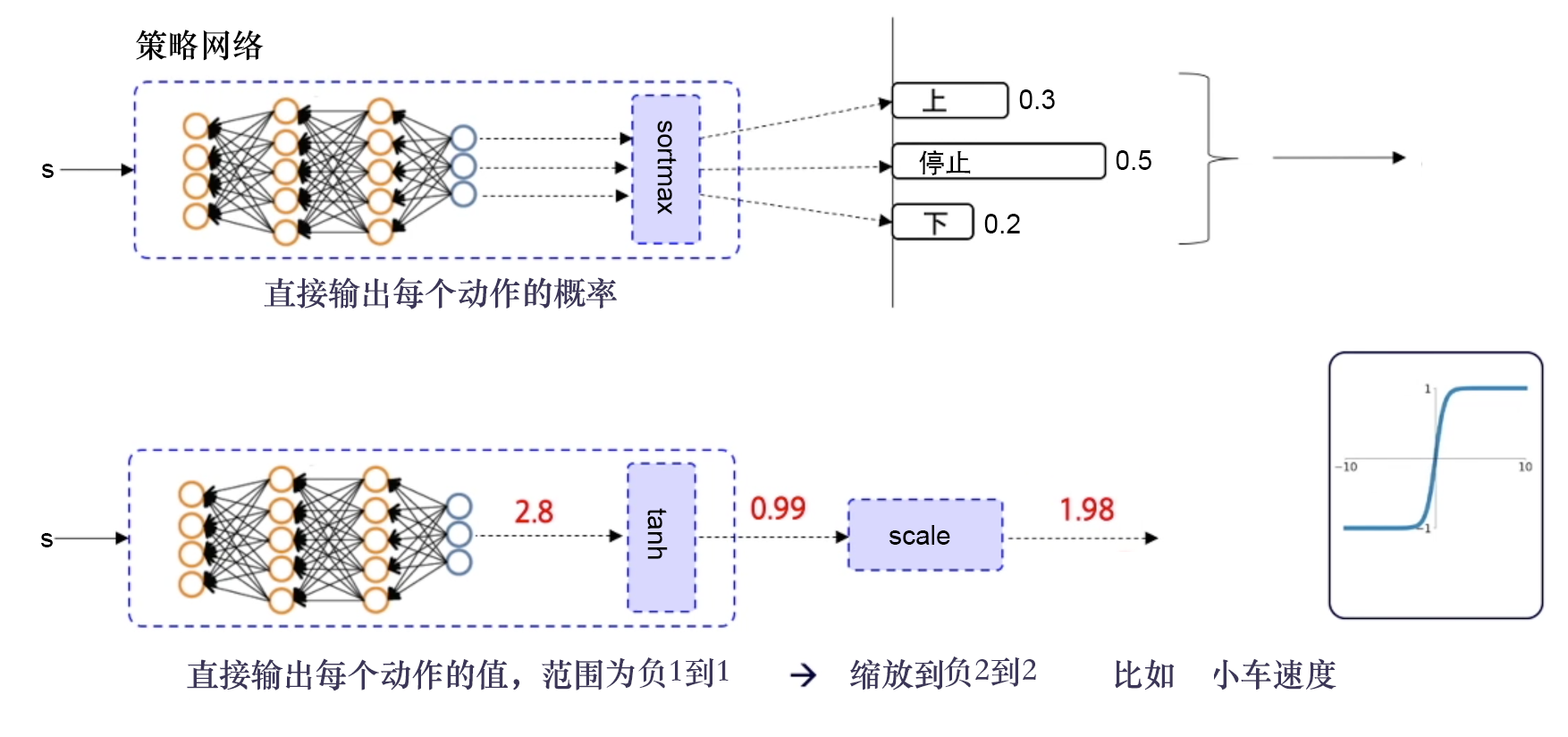
输出离散动作,加一层 softmax 层,确保所有的输出是动作概率,并且所有的动作概率和为 1。
输出连续动作,加一层 tanh 函数,把输出限制到 [−1,1],然后根据实际动作的范围将其缩放,再输出给环境。
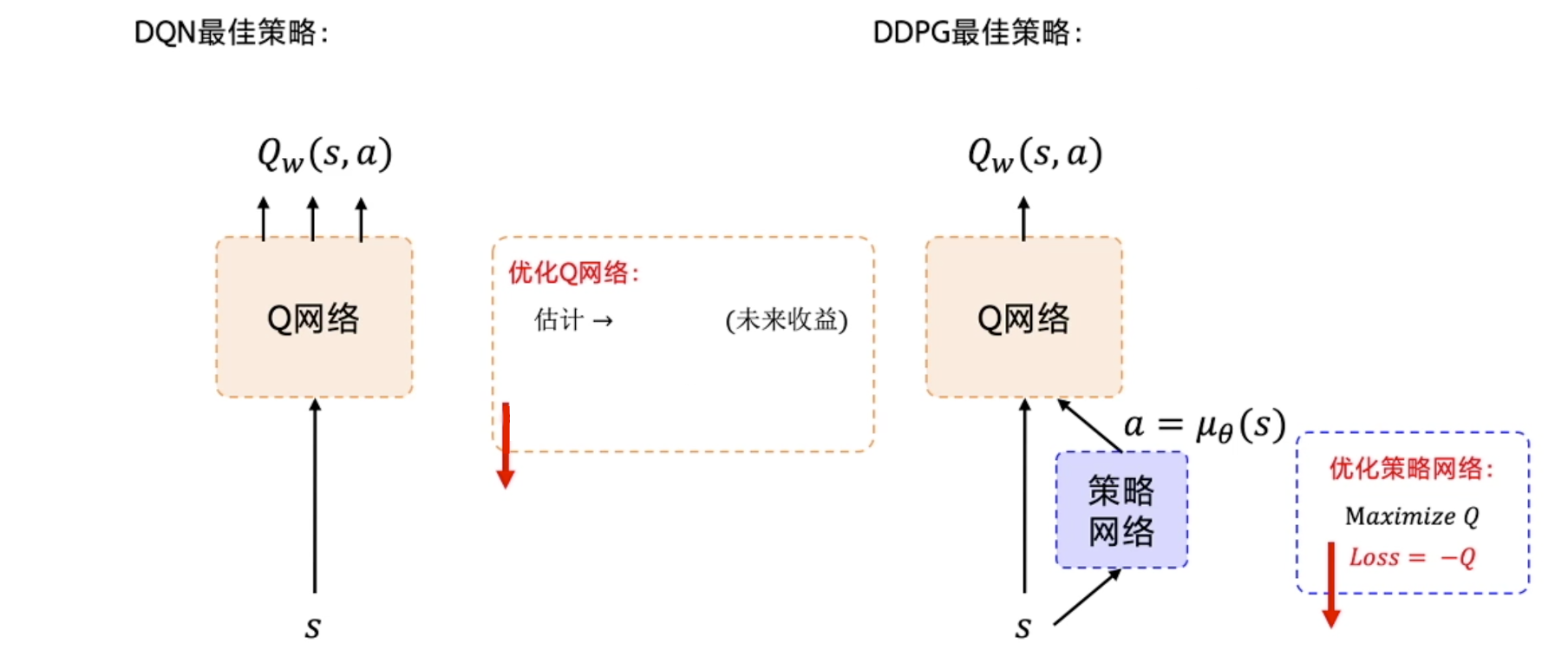
Google DeepMind提出的
使用Actor-Critic结构,结合了DQN结构的优势,提高了Actor-Critic的稳定性和收敛性。
由于有环境反馈的奖励存在,因此Critic的评分会越来越准确,所评判的Actor的表现也会越来越好。
优化策略网络的梯度:最大化Q值。损失函数:-Q。
优化Q网络:让Q网络的输出逼近Q_target。损失函数:Qw(s,a)和Q_target的均方差。
DDPG要用到4个神经网络,其中Actor和Critic各用1个网络,此外它们都各自有1个目标网络。
训练需要用到的数据:只需要s、a、r、s′
经验回放:用回放缓冲区把这些数据存起来,然后采样进行训练。经验回放的技巧与DQN中的是一样的。因为 DDPG 使用了经验回放技巧,所以 DDPG 是off-policy。
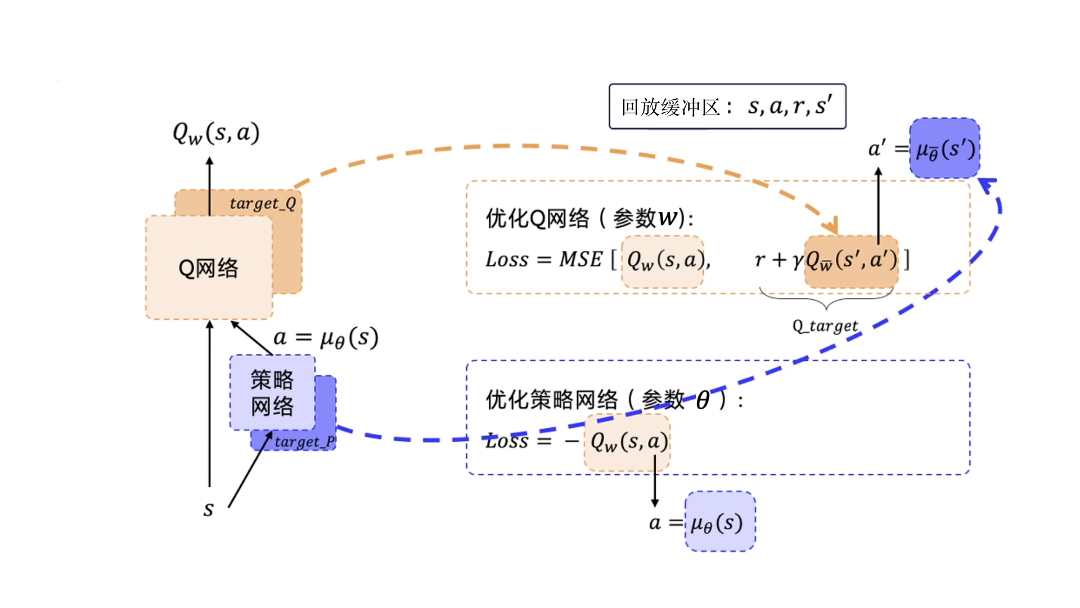
目标网络的更新
软更新: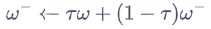
在DQN中,τ=1,即每隔一段时间将Q网络直接复制给目标Q网络;
在DDPG中,τ<1,目标Q网络逐渐接近Q网络。目标μ网络也使用这种软更新的方式。
DDPG采用了Double DQN中的技术来更新Q网络。
由于DDPG采用的是确定性策略,它本身的探索仍然十分有限。
DQN算法的探索:行为策略采用贪婪策略
DDPG算法的探索:行为策略引入随机噪声。不相关的、均值为 0 的高斯噪声

双延迟深度确定性策略梯度(twin delayed DDPG,TD3)
双延迟深度确定性策略梯度
TD3代码
DDPG对于超参数和其他类型的调整方面经常很敏感。
DDPG常见的问题:已经学习好的 Q 函数开始显著地高估 Q 值,导致策略被破坏,因为它利用了 Q 函数中的误差。
截断的双 Q 学习(clipped double Q-learning)
TD3通过最小化均方差来同时学习两个Q函数:Q ϕ 1 和 Q ϕ 2 。
2个Q函数都使用一个目标,2个Q函数中给出的较小的值会被作为 Q-target
延迟的策略更新(delayed policy updates)
以较低的频率更新动作网络,以较高的频率更新评价网络
通常每更新2次评价网络就更新1次策略。
目标策略平滑(target policy smoothing)
在目标动作中加入噪声,通过平滑 Q 沿动作的变化,使策略更难利用 Q 函数的误差。
Soft Actor-Critic
off-policy、随机性策略
比DDPG稳定
Soft Actor-Critic
DDPG 的训练非常不稳定,收敛性较差,对超参数比较敏感,也难以适应不同的复杂环境。
2018 年,一个更加稳定的算法 Soft Actor-Critic(SAC)被提出。
SAC 的前身是 Soft Q-learning,它们都属于最大熵强化学习的范畴。
Soft Q-learning 不存在一个显式的策略函数,而是使用一个函数的波尔兹曼分布,在连续空间下求解非常麻烦。为了解决这个问题,SAC 提出使用一个 Actor 表示策略函数。
最大熵强化学习(maximum entropy RL)的思想就是除了要最大化累积奖励,还要使得策略更加随机。如此,强化学习的目标中就加入了一项熵的正则项
熵正则化增加了强化学习算法的探索程度,α越大,探索性就越强,有助于加速后续的策略学习,并减少策略陷入较差的局部最优的可能性。
最大熵强化学习:通过控制策略所采取动作的熵来调整探索与利用的平衡

目标导向的强化学习(goal-oriented reinforcement learning,GoRL)
目标导向的强化学习
事后经验回放(hindsight experience replay,HER)算法于 2017 年神经信息处理系统(Neural Information Processing Systems,NeurIPS)大会中被提出,成为 GoRL 的一大经典方法。
多智能体强化学习(multi-agent reinforcement learning,MARL)
单智能体强化学习算法的基本假设:动态环境是稳态的(stationary),即状态转移概率和奖励函数不变。
多智能体强化学习要比单智能体更困难:
- 在每个智能体的视角下,环境是非稳态的(non-stationary),即对于一个智能体而言,即使在相同的状态下采取相同的动作,得到的状态转移和奖励信号的分布可能在不断改变;
- 多个智能体的训练可能是多目标的,不同智能体需要最大化自己的利益;
- 训练评估的复杂度会增加,可能需要大规模分布式训练来提高效率。
独立学习(independent learning):完全去中心化的算法
独立 PPO(Independent PPO,IPPO)算法
中心化训练去中心化执行(centralized training with decentralized execution,CTDE)
中心化训练:在训练的时候使用一些单个智能体看不到的全局信息而以达到更好的训练效果
去中心化执行:在执行时不使用这些信息,每个智能体完全根据自己的策略直接动作。
优点:能够在训练时有效地利用全局信息以达到更好且更稳定的训练效果,同时在进行策略模型推断时可以仅利用局部信息,使得算法具有一定的扩展性。
多智能体 DDPG(muli-agent DDPG,MADDPG)
每个智能体实现一个 DDPG 的算法。
所有智能体共享一个中心化的 Critic 网络,该 Critic 网络在训练的过程中同时对每个智能体的 Actor 网络给出指导,而执行时每个智能体的 Actor 网络则是完全独立做出行动,即去中心化地执行。

应用案例:用户关联和信道分配
N. Zhao, Y. -C. Liang, D. Niyato, Y. Pei, M. Wu and Y. Jiang, “Deep Reinforcement Learning for User Association and Resource Allocation in Heterogeneous Cellular Networks,” in IEEE Transactions on Wireless Communications, vol. 18, no. 11, pp. 5141-5152, Nov. 2019, doi: 10.1109/TWC.2019.2933417.
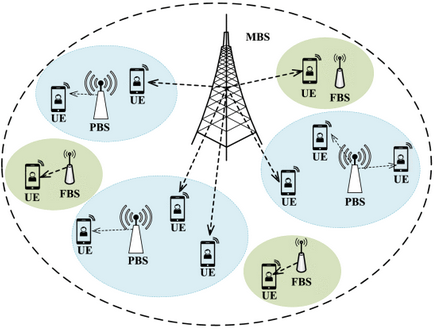
L BSs → N UEs
K orthogonal channels
the Joint user association and resource allocation Optimization Problem
variables: discrete
1.bli(t)=1: the i i ith UE chooses to associate with the BS l l l at time t t t
2.cik(t)=1: the i i ith UE utilizes the channel C k Ck Ck at time t t t
constraints
1.each UE can only choose at most one BS at any time
2.each UE can only choose at most one channel at any time
3.the SINR of the i t h ith ith UE ≥
a stochastic game
state
si(t) ∈{0, 1}
si(t)=0 means that the ith UE cannot meet its the minimum QoS requirement, that is, Γi(t) < Ωi
the number of possible states is 2 N 2^N 2N
action
alki(t)={bli(t),cik(t)},
1.bli(t)=1: the i i ith UE chooses to associate with the BS l l l at time t t t
2.cik(t)=1: the i i ith UE utilizes the channel C k Ck Ck at time t t t
The number of possible actions of each UE is L K LK LK = L种选择方式 * K种选择方式
reward
the long-term reward Φi = the weighted sum of the instantaneous rewards over a finite period T
the reward of the ith UE = the ith UE’s utility - the action-selection cost Ψi
Ψi > 0. Note that the negative reward (−Ψi) acts as a punishment.
to guarantee the minimum QoS of all UEs, this negative reward should be set big enough.
the ith UE’s utility = \rho_i * the total transmission capacity of the ith UE - the total transmission cost associated with the ith UE
Multi-Agent Q-Learning Method
At the beginning of each training episode, the network state is initialized through message passing.
- Each UE is connected to the neighboring BS with the maximum received signal power.
By using a pilot signal, each UE can measure the received power from the associated BS and the randomly-selected channel. - Then, each UE reports its own current state to its current associated BS.
By the message passing among the BSs through the backhaul communication link, the global state information of all UEs is obtained. - Then, the BSs send this global state informations to all UEs.
Each episode ends when the QoS of all UEs is satisfied or when the maximum step T is reached.
The total episode reward is the accumulation of instantaneous rewards of all steps within an episode.

Q i ( s , a i ) = Q i ( s , a i ) + δ [ u i ( s , a i , π − i ) + γ max a i ′ ∈ A i Q i ( s ′ , a i ′ ) − Q i ( s , a i ) [ u i ( s , a i , π − i ) + γ max a i ′ ∈ A i Q i ( s ′ , a i ′ ) ] , {Q_{i}}(s,a_{i})={Q_{i}}(s,a_{i})+ \delta \left[{ {u_{i}}(s,a_{i},{\mathcal{ \pi }}_{-i}) + \gamma \max \limits _{a_{i}' \in {\mathcal{ A}}_{i}} {Q_{i}}({s'},{a_{i}'})} {- {Q_{i}}(s,a_{i})\vphantom {\left [{ {u_{i}}(s,a_{i},{\mathcal{ \pi }}_{-i}) + \gamma \max \limits _{a_{i}' \in {\mathcal{ A}}_{i}} {Q_{i}}({s'},{a_{i}'})}\right.} }\right], Qi(s,ai)=Qi(s,ai)+δ[ui(s,ai,π−i)+γai′∈AimaxQi(s′,ai′)−Qi(s,ai)[ui(s,ai,π−i)+γai′∈AimaxQi(s′,ai′)],
Multi-Agent dueling double DQN Algorithm
dueling double deep Q-network (D3QN)
A NN function approximator Q i ( s , a i ; θ ) ≈ Q i ∗ ( s , a i ) Q_{i}(s,a_{i};{\theta }) \approx {Q_{i}^{*}}(s,a_{i}) Qi(s,ai;θ)≈Qi∗(s,ai) with weights θ is used as an online network.
The DQN utilizes a target network alongside the online network to stabilize the overall network performance.
experience replay
During learning, instead of using only the current experience (s, ai,ui(s, ai),s′), the NN can be trained through sampling mini-batches of experiences from replay memory D uniformly at random.
By reducing the correlation among the training examples, the experience replay strategy ensures that the optimal policy cannot be driven to a local minima.
double DQN
since the same values are used to select and evaluate an action in Q-learning and DQN methods, Q-value function may be over-optimistically estimated.
Thus, double DQN (DDQN) [44] is used to mitigate the above problem
dueling architecture
The advantage function A(s, ai) describes the advantage of the action ai compared with the other possible actions.
This dueling architecture can lead to better policy evaluation.
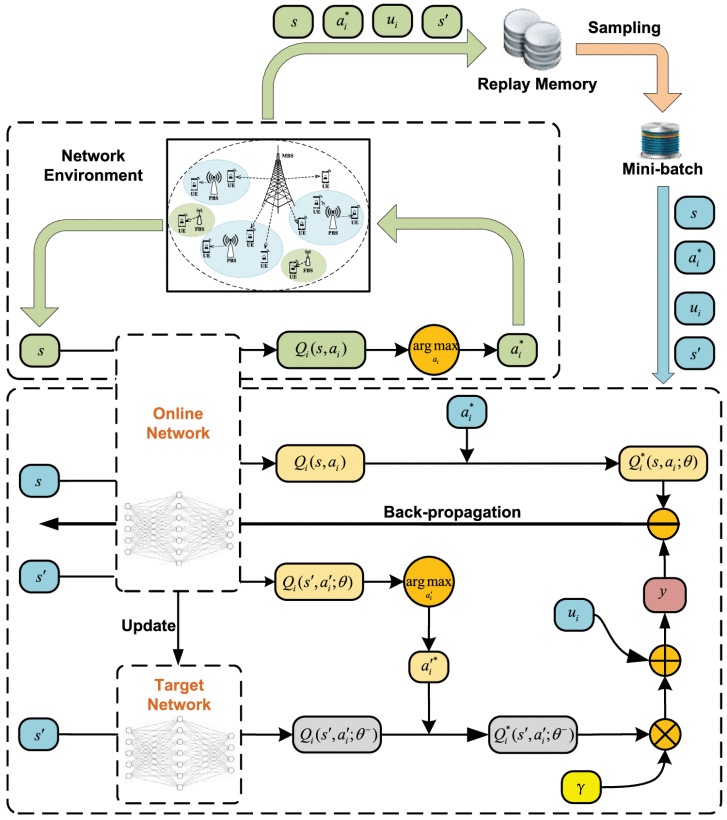
L i ( θ ) = E s , a i , u i ( s , a i ) , s ′ [ ( y i D Q N − Q i ( s , a i ; θ ) ) 2 ] , {L_{i}}({\theta }) = {E_{s,a_{i},u_{i}(s,a_{i}),s'}}[{(y_{i}^{DQN} - Q_{i}(s,a_{i};{\theta }))^{2}}], Li(θ)=Es,ai,ui(s,ai),s′[(yiDQN−Qi(s,ai;θ))2],
上图里面红色的y为
y i D D Q N = u i ( s , a i ) + γ Q i ( s ′ , arg max a i ′ ∈ A i Q i ( s ′ , a i ′ ; θ ) ; θ − ) . y_{i}^{DDQN} = {u_{i}}(s,a_{i}) + \gamma Q_{i}\left ({s',\mathop {\arg \max }\limits _{a'_{i} \in {\mathcal{ A}}_{i}} Q_{i}(s',a'_{i};{\theta });\theta ^{-} }\right). yiDDQN=ui(s,ai)+γQi(s′,ai′∈AiargmaxQi(s′,ai′;θ);θ−).

应用案例:分布式动态下行链路波束成形
J. Ge, Y. -C. Liang, J. Joung and S. Sun, “Deep Reinforcement Learning for Distributed Dynamic MISO Downlink-Beamforming Coordination,” in IEEE Transactions on Communications, vol. 68, no. 10, pp. 6070-6085, Oct. 2020, doi: 10.1109/TCOMM.2020.3004524.
multi-cell MISO-IC model
a downlink cellular network of K cells
no intra-cell interference
all the BSs are equipped with a uniform linear array having N N N ( N ≥ 1 N≥1 N≥1) antenna elements.
max W ( t ) ∑ k = 1 K C k ( W ( t ) ) 8a s . t . 0 ≤ ∥ w k ( t ) ∥ 2 ≤ p m a x , ∀ k ∈ K , 8b \max _{\mathbf {W}{(t)}}~\sum _{k=1}^{K}C_{k}(\mathbf {W}{(t)}) \text{8a}\\{\mathrm{ s.t.}}~0\leq \left \|{\mathbf {w}_{k}{(t)}}\right \|^{2} \leq p_{\mathrm{ max}},~\forall k \in \mathcal {K},\text{8b} maxW(t) ∑k=1KCk(W(t))8as.t. 0≤∥wk(t)∥2≤pmax, ∀k∈K,8b
the beamformer of BS k k k
the available maximum transmit power budget of each BS
Limited-Information Exchange Protocol
a downlink data transmission framework
The first phase (phase 1) is a preparing phase for the subsequent data transmission
the second phase (phase 2) is for the downlink data transmission.
in the centralized approaches, the cascade procedure of collecting global CSI, computing beamformers, and sending beamformers to the corresponding BSs is supposed to be carried out within phase 1.
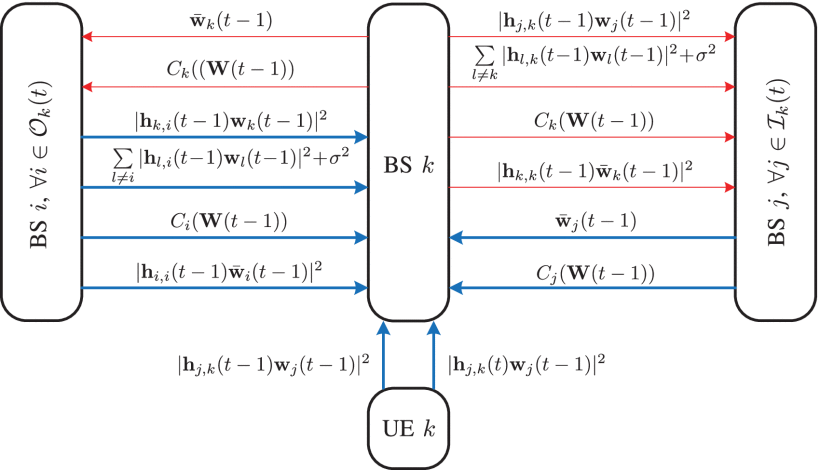
Designed limited-information exchange protocol in time slot t.
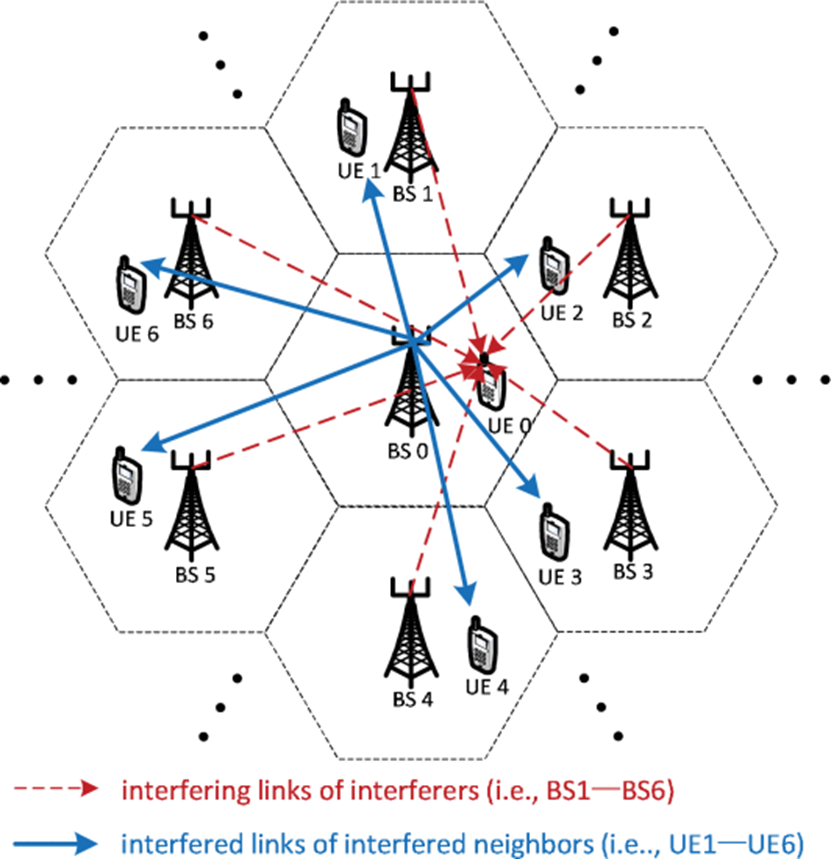
BSs are able to share their historical measurements and other information with their interferers and interfered neighbors.
- The received interference power from interferer j ∈ I k ( t ) j∈Ik(t) j∈Ik(t) in time slot t − 1 t−1 t−1
, i.e., ∣ ∣ h † j , k ( t − 1 ) w j ( t − 1 ) ∣ ∣ 2 ∣∣h†j,k(t−1)wj(t−1)∣∣2 ∣∣h†j,k(t−1)wj(t−1)∣∣2 . - The total interference-plus-noise power of UE k k k in time slot t − 1 t−1 t−1
, i.e., ∑ l ≠ k ∣ ∣ h † l , k ( t − 1 ) w l ( t − 1 ) ∣ ∣ 2 + σ 2 ∑l≠k∣∣h†l,k(t−1)wl(t−1)∣∣2+σ2 ∑l=k∣∣h†l,k(t−1)wl(t−1)∣∣2+σ2 . - The achievable rate of direct link k k k in time slot t − 1 t−1 t−1
, i.e., C k ( W ( t − 1 ) ) Ck(W(t−1)) Ck(W(t−1)) . - The equivalent channel gain of direct link k k k in time slot t − 1 t−1 t−1
, i.e., ∣ ∣ h † k , k ( t − 1 ) w ¯ k ( t − 1 ) ∣ ∣ 2 ∣∣h†k,k(t−1)w¯k(t−1)∣∣2 ∣∣h†k,k(t−1)w¯k(t−1)∣∣2 .
Distributed DRL-Based DTDE Scheme for DDBC
distributed-training-distributed-executing (DTDE)
distributed dynamic downlink-beamforming coordination (DDBC)
each BS is an independent agent
a multi-agent reinforcement learning problem
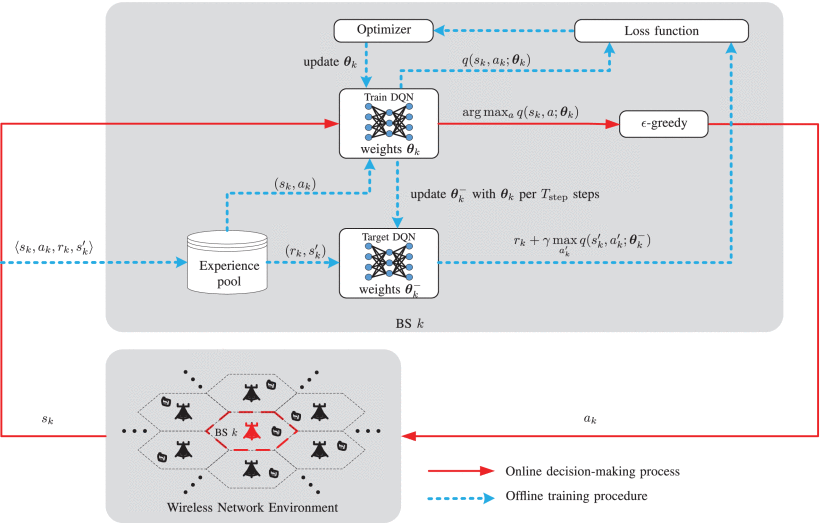
Illustration of the proposed distributed DRL-based DTDE scheme in the considered multi-agent system.
- Actions
A = { ( p , c ) , p ∈ P , c ∈ C } , \mathcal {A} = \{(p, {\mathbf{c}}),~p\in \mathcal {P},~{\mathbf{c}}\in \mathcal {C}\}, A={(p,c), p∈P, c∈C},
P = { 0 , 1 Q p o w − 1 p m a x , 2 Q p o w − 1 p m a x , ⋯ , p m a x } \mathcal {P}=\left \{{0, \tfrac {1}{Q_{\mathrm{ pow}}-1}p_{\mathrm{ max}},\,\,\tfrac {2}{Q_{\mathrm{ pow}}-1}p_{\mathrm{ max}},\,\,\cdots,\,\,p_{\mathrm{ max}}}\right \} P={0,Qpow−11pmax,Qpow−12pmax,⋯,pmax}
C = { c 0 , c 1 , ⋯ , c Q c o d e − 1 } \mathcal {C}=\left \{{\mathbf {c}_{0},\,\,\mathbf {c}_{1},\,\,\cdots,\,\,\mathbf {c}_{Q_{\mathrm{ code}}-1}}\right \} C={c0,c1,⋯,cQcode−1}
1.the transmit power of BS k in time slot t
2.code c k ( t ) ck(t) ck(t)
the total number of available actions is Q = Q p o w Q c o d e Q=QpowQcode Q=QpowQcode - States
1.Local Information
2.Interferers’ Information
3.Interfered Neighbors’ Information - Reward
the achievable rate of agent k k k
the penalty on BS k is defined as the sum of the achievable rate losses of the interfered neighbors j∈Ok(t+1) , which are interfered by BS k , as follows:
Distributed DRL-Based DTDE Scheme for DDBC

In training step t , the prediction error
L ( θ ) = 1 2 M b ∑ ⟨ s , a , r , s ′ ⟩ ∈ D ( r ′ − q ( s , a ; θ ) ) 2 L(\boldsymbol {\theta })= \frac {1}{2M_{b}}\sum \limits _{\langle s,a,r,s'\rangle \in \mathcal {D}}\left ({r'-q(s,a; \boldsymbol {\theta })}\right)^{2} L(θ)=2Mb1⟨s,a,r,s′⟩∈D∑(r′−q(s,a;θ))2
the target value of reward
r ′ = r + γ max a ′ q ( s ′ , a ′ ; θ − ) r'= r + \gamma \max \limits _{a'}q(s',a'; \boldsymbol {\theta }^{-}) r′=r+γa′maxq(s′,a′;θ−)
the optimizer returns a set of gradients shown in (22) to update the weights of the trained DQN through the back-propagation (BP) technique
∂ L ( θ ) ∂ θ = 1 M b ∑ ⟨ s , a , r , s ′ ⟩ ∈ D ( r ′ − q ( s , a ; θ ) ) ∇ q ( s , a ; θ ) . \frac {\partial L(\boldsymbol {\theta })}{\partial \boldsymbol {\theta }}= \frac {1}{M_{b}}\sum _{\langle s,a,r,s'\rangle \in \mathcal {D}}\left ({r'-q(s,a; \boldsymbol {\theta })}\right)\nabla q(s,a; \boldsymbol {\theta }). ∂θ∂L(θ)=Mb1∑⟨s,a,r,s′⟩∈D(r′−q(s,a;θ))∇q(s,a;θ).