递归算法学习——二叉树的伪回文路径-编程知识

递归算法学习——二叉树的伪回文路径

1，题目

给你一棵二叉树，每个节点的值为 1 到 9 。我们称二叉树中的一条路径是「伪回文」的，当它满足：路径经过的所有节点值的排列中，存在一个回文序列。

请你返回从根到叶子节点的所有路径中 伪回文 路径的数目。

示例 1：
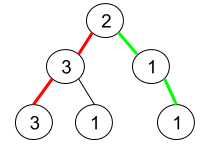
输入：root = [2,3,1,3,1,null,1]
输出：2 
解释：上图为给定的二叉树。总共有 3 条从根到叶子的路径：红色路径 [2,3,3] ，绿色路径 [2,1,1] 和路径 [2,3,1] 。在这些路径中，只有红色和绿色的路径是伪回文路径，因为红色路径 [2,3,3] 存在回文排列 [3,2,3] ，绿色路径 [2,1,1] 存在回文排列 [1,2,1] 。
示例 2：
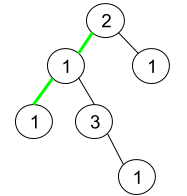
输入：root = [2,1,1,1,3,null,null,null,null,null,1]
输出：1 
解释：上图为给定二叉树。总共有 3 条从根到叶子的路径：绿色路径 [2,1,1] ，路径 [2,1,3,1] 和路径 [2,1] 。这些路径中只有绿色路径是伪回文路径，因为 [2,1,1] 存在回文排列 [1,2,1] 。
示例 3：
输入：root = [9]
输出：1
提示：

给定二叉树的节点数目在范围 [1, 105] 内
1 <= Node.val <= 9

2，题目接口

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/class Solution {public:int pseudoPalindromicPaths (TreeNode* root) {}};

3，解题思路及其代码

首先，这道题是一道二叉树的题目。看到二叉树首先便要先想到递归算法。刚好这道题也可以用递归来解决。解题思路如下：

1.因为是路径问题，所以我们要使用的便是递归算法里面的深度优先搜索：dfs。

2.根据题目意思，我们要做的便是统计各个数字出现的次数。如何统计呢？因为在这个题中的数据是1~9。所以我们可以开一个有10个空间大小的数组，然后以node->val为下标来统计个数。

在明确了这些关键点以后写出代码如下：
/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int count[10];//统计个数的数组int ans = 0;//统计伪回文数个数void dfs(TreeNode* root){if(root == nullptr){return;}count[root->val]++;if(root->right == nullptr&&root->left == nullptr)//一条路径结束后，开始统计这条路径上的每个出现的次数{int countsum = 0;for(int i = 0;i<10;i++){countsum+=count[i]%2;}if(countsum == 0||countsum==1)//当该条路径上的数字的出现次数都是偶数时，或者只有一个数出现奇数次。那这条路径便是伪回文数。{ans++;}}dfs(root->left);dfs(root->right);//回溯count[root->val]--;}int pseudoPalindromicPaths (TreeNode* root) {dfs(root);return ans;}
};