文章解读与仿真程序复现思路——电网技术EI\CSCD\北大核心《考虑系统一次频率响应特性的新型电力系统源网荷储协调鲁棒规划》-编程知识

这篇文章的标题涉及到新型电力系统的源（发电源）、网（电网）、荷（负荷，即用电需求）以及储（储能系统）的协调鲁棒规划，其中考虑了系统的一次频率响应特性。

让我们分解这个标题：

新型电力系统： 文章关注的是一种新型的电力系统，这可能意味着采用了新的技术、架构或策略来满足电力需求。
源网荷储协调： 文章讨论了发电源（源）、电网（网）、负荷（荷）以及储能系统（储）之间的协调。这可能包括优化发电源的运行、电网的管理、负荷的分配以及储能系统的调度，以实现系统整体的高效性和可靠性。
鲁棒规划： 鲁棒性是指系统对于不确定性和变化的适应能力。因此，鲁棒规划涉及到在面对各种不确定性和变化时，系统能够保持高效运行的策略和方法。
考虑系统一次频率响应特性： 文章在协调规划中考虑了系统的一次频率响应特性。一次频率响应通常与系统惯性、发电机的动力学特性以及负荷的瞬时变化等相关。这表明文章不仅关注系统的静态性能，还考虑了系统在瞬时或频率响应方面的特性。

综合起来，这篇文章的核心内容可能是关于如何通过一种新型电力系统的协调规划，在考虑系统的一次频率响应特性的同时，提高系统的鲁棒性，以更有效地满足电力需求并应对各种不确定性和变化。

摘要：新能源在电力系统中占比逐步提升，且新能源的不确定性给系统安全稳定运行带来挑战，并且构建源网荷储协调发展的灵活电力平衡体系是新型电力系统的重要内核。为此，提出考虑系统一次频率响应特性的新型电力系统源网荷储协调鲁棒规划模型。首先，提出以最小化设备投建成本、运行成本和电量不平衡惩罚成本的和为目标函数；其次，考虑需求响应和储能来缓解风光电站的出力波动，建立需求响应和储能装置的运行约束，形成电力系统源网荷储协调规划模型；进一步采用鲁棒优化方法处理风光出力的不确定性，并对系统一次频率响应特性进行建模，结合频率变化率和频率最低点等频率稳定相关约束，来初步保证不确定场景下系统运行的频率稳定，将模型转化为混合整数线性规划问题，并通过列约束生成法(column-and-constraint generation method,CCG)进行求解；最后，通过算例分析验证所提鲁棒规划方法的有效性。

这段摘要讨论了新能源在电力系统中所占比例逐步增加，新能源的不确定性给系统的安全稳定运行带来挑战，并提出了解决这些挑战的方法和技术。

新能源增加和不确定性挑战： 摘要指出新能源在电力系统中所占比例逐步提高，这可能指的是可再生能源（如风能、太阳能等）在总发电量中所占的比例正在增加。然而，这些可再生能源的波动性和不确定性会给电力系统的安全稳定运行带来挑战，因为其输出受天气和其他环境因素的影响而变化不确定。
构建灵活电力平衡体系的重要性： 文中指出，构建源（发电源）、网（电网）、荷（负荷）、储（储能系统）之间协调发展的灵活电力平衡体系是新型电力系统的重要内核。这意味着需要一种能够协调管理不同能源供应、电力需求和储能系统的方法，以确保系统运行平稳、高效、可靠。
提出的解决方案： 为了应对这些挑战，摘要提出了一种新型的电力系统规划模型。这个模型首先将最小化设备投建成本、运行成本和电量不平衡惩罚成本的总和作为目标函数。其次，考虑了需求响应和储能系统，用以平衡风光电站等可再生能源的出力波动，并建立了相应的运行约束。此外，采用了鲁棒优化方法来处理风光能源出力的不确定性，并对系统的一次频率响应特性进行了建模，以确保在不确定情景下系统频率的稳定。这将模型转化为混合整数线性规划问题，并采用列约束生成法来求解这个问题。
验证方法有效性： 最后，通过算例分析验证了提出的鲁棒规划方法的有效性，这意味着这种方法在一定程度上能够解决电力系统面临的不确定性和稳定性问题。

总体来说，这段摘要描述了新能源增加对电力系统带来的挑战，以及提出的一种新型电力系统规划模型，该模型旨在应对新能源不确定性、实现源网荷储协调，并通过鲁棒规划方法确保系统的稳定运行。

关键词:新型电力系统源网荷廬鲁棒规址-次频率响应新能源

这些关键词涵盖了电力系统中一些重要的概念和技术方面：

新型电力系统： 指的是基于新技术、新能源以及新型能源管理和分配方法构建的电力系统。这种系统可能包括更多的可再生能源、智能化的网格管理、更高效的能源储存和供应管理等方面的创新。
源网荷储协调： 涉及到电力系统中的四个主要部分：源（发电源）、网（电网）、荷（负荷，即能源消耗者）、储（储能系统）。协调这些要素之间的关系，以实现电力系统的平衡、高效和可靠运行。
鲁棒规划： 指的是在面对不确定性或变化时仍能保持稳定性和高效性的规划方法。在电力系统中，这可能意味着考虑到新能源不确定性（如风能或太阳能的波动性），制定能够应对这种不确定性的系统规划方案。
一次频率响应： 指的是电力系统对于频率变化的响应速度和能力。电力系统的频率是其稳定运行的关键指标之一，一次频率响应能力强表示系统能够快速调整以维持稳定的频率。
新能源： 指的是相对传统化石能源而言的新型能源，例如风能、太阳能、水能等可再生能源，它们通常具有环保、可再生等特点，但也可能具有波动性和不确定性。

这些关键词的整合可能指向针对新型电力系统中新能源不确定性的挑战，提出了鲁棒规划方法来协调源、网、荷、储之间的关系，尤其关注了一次频率响应方面，以确保电力系统在新能源波动性影响下的稳定性和可靠性。

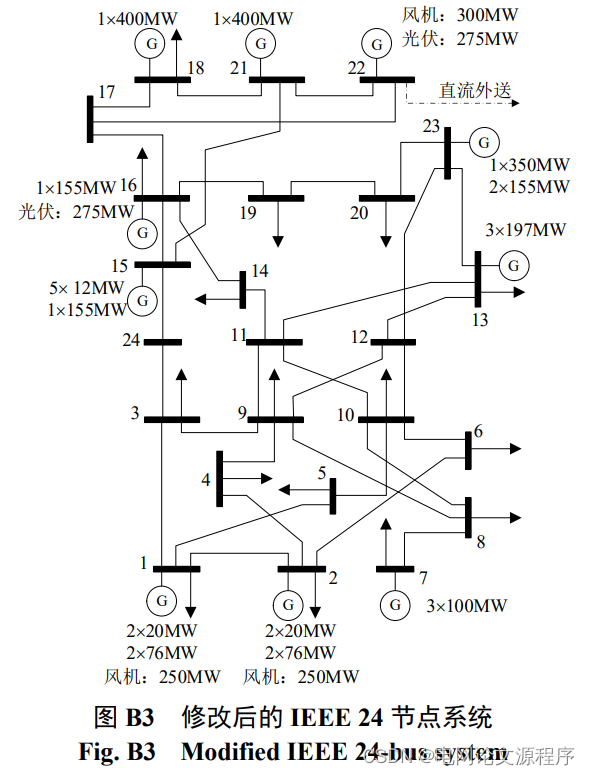
仿真算例：本文算例选用修改后的 IEEE 24 节点系统[33]对提出的源网荷储协调鲁棒规划模型进行验证和分析。修改后的 IEEE 24 节点系统包括 38 条已有线路、26 台已有火电机组、17 个电力负荷、3 座风电场和 2 个光伏电站，具体结构见附录 B 中图 B3。风电场分别接在节点 1、2、22 上，光伏电站分别接在节点 16、22 上。直流联络线送端连接节点 22。另外，还考虑 18 台候选火电机组、16 条候选线路和 17 组候选需求响应装置、6 个候选储能装置。设定规划扩建周期为 5 年，第一年的电力负荷，风力发电和光伏发电最大值分别为 2850、800 和550MW，每年的增长率分别为 3%、8%和 9%。设置直流外送功率最小值和最大值分别为 100MW 和500MW，日输送功率达到 6000MWh。电力系统的有功负荷和风电场、光伏电站在第一年典型日内预测功率变化曲线见录 B 中图 B4。负荷不平衡的成本系数设置为 106 元/MWh，弃风、弃光的惩罚成本系数设置为 1000 元/MWh。贴现率设置为 0.05。违反安全规定最大值设定为0.01MWh。

仿真程序复现思路：

首先，根据文章描述，仿真选用了修改后的 IEEE 24 节点系统进行验证和分析。这个系统包括了已有线路、火电机组、电力负荷、风电场、光伏电站以及其他候选元素。为了更详细地说明仿真程序的编程部分，我们可以采用一种伪代码的方式，表示主要的仿真步骤和计算过程。

# 导入必要的库
import numpy as np
import pandas as pd
from scipy.optimize import minimize# 定义系统参数
nodes = 24
existing_lines = 38
existing_generators = 26
existing_loads = 17
wind_farms = 3
solar_farms = 2
existing_line_capacity = np.array(...)  # 定义已有线路的容量
existing_generator_capacity = np.array(...)  # 定义已有火电机组的容量
existing_load_demand = np.array(...)  # 定义已有电力负荷需求
wind_capacity = np.array(...)  # 定义风电场容量
solar_capacity = np.array(...)  # 定义光伏电站容量
dc_line_capacity = np.array(...)  # 定义直流联络线容量
candidate_generators = 18
candidate_lines = 16
candidate_demand_response_units = 17
candidate_energy_storage_units = 6
planning_period = 5
load_growth_rate = 0.03
wind_growth_rate = 0.08
solar_growth_rate = 0.09
dc_min_power = 100
dc_max_power = 500
dc_max_daily_energy = 6000# 定义仿真参数
simulation_years = 5
discount_rate = 0.05
imbalance_cost_coefficient = 106
penalty_cost_coefficient = 1000
max_violation = 0.01# 生成负荷和可再生能源的时间序列数据（示例数据，具体数据根据实际需求生成）
load_profile = generate_load_profile(...)
wind_power_profile = generate_renewable_profile(...)
solar_power_profile = generate_renewable_profile(...)# 定义优化问题的目标函数
def objective_function(x):# x 是优化变量，表示各种扩建和调度决策# 在这里编写目标函数的计算过程...# 定义优化问题的约束条件
constraints = ({'type': 'eq', 'fun': constraint_function1},{'type': 'eq', 'fun': constraint_function2},# 添加其他约束条件)# 执行优化
initial_guess = np.zeros(...)  # 初始猜测
result = minimize(objective_function, initial_guess, constraints=constraints)# 输出结果
print("Optimal solution:")
print(result.x)# 在这里可以根据仿真结果进行进一步的分析和可视化
...

上述代码只是一个简化的伪代码示例，实际情况中需要根据具体问题和数据结构进行更详细和精确的编程。在实际实现中，可能需要使用专业的数学优化库（如SciPy）来求解优化问题，同时需要注意处理不同元素之间的耦合关系和约束条件。具体的仿真程序的编写需要根据具体的问题和数据结构进行更详细的设计。