目录

全排列问题

leetcode46题.全排列

leetcode47题.全排列II

---

对回溯算法感兴趣的朋友也可以多多支持一下我的其他文章。

回溯算法详解-CSDN博客

经典的回溯算法题leetcode组合问题整理及思路代码详解-CSDN博客

经典的回溯算法题leetcode子集问题思路代码详解-CSDN博客

全排列问题

组合问题、子集问题和全排列问题是类似的，但是这三种问题的理解与学习可以说是递进的，你先弄懂前面两种问题，全排列问题就更好懂一些。无论这三种哪个问题，我们都会把它们画成一棵树来看。类似下图：

 在我们的子集和组合问题中，我们的选择是从左到右的选，比如在一个{1，2，3}的集合中，我们按照1、2、3的顺序依次选，选到3的时候就没办法再往下选了，但全排列问题是可以继续选下去的，这就是一个很大的不同点，如下图所示：

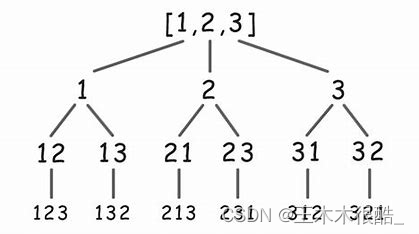
在组合问题和子集问题中我们用index来遍历获得需要的集合，但全排列问题就需要一个数组visit()用来标记是否被标记过。

leetcode46题.全排列

46. 全排列 - 力扣（LeetCode）

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以按任意顺序返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

class Solution {//储存结果集List<List<Integer>> res = new ArrayList<>();//保存临时存放的结果List<Integer> temp = new ArrayList<>();public List<List<Integer>> permute(int[] nums) {// 记录那些被访问过的元素boolean[] visited = new  boolean[nums.length];backTrack(nums, visited);return res;}//回溯函数void backTrack(int[] nums, boolean[] visited){// 结束条件if(temp.size() == nums.length){res.add(new ArrayList<>(temp));return;}for(int i = 0; i < nums.length; i++){// 判断以前是否被访问过if(visited[i] == true){continue;}// 开始处理visited[i] = true;temp.add(nums[i]);backTrack(nums, visited);// 撤销之前的操作visited[i] = false;temp.remove(temp.size() - 1);}}
}

leetcode47题.全排列II

47. 全排列 II - 力扣（LeetCode）

给定一个可包含重复数字的序列 nums ，按任意顺序返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]
输出：
[[1,1,2],[1,2,1],[2,1,1]]

示例 2：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

class Solution {List<List<Integer>> res = new ArrayList<>();List<Integer> temp = new ArrayList<>();public List<List<Integer>> permuteUnique(int[] nums) {Arrays.sort(nums);// 记录那些被访问过的元素boolean[] visited = new  boolean[nums.length];backTrack(nums, visited);return res;}void backTrack(int[] nums, boolean[] visited){// 结束条件if(temp.size() == nums.length){res.add(new ArrayList<>(temp));return;}for(int i = 0; i < nums.length; i++){// 去掉重复if(i > 0 && nums[i] == nums[i-1] && visited[i-1] == false){continue;}// 判断以前是否被访问过if(visited[i] == true){continue;}// 开始处理visited[i] = true;temp.add(nums[i]);backTrack(nums, visited);// 撤销之前的操作visited[i] = false;temp.remove(temp.size() - 1);}}
}