超详细！|优化算法性能测试标准及代码实现-编程知识

在这里插入图片描述

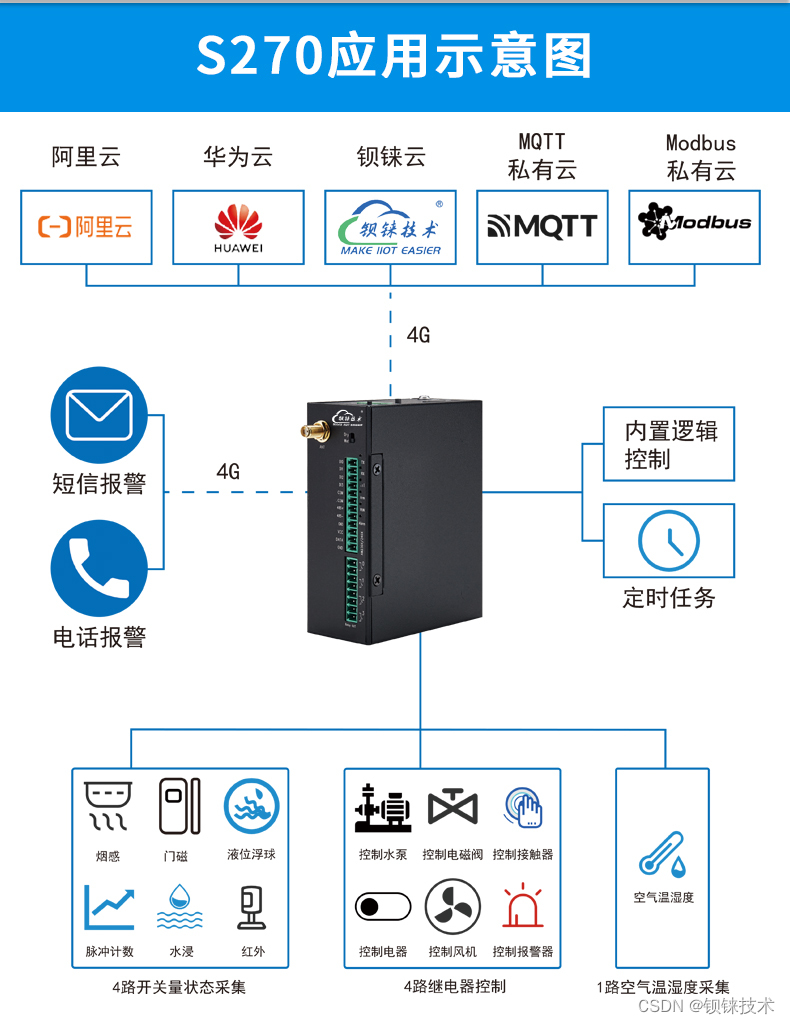
由于有许多同学对我之前所用的优化算法测试函数的来源及其内容并不清楚，这里作者就给大家整理了5大常用的CEC测试函数集相关内容及其代码实现，当然作者能力有限，若有不当之处也希望与各位一起讨论交流，一起进步。

以上

处理优化问题时，研究单目标优化算法是研究多目标优化算法、约束优化算法等更复杂优化算法的基础。近年来，为了解决优化问题，人们提出许多新型优化算法，进化计算大会因此举办多场关于单目标实参优化竞赛。

IEEE 国际进化计算大会（IEEE Congress on Evolutionary Computation，IEEE CEC）是进化计算领域中最大和最重要的会议之一，为了公平评估算法寻优性能，在优化竞赛中提出了单目标实参数数值优化竞赛的问题定义和评估标准。所有新型进化算法和基于群体的算法都统一对单目标基准问题进行测试。

鉴于最大化与最小化问题可以进行转换，大会定义所有测试函数都是最小化问题，即：Min f(x), 其中，x 为 D 维空间变量，f(x)代表目标函数。

下面作者将介绍CEC2017、CEC2019、CEC2020、CEC2022这几个测试函数集。而CEC2005测试函数集在作者前面的文章中有过介绍，这里不再赘述。

00 目录

1 各CEC测试函数集介绍

2 源码获取

01 各CEC测试函数集介绍

这些测试函数集有四种类型的函数：单峰、多峰、混合和组合函数。单峰函数只有一个最优解，这是用来衡量算法的收敛速度和寻优能力。另外三种情况都有多个最优解，利用这些最优解来测试算法的局部最优逃逸能力和勘探能力等。

1.1 CEC2017

CEC2017测试函数集[1]的使用相当广泛，它对算法有一定挑战性且学术上认可度较高。测试集所有函数都进行了旋转和位移，增加了算法寻优难度。函数主要包含29个测试函数：

其中F1、F3为没有局部最小只有全局最小的单峰函数，这些单峰函数能检验算法的收敛能力；F4-F10为具有局部极值点的多峰函数，这些多峰函数用于测试算法跳出局部最优的能力；F11-F20是经旋转/位移后包含三个或以上的CEC2017基准函数的混合函数，每个子函数被赋予一定权重；F21-F30是由至少三个混合函数或CEC 2017基准函数旋转移位后组成的复合函数，每个子函数有额外偏置值和一个权重，这些组合函数进一步增加了算法的优化难度。（其中原函数集的F2函数被官方删除了，原因是F2不稳定）

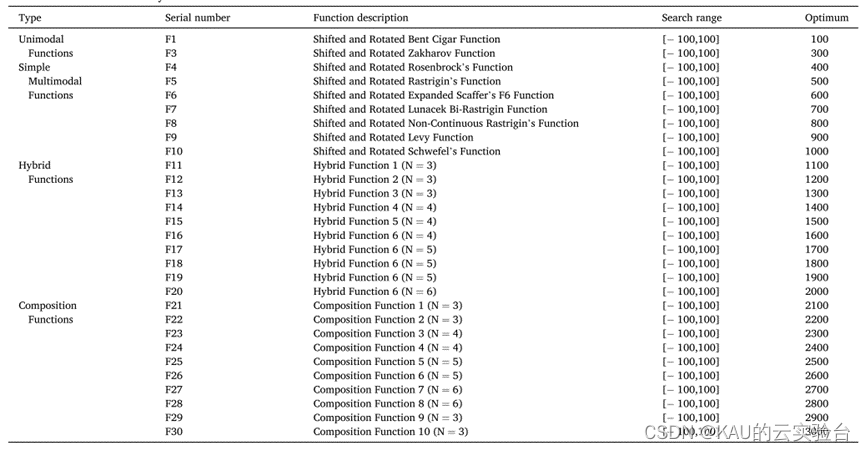
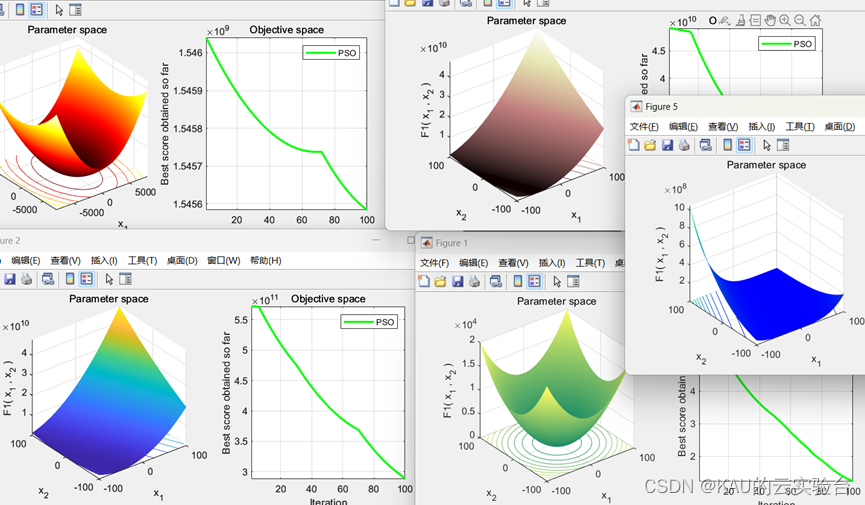
表中展示了CEC2017的函数名称、变量范围、最优值在这里插入图片描述

部分函数图像：
在这里插入图片描述

1.2 CEC2019

CEC2019函数集[2]是对元启发式算法的性能进行测试的相当有效的基准函数。在CEC 2019中，F1-F3函数具有不同的维度值和范围，F4-F10函数是10维最小化问题。由于CEC2019测试函数许多都是多峰函数，因此非常具有挑战性。

在这里插入图片描述

部分函数图像：

在这里插入图片描述

1.3 CEC2020

CEC2020函数集[3]由十个相当困难的优化问题组成，它由一个组合的单峰函数F1，三个经过旋转和位移的多峰函数F2-F4，三个混合函数F5-F7，三个复合函数F8-F10组成。每个优化函数都可在多个维度上定义。
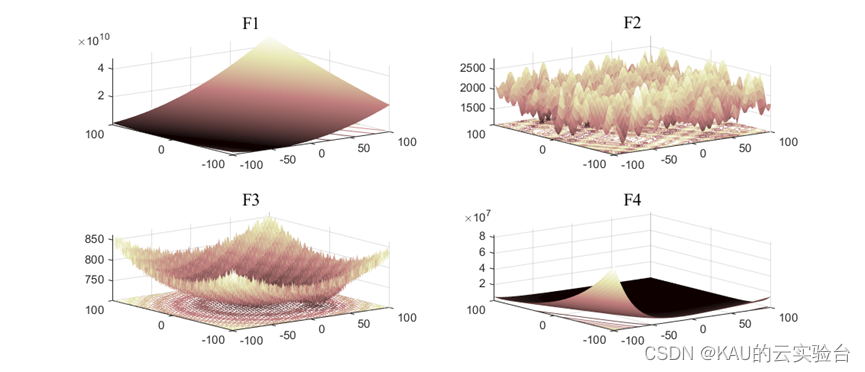
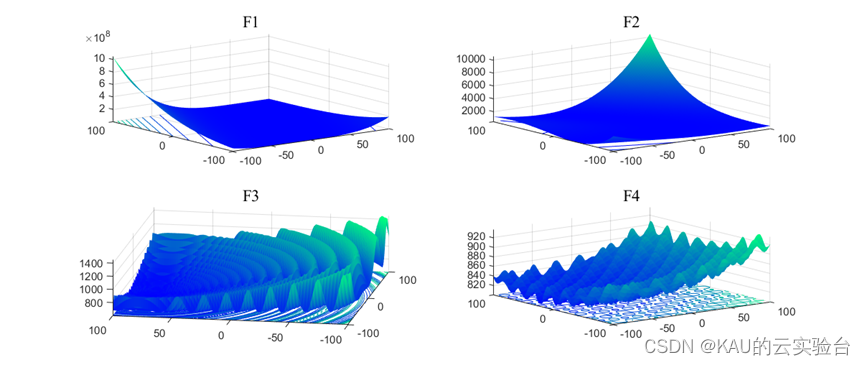
在这里插入图片描述

部分函数图像：
在这里插入图片描述

1.4 CEC2022

CEC2022[4]是评价算法性能和验证其求解复杂OP能力的有效方法。它由12个基准函数组成，包括单峰、多峰、混合和复合函数，其中F1是单峰函数，F2-F5是多峰函数，F6-F8是混合函数，其可以是单峰或多峰，F9-F12是复合且多模态的函数。
在这里插入图片描述

部分函数图像：
在这里插入图片描述

1.5 测试函数集的使用

了解了这些基本的测试函数集后，我们还必须知道如何使用测试函数集以合理验证算法性能。通常，可以将改进的算法与一些传统算法(如GA、PSO、GWO、SSA、SMA等)对比，在这些测试函数上运行以检验算法各方面(收敛能力、跳出局部最优能力等)性能，同时为了避免偶然因素的影响，通常会将算法独立运行N次，取一些性能参数如标准差std、平均值mean、最优/差值等使结果具有统计学的意义，进而对比算法性能，通过这些方法即可在一定程度上验证算法的优越性。

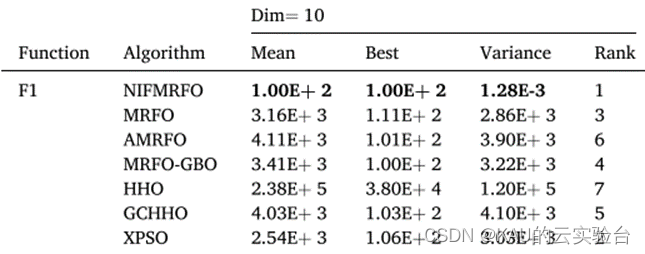
如：图片来源文献，文献中列出了均值、最优值、方差，然后根据结果进行排序

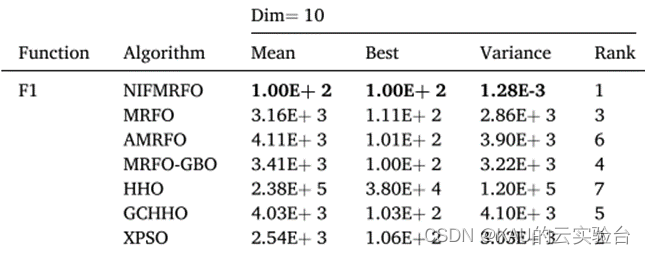
在这里插入图片描述

来源：An efficient manta ray foraging optimization algorithm with individual information interaction and fractional derivative mutation for solving complex function extremum and engineering design problems

02源码获取

作者整理了CEC2005、CEC2017、CEC2019、CEC2020、CEC2022的函数调用/绘图的一键实现，代码中以PSO算法为例进行计算。
在这里插入图片描述

其中example_pso.m是主程序，一键运行即可
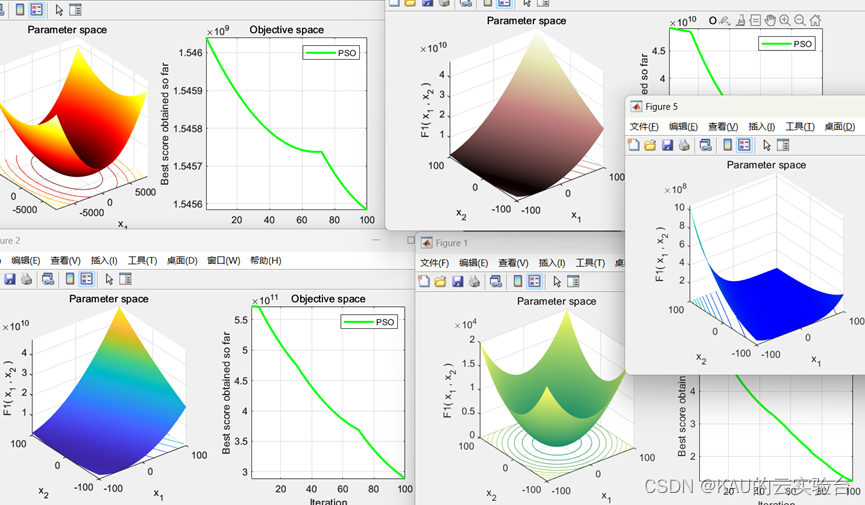
在这里插入图片描述

以F1函数为例，运行结果：
在这里插入图片描述

代码获取方式：

在GZH(KAU的云实验台)后台回复：CEC

本文介绍了常用的一些测试函数集及其使用，可以收藏本文作为一个参考工具以便需要时查阅，更多干货可以关注作者不迷路！

参考文献

[1] Wu, G., Mallipeddi, R., & Suganthan, P. N. (2017). Problem definitions and evaluation criteria for the CEC 2017 competition on constrained real-parameter optimization.National University of Defense Technology, Changsha, Hunan, PR China and Kyungpook National University, Daegu, South Korea and Nanyang Technological

University, Singapore, Technical Report.

[2] K. Price, N. Awad, M. Ali, P. Suganthan, Problem definitions and evaluation criteria for the 100-digit challenge special session and competition on single objective numerical optimization, Technical Report, Nanyang Technological University Singapore, 2018.

[3] C. Yue, K. Price, P.N. Suganthan, J. Liang, M.Z. Ali, B. Qu, N.H. Awad,P.P. Biswas, Problem Definitions and Evaluation Criteria for the CEC 2020 Special Session and Competition on Single Objective Bound Constrained Numerical Optimization, Tech. Rep 201911, Comput. Intell. Lab., Zhengzhou Univ., Zhengzhou, China, 2019.

[4] D. Yazdani, J. Branke, M.N. Omidvar, X.D. Li, C.H. Li, M. Mavrovouniotis, T.T. Nguyen, S.X. Yang, X. Yao, IEEE CEC 2022 competition on dynamic optimization problems generated by generalized moving peaks benchmark, (2021).

另：如果有伙伴有待解决的优化问题（各种领域都可），可以发我，我会选择性的更新利用优化算法解决这些问题的文章。

如果这篇文章对你有帮助或启发，可以点击右下角的赞/在看(ง •̀_•́)ง(不点也行)，你们的鼓励就是我坚持的动力！