python：傅里叶分析，傅里叶变换 FFT-编程知识

使用python进行傅里叶分析，傅里叶变换 FFT 的一些关键概念的引入：

1.1.离散傅里叶变换（DFT）
离散傅里叶变换(discrete Fourier transform) 傅里叶分析方法是信号分析的最基本方法，傅里叶变换是傅里叶分析的核心，经过它把信号从时间域变换到频率域，进而研究信号的频谱结构和变化规律。可是它的致命缺点是：计算量太大，时间复杂度过高，当采样点数过高的时候，计算缓慢，由此出现了DFT的快速实现，即下面的快速傅里叶变换FFT。
1.2.快速傅里叶变换（FFT）
计算量更小的离散傅里叶的一种实现方法。快速傅氏变换（FFT），是离散傅氏变换的快速算法，它是根据离散傅氏变换的奇、偶、虚、实等特性，对离散傅立叶变换的算法进行改进获得的。
1.3.采样频率以及采样定率
采样频率，也称为采样速度或者采样率，定义了每秒从连续信号中提取并组成离散信号的采样个数，它用赫兹（Hz）来表示。采样频率的倒数是采样周期或者叫做采样时间，它是采样之间的时间间隔。通俗的讲采样频率是指计算机每秒钟采集多少个信号样本。

采样定理，又称香农采样定理，奈奎斯特采样定理，是信息论，特别是通信与信号处理学科中的一个重要基本结论。采样定理指出，若是信号是带限的，而且采样频率高于信号带宽的两倍，那么，原来的连续信号能够从采样样本中彻底重建出来。

1.4.如何理解采样定理
在对连续信号进行离散化的过程当中，不免会损失不少信息，就拿一个简单地正弦波而言，若是我1秒内就选择一个点，很显然，损失的信号太多了，光着一个点我根本不知道这个正弦信号究竟是什么样子的，天然也没有办法根据这一个采样点进行正弦波的还原，很明显，我采样的点越密集，那越接近原来的正弦波原始的样子，天然损失的信息越少，越方便还原正弦波。

采样定理说明采样频率与信号频率之间的关系，是连续信号离散化的基本依据。它为采样率创建了一个足够的条件，该采样率容许离散采样序列从有限带宽的连续时间信号中捕获全部信息。
编写 test_fft_1.py 如下

# -*- coding: utf-8 -*-
""" 使用scipy包实现快速傅里叶变换 """
import numpy as np
from scipy.fftpack import fft, ifft
import matplotlib.pyplot as plt
from matplotlib.pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] #显示中文
mpl.rcParams['axes.unicode_minus'] = False   #显示负号# 采样点选择1400个，由于设置的信号频率份量最高为600赫兹，根据采样定理知采样频率要大于信号频率2倍，
# 因此这里设置采样频率为1400赫兹（即一秒内有1400个采样点，同样意思的）
x = np.linspace(0,1,1400)
#设置须要采样的信号，频率份量有200，400和600
y = 7*np.sin(2*np.pi*200*x) + 5*np.sin(2*np.pi*400*x) + 3*np.sin(2*np.pi*600*x)
fft_y = fft(y) #快速傅里叶变换
N= 1400
x = np.arange(N) # 频率个数
half_x = x[range(int(N/2))] #取一半区间
abs_y = np.abs(fft_y) # 取复数的绝对值，即复数的模(双边频谱)
angle_y = np.angle(fft_y) #取复数的角度
normalization_y = abs_y/N #归一化处理（双边频谱）
normalization_half_y = normalization_y[range(int(N/2))] #因为对称性，只取一半区间（单边频谱）
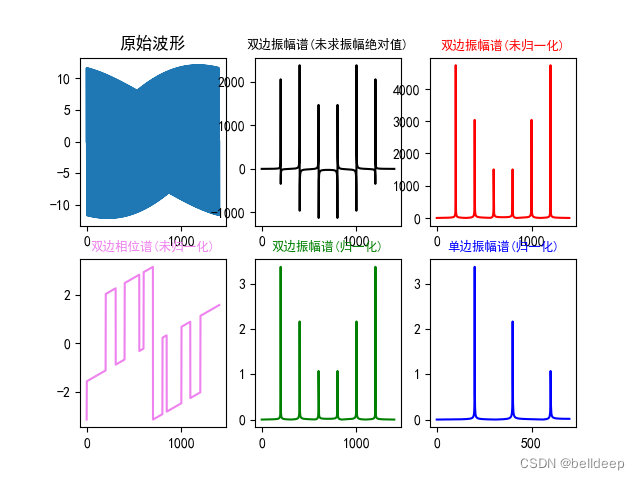
plt.subplot(231)
plt.plot(x,y) 
plt.title('原始波形')
plt.subplot(232)
plt.plot(x,fft_y,'black')
plt.title('双边振幅谱(未求振幅绝对值)',fontsize=9,color='black')
plt.subplot(233)
plt.plot(x,abs_y,'r')
plt.title('双边振幅谱(未归一化)',fontsize=9,color='red')
plt.subplot(234)
plt.plot(x,angle_y,'violet')
plt.title('双边相位谱(未归一化)',fontsize=9,color='violet')
plt.subplot(235)
plt.plot(x,normalization_y,'g')
plt.title('双边振幅谱(归一化)',fontsize=9,color='green')
plt.subplot(236)
plt.plot(half_x,normalization_half_y,'blue')
plt.title('单边振幅谱(归一化)',fontsize=9,color='blue')
plt.show()

运行 python test_fft_1.py

傅里叶定理指出，任何频率为f0的周期信号都可以通过将频率为f0,2f0,3f0,4f0,5f0等的“正弦波”（正弦波）相加而精确地构建。将周期时域信号分割为正弦波称为傅里叶分析。
“傅里叶级数”中的每个正弦曲线的特征在于频率振幅，以及阶段f0被称为基频。
2f0、3f0、4f0等被称为谐波。

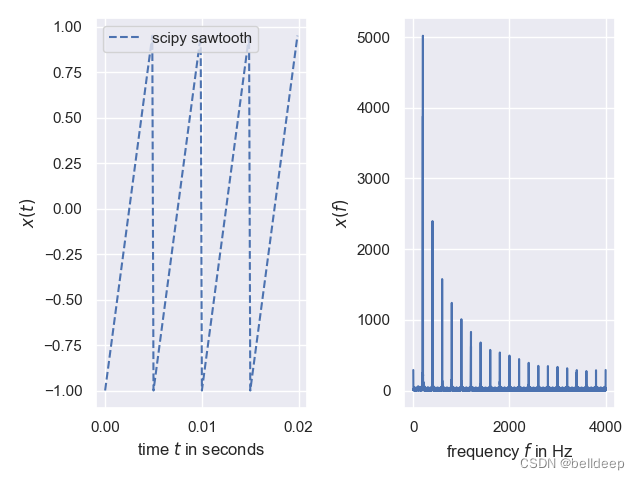
编写 test_sawtooth.py 如下

# -*- coding: utf-8 -*-
"""使用scipy中的 sawtooth()生成了频率为f=200Hz的锯齿信号，持续时间为2秒。"""
import matplotlib.pyplot as plt  # plotting
import seaborn as sns            # styling (uncomment if you want)
import numpy as np
from scipy import signal as sig     # for easy sawtooth signal generationsns.set()
fs=8000                   # sampling frequency
t = np.arange(0, 2, 1/fs) # time vector
f = 200                   # frequency in Hz for scipy sawtooth
saw_tooth = sig.sawtooth(2 * np.pi * f * t)
# plot first 20 ms (=160 samples at sampling frequency of 8000 Hz)
plt.subplot(1,2,1)
plt.plot(t[0:160], saw_tooth[0:160], '--', label='scipy sawtooth')
plt.xlabel('time $t$ in seconds')
plt.ylabel('$x(t)$')
plt.legend()# calculate the spectum (frequency domain representation)
FFT_length = 2**15 # take a power of two which is larger than the signal length
f = np.linspace(0, fs/2, num=int(FFT_length/2+1))
spectrum = np.abs(np.fft.rfft(saw_tooth, n=FFT_length))
# plot the spectrum
plt.subplot(1,2,2)
plt.plot(f,spectrum)
plt.xlabel('frequency $f$ in Hz')
plt.ylabel('$x(f)$')
plt.tight_layout() # this allowes for some space for the title text.
plt.show()

运行 pytho test_sawtooth.py