1 .矩阵乘法满足结合律,但不满足交换律。
如下图中,UWQ三个矩阵,(UW)Q 和U(WQ)的2种结合,证明矩阵乘法满足结合律。

AB 和BA的表达式,如下图中,相同的条件是对应的4项相同(两个对称矩阵必然满足条件),否则两者的值必然不同:

- 对称矩阵A(也可以不是对称矩阵)求对角阵或特征值。正数的特征值的个数就是正惯性指数,负数的特征值个数就是负惯性指数。实对称矩阵的特征值必然是实数,特征向量必然线性无关且正交,即AQ=QLamda,其中Lamda是以A的特征值为迹的对角矩阵,即A= QBQ^(-1)(Q ^(-1)为Q的逆矩阵),此定理称为“谱定理”。
对称矩阵一定可以写成:B= (A^t) * (A),即对称矩阵来源于矩阵和它的转置矩阵的乘积。
- 正定矩阵中“正定”的含义:对于任意向量x, (x ^ t)* A*x >0。
该性质的证明思路:
(1) 正定矩阵的二次型的可以化为标准型,所以二次型的值必然大于0。
(2) (x ^t)(B ^ t)(Lamda)(B)(x) > 0,其中Lamda是以A的特征值为迹的对角矩阵,有转置矩阵的性质得知其值必然大于0。
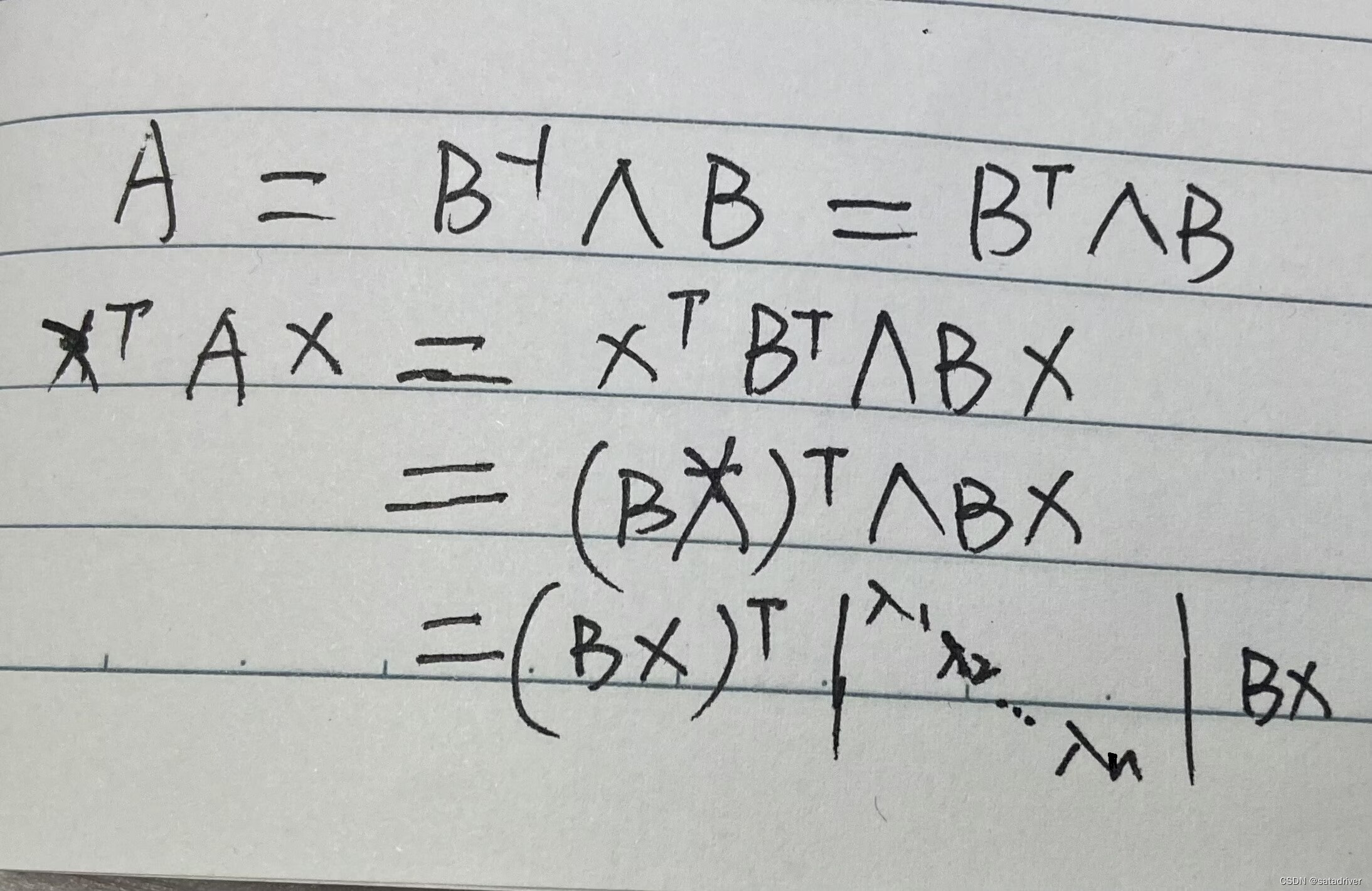
(3) 其他方法也可得证。
- 合同:就是两个矩阵有相同的正负惯性指数。在实数域上,只要两个矩阵的正负惯性指数相同,即可以认为两个矩阵存在合同。这是非常重要的判别的一句话!