线性模型是一类用于建模输入特征与输出之间线性关系的统计模型。这类模型的基本形式可以表示为:
其中:
是模型的输出(目标变量)。
是截距(常数项,表示在所有输入特征都为零时的输出值)。
是权重,表示每个特征对输出的影响程度。
是输入特征。
线性模型的任务是学习适当的权重 ,以最好地拟合训练数据,并对未见过的数据做出准确的预测。线性模型在不同领域中有广泛的应用,包括回归问题和分类问题。
线性模型的训练通常涉及到一个优化问题,目标是最小化损失函数。损失函数可以是均方误差(对于回归问题)或交叉熵等(对于分类问题)。优化算法(例如梯度下降)被用于调整权重,使得损失函数达到最小值。
不同类型的线性模型包括:
1. 线性回归(Linear Regression): 用于连续目标变量的预测。
2. 逻辑回归(Logistic Regression):用于二分类问题,输出是概率值。
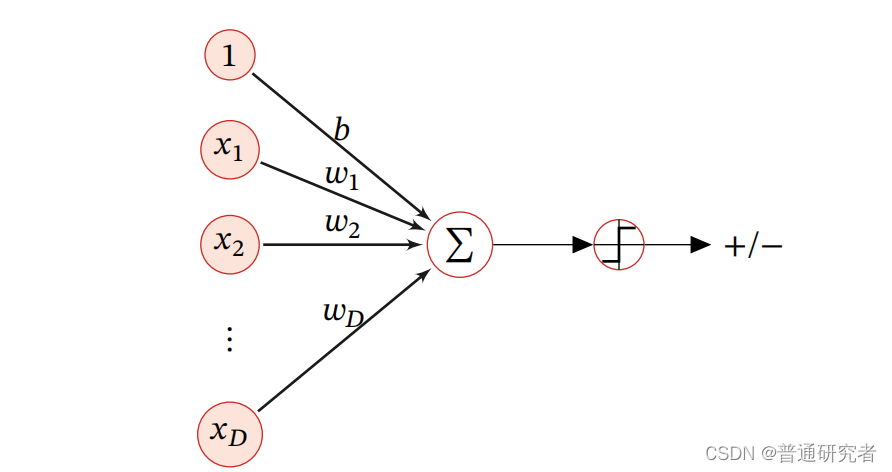
(1) 二分类的线性模型
3. 多项式回归(Polynomial Regression): 扩展线性回归,允许特征的多项式组合。
4. 岭回归(Ridge Regression)和Lasso回归(Lasso Regression): 用于处理特征共线性和过拟合。
5. 支持向量机(Support Vector Machines,SVM): 可用于线性和非线性分类问题。
线性模型的优势在于简单且易于解释,但对于复杂的非线性关系可能表现不佳。在实际应用中,特别是在深度学习等领域的崛起后,线性模型通常被更复杂的模型取代。
示例代码:
# 导入必要的库
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt# 生成示例数据
np.random.seed(42)
# 生成包含随机噪声的输入特征 X 和目标输出 y
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)# 划分数据集
# 将数据集划分为训练集和测试集,80% 用于训练,20% 用于测试
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建并训练线性回归模型
# 创建线性回归模型的实例
model = LinearRegression()
# 使用训练数据对模型进行训练
model.fit(X_train, y_train)# 在测试集上进行预测
# 使用训练好的模型对测试集进行预测
y_pred = model.predict(X_test)# 评估模型性能
# 计算预测值与真实值之间的均方误差
mse = mean_squared_error(y_test, y_pred)
print(f'Mean Squared Error: {mse}')# 可视化结果
# 绘制散点图表示真实值,并绘制回归线表示模型的预测
plt.scatter(X_test, y_test, color='black')
plt.plot(X_test, y_pred, color='blue', linewidth=3)
plt.xlabel('X')
plt.ylabel('y')
plt.title('Linear Regression Example')
plt.show()结果:
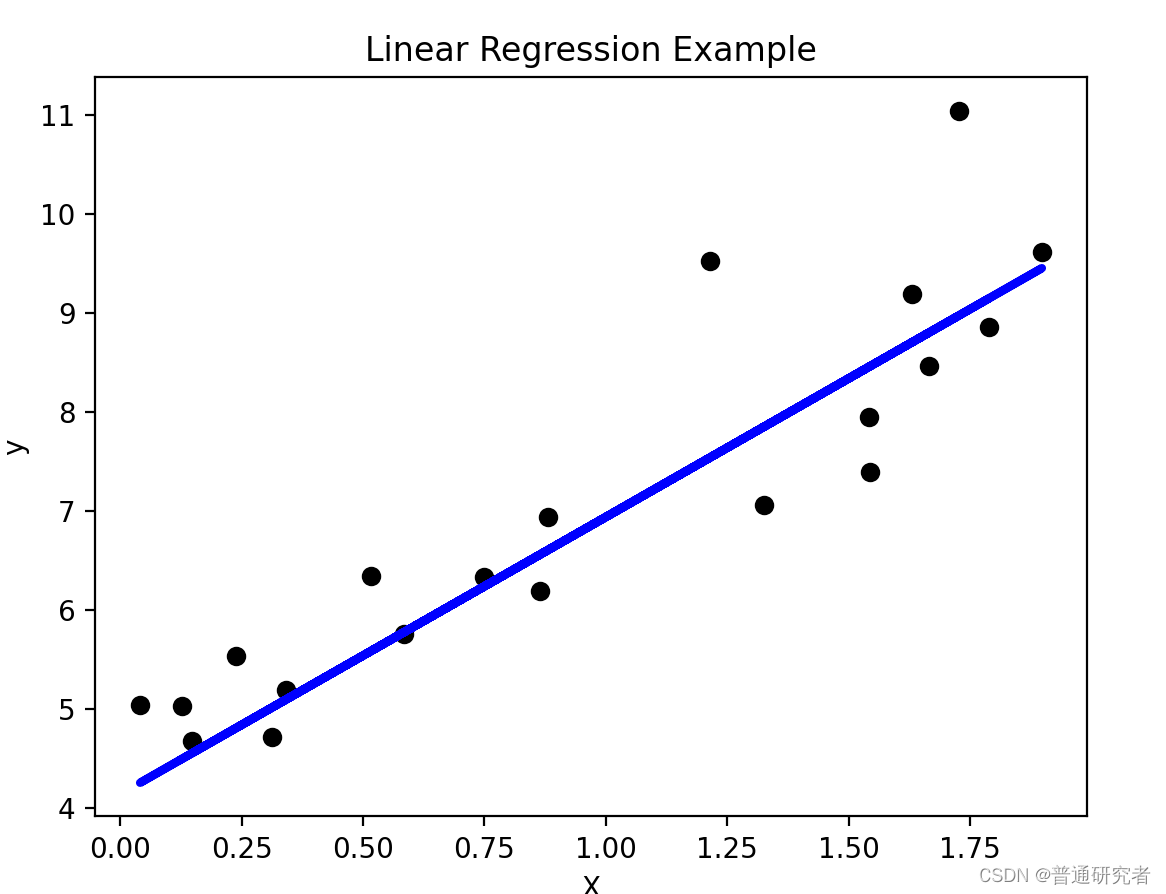
理解线性模型的关键点包括以下几个方面:
1. 基本形式:线性模型的基本形式是通过线性组合表示输入特征和权重,加上一个截距项。这基本方程是模型的基础。
2. 权重和截距:模型中的权重和截距决定了特征对输出的影响程度。权重越大,对应特征对输出的影响越大。
3. 损失函数:训练线性模型通常涉及到定义和优化一个损失函数,目标是使预测值与真实值之间的误差最小化。均方误差是线性回归中常用的损失函数。
4. 优化算法:通过使用梯度下降等优化算法,模型的权重和截距可以被调整,以最小化损失函数。这是模型训练的关键步骤。
5. 适用领域:线性模型在回归和分类问题中广泛应用。线性回归用于预测连续数值,而逻辑回归用于二分类问题。
6. 特殊情况:岭回归和Lasso回归是线性模型的变体,用于处理共线性和过拟合问题。它们通过引入正则化项来限制模型参数的大小。
7. 局限性:线性模型的局限性在于它们无法捕捉复杂的非线性关系。在处理非线性问题时,可能需要考虑其他更复杂的模型。
8. 解释性:线性模型具有较强的解释性,可以通过权重的大小和符号解释特征对输出的影响。这使得在一些应用场景中,如金融和医疗领域,线性模型仍然是有用的。
总体而言,线性模型是机器学习中一个重要的基础概念,理解线性模型有助于深入理解机器学习的核心原理。