1. 写在前面

  对于爬虫开发者来说，职业生涯中可能或多或少会遇到各种各样的网站，其中有些必要要求登陆才能浏览。那么模拟登陆的时候发现提交的登陆信息（用户名、密码）都是经过加密后的，如何处理？这里找到了一个网站案例，正所谓换汤不换药，案例的参考是逆向技巧与方法积累的重要补给

目标站点：

aHR0cDovL2xvZ2luLndzZ2pwLmNvbS5jbi8=

2. 分析请求

本次我们的目标则是针对登陆提交的表单信息（用户名、密码）加密进行一个逆向的分析，所以我们直接先随意构造一个不存在的信息点击提交然后进行抓包分析：

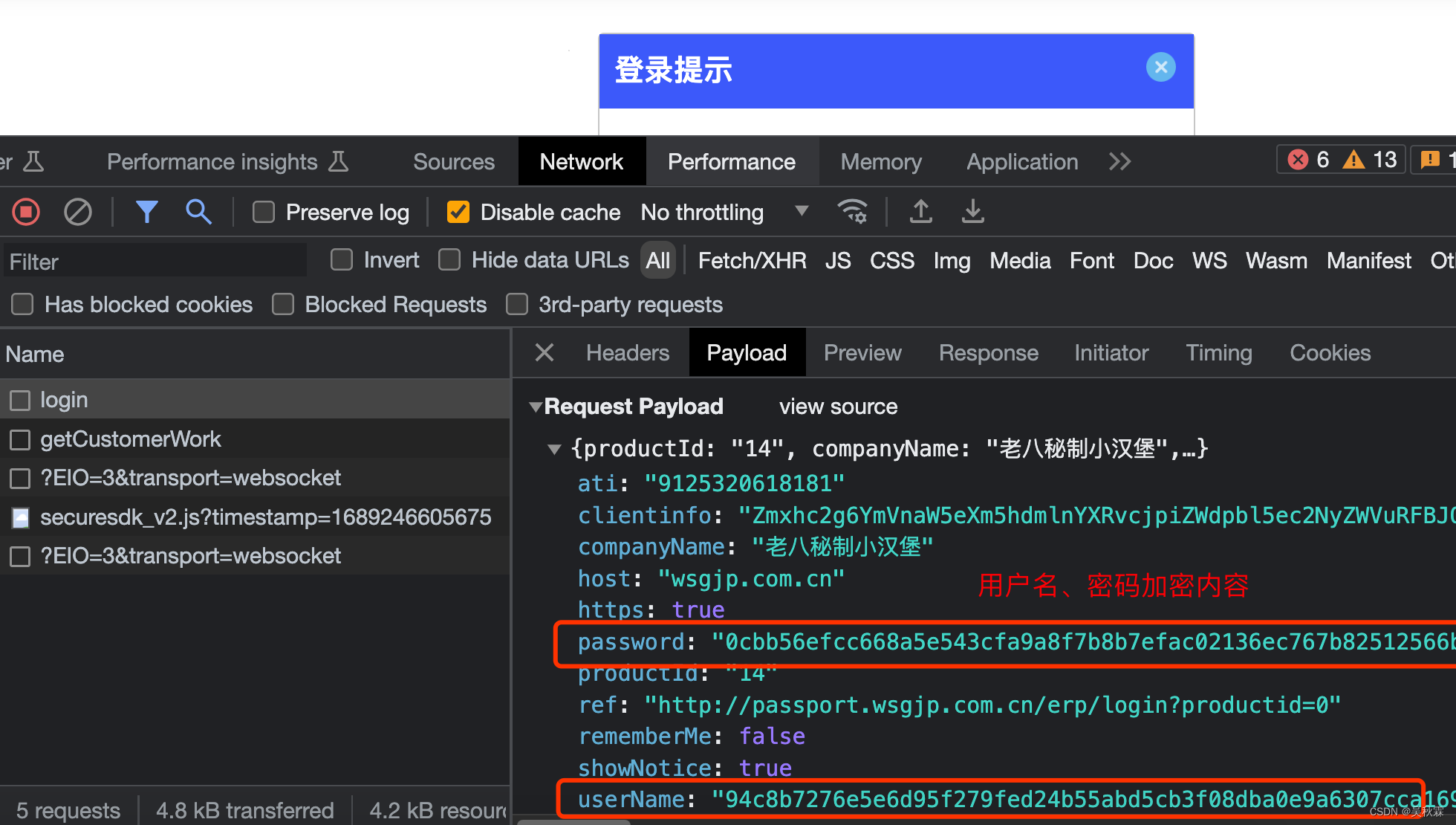
这里需要说的一下对于我们新手来说我们在JS逆向分析的时候，如何才能快速的找到请求的URL，有时候请求的URL是非常多的，可能少到几十多到上百个

我们如何快速的筛选与甄别，比如善用关键词搜索：

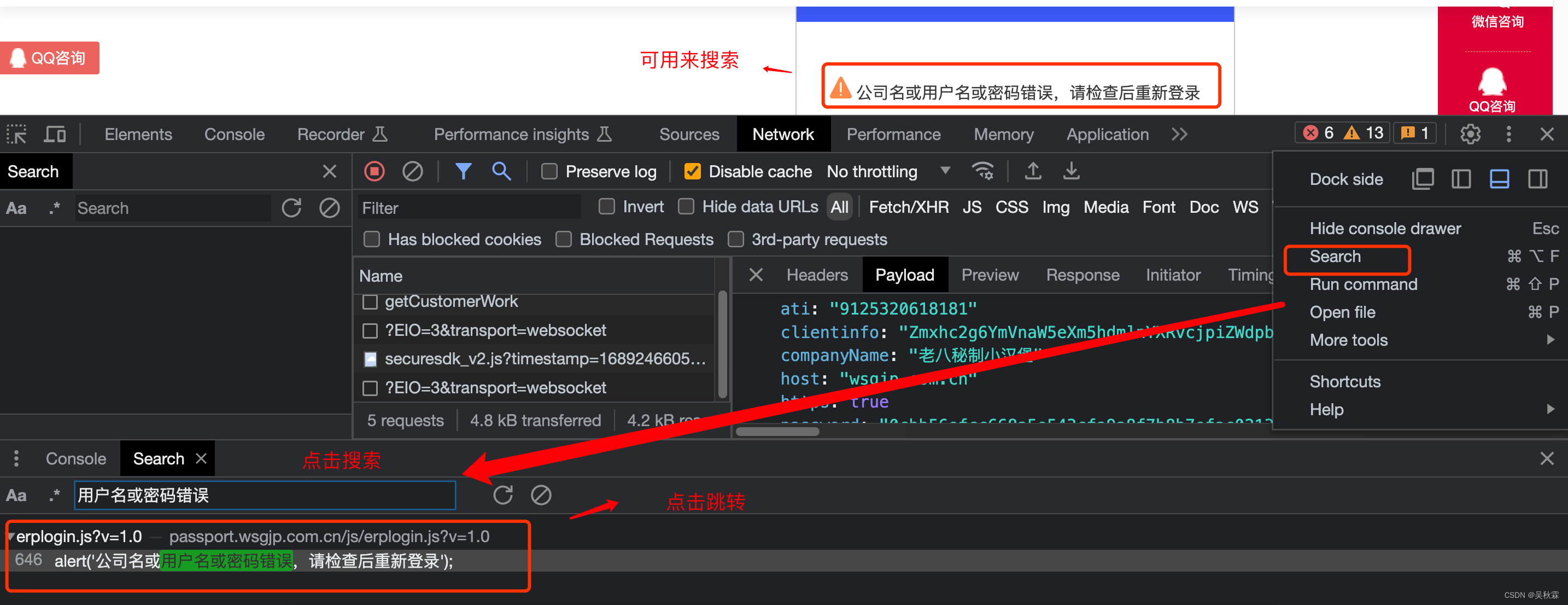
因为所有的提交点击操作请求都会发送到服务器，服务器再把数据发送过来渲染到网站上，所以上面反馈的信息，必定是经过某URLl请求过来的

3. 找加密点

接下来我们就是要找到上面的用户名跟密码是如何加密的，按照上述方式我们将password当成关键词搜索：

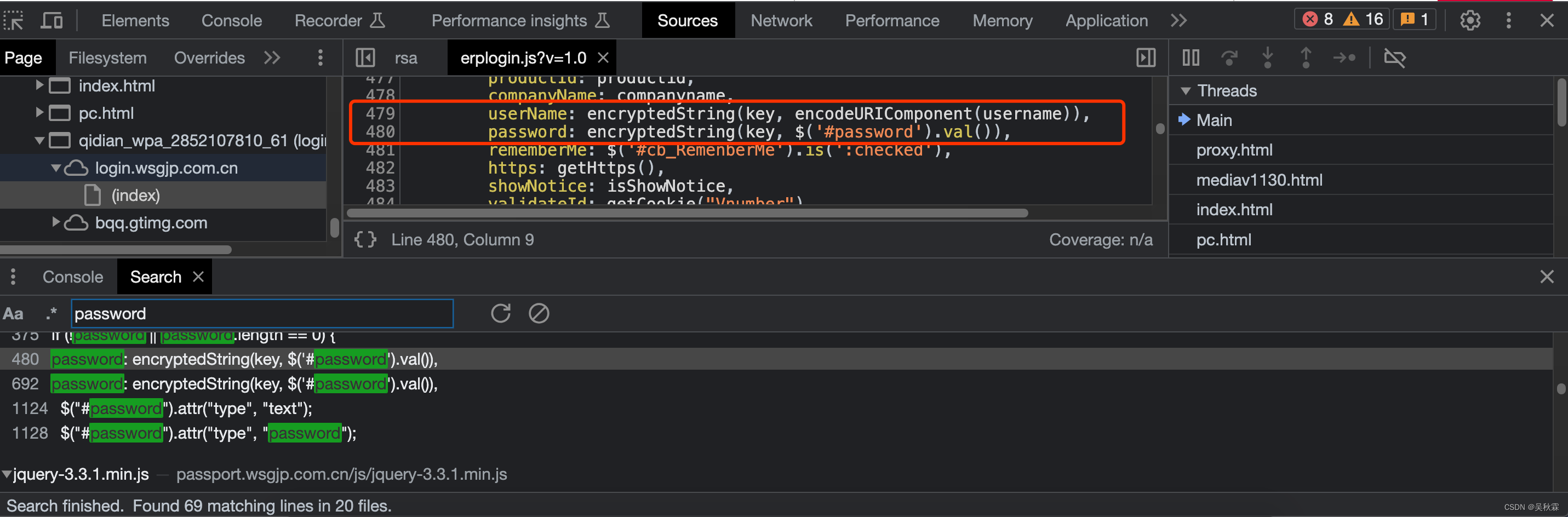
在这里可以看到有时候搜索出来可能有多个文件都带有我们搜索的password，这种情况如果是新手经验不多，那么我们就慢慢的看、分析与发现。例如上图绿色加深的关键词处js文件内有加密字样的代码，就跟我们使用排查法一样，加密解密这些特征词都是我们找寻的对象

我们可以看搜索到的这两行加密调用代码：

userName: encryptedString(key, encodeURIComponent(username)),
password: encryptedString(key, $('#password').val()),

这两行代码只有我们断点分析以后才能知道是不是我们要找的加密点，因为在搜索的时候可以看到很多时候多个文件中都存在这些关键词，有的JS中并没有使用

好的，现在我们来断点分析一下：

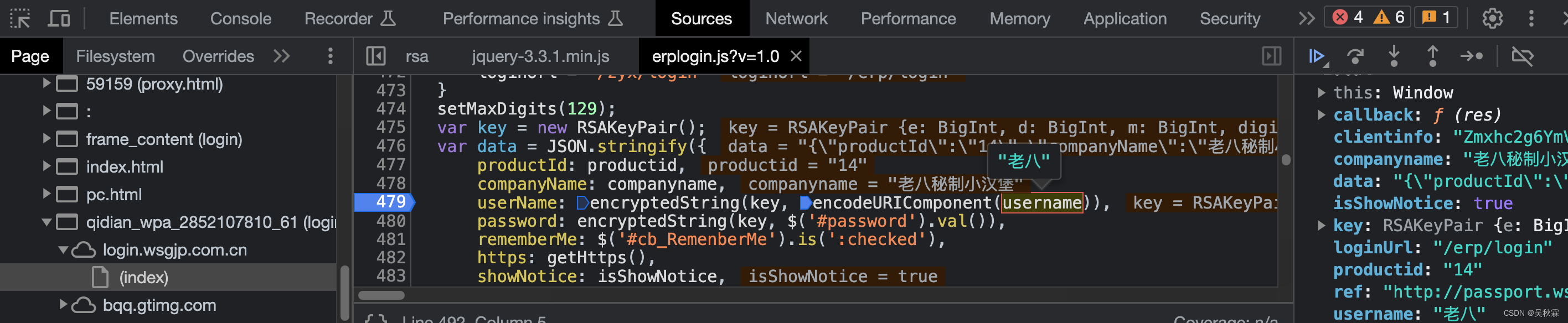
设置完断点后，我们再次提交一次登陆信息，可以看到断点停留在了479行断点处。我们将鼠标停留可以看到userName跟password加密值都是由encryptedString的两处生成

有时候在做JS逆向分析的时候善用控制台调试能够帮助我们更直观判断我们的推断，这个小Tips大家一定要记住！我们把加密函数放到Console控制台输出看一下：

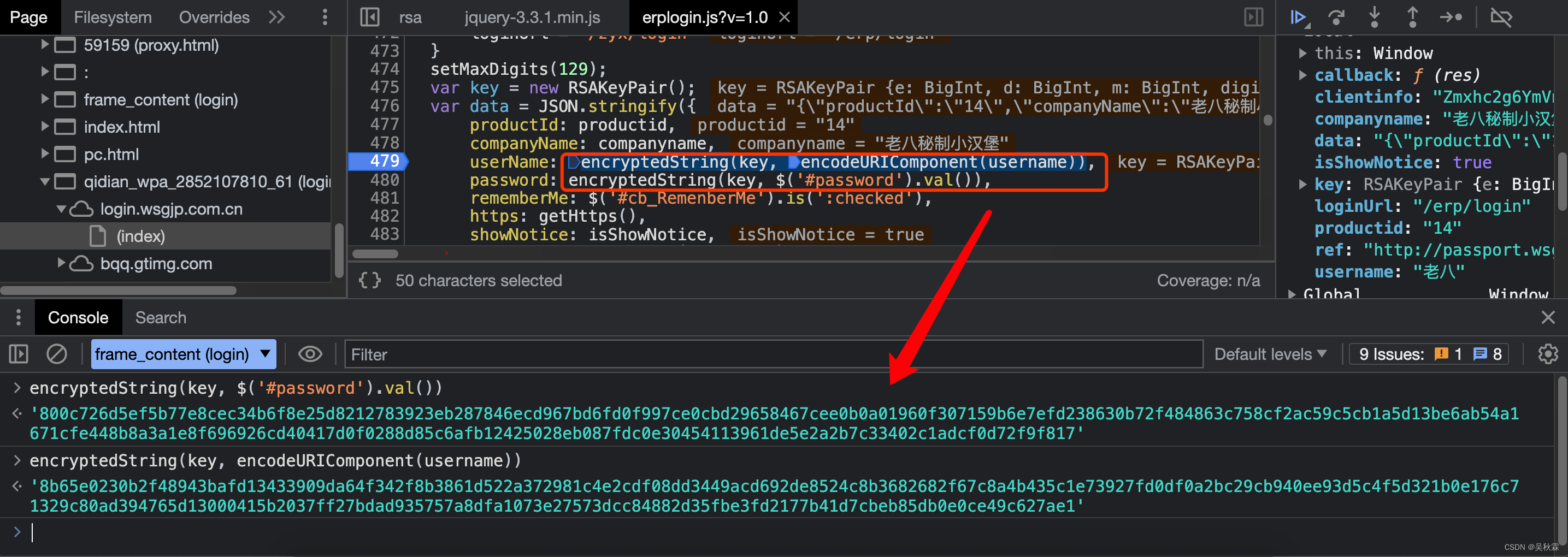
我们可以看到加密调用是在setMaxDigits这个函数里面并且在加密之前还调用了RSAKeyPair函数，所以这两函数也是需要扣的，加最后调用的encryptedString加密函数

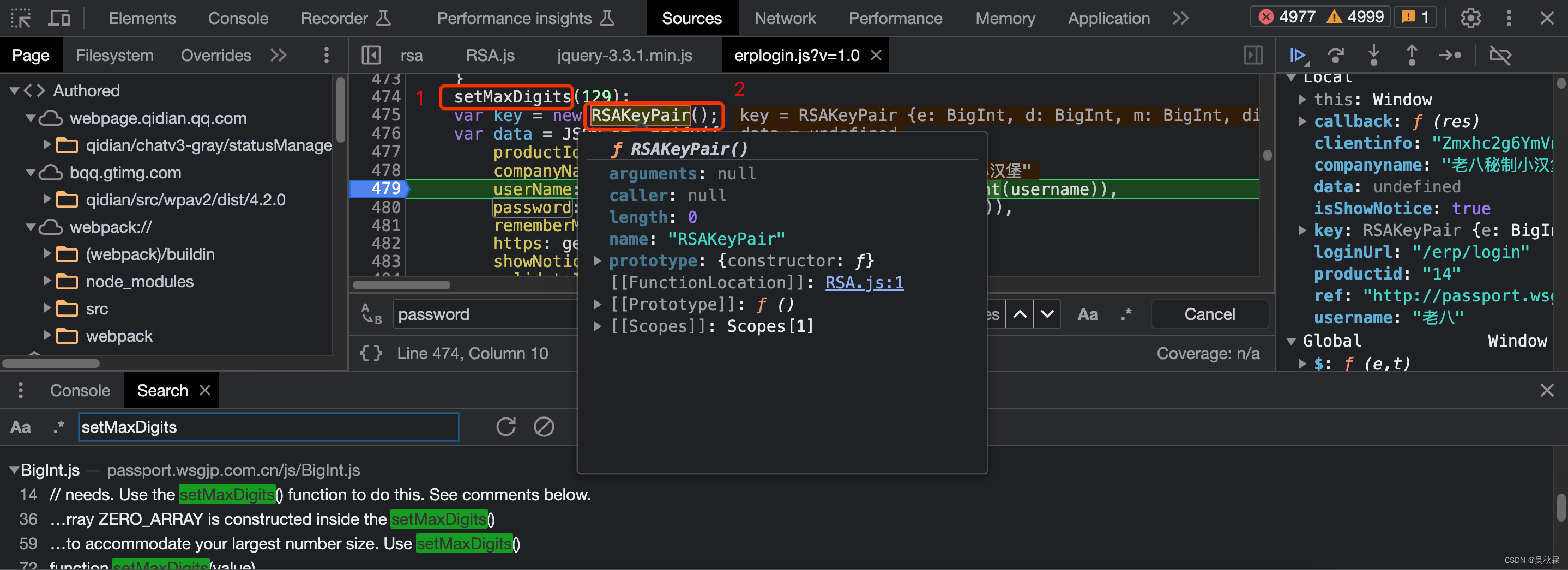
4. 扣代码

扣代码，主要扣取的就是目标代码内的逻辑与算法！在扣取代码的时候，只需要将鼠标移动至函数名上，如上图所示会弹出一个提示框点击跳转即可到目标函数，可以发现这几个函数的代码并不多，大约在几百行需要注意的是扣JS代码的时候有些时候代码量非常庞大，切记不要一股脑的拿下来，很多都是无用的逻辑，严重影响效率

function RSAKeyPair() {var encryptionExponent = "010001";var decryptionExponent = "";var modulus = "9A568982EE4BF010C38B5195A6F2DC7D66D5E6C02098CF25044CDD031AC08C6569D7063BB8959CB3FCB5AF572DE355AFA684AF7187948744E673275B494F394AF7F158841CA8B63BF65F185883F8D773A57ED731EDCD1AF2E0E57CD45F5F3CB4EBDD38F4A267E5ED02E7B44B93EDFFDADBDC8368019CD496BEC735BAF9E57125";this.e = biFromHex(encryptionExponent);this.d = biFromHex(decryptionExponent);this.m = biFromHex(modulus);this.digitSize = 2 * biHighIndex(this.m) + 2;this.chunkSize = this.digitSize - 11;this.radix = 16;this.barrett = new BarrettMu(this.m);
}function twoDigit(n) {return (n < 10 ? "0" : "") + String(n);
}function encryptedString(key, s) {if (key.chunkSize > key.digitSize - 11) {return "Error";}var a = new Array();var sl = s.length;var i = 0;while (i < sl) {a[i] = s.charCodeAt(i);i++;}var al = a.length;var result = "";var j, k, block;for (i = 0; i < al; i += key.chunkSize) {block = new BigInt();j = 0;var x;var msgLength = (i + key.chunkSize) > al ? al % key.chunkSize : key.chunkSize;var b = new Array();for (x = 0; x < msgLength; x++) {b[x] = a[i + msgLength - 1 - x];}b[msgLength] = 0; // markervar paddedSize = Math.max(8, key.digitSize - 3 - msgLength);for (x = 0; x < paddedSize; x++) {b[msgLength + 1 + x] = Math.floor(Math.random() * 254) + 1;}b[key.digitSize - 2] = 2; // markerb[key.digitSize - 1] = 0; // markerfor (k = 0; k < key.digitSize; ++j) {block.digits[j] = b[k++];block.digits[j] += b[k++] << 8;}var crypt = key.barrett.powMod(block, key.e);var text = key.radix == 16 ? biToHex(crypt) : biToString(crypt, key.radix);result += text + " ";}return result.substring(0, result.length - 1); // Remove last space.
}var biRadixBase = 2;
var biRadixBits = 16;
var bitsPerDigit = biRadixBits;
var biRadix = 1 << 16; // = 2^16 = 65536
var biHalfRadix = biRadix >>> 1;
var biRadixSquared = biRadix * biRadix;
var maxDigitVal = biRadix - 1;
var maxInteger = 9999999999999998;var maxDigits;
var ZERO_ARRAY;
var bigZero, bigOne;function setMaxDigits(value)
{maxDigits = value;ZERO_ARRAY = new Array(maxDigits);for (var iza = 0; iza < ZERO_ARRAY.length; iza++) ZERO_ARRAY[iza] = 0;bigZero = new BigInt();bigOne = new BigInt();bigOne.digits[0] = 1;
}setMaxDigits(20);// The maximum number of digits in base 10 you can convert to an
// integer without JavaScript throwing up on you.
var dpl10 = 15;
// lr10 = 10 ^ dpl10
var lr10 = biFromNumber(1000000000000000);function BigInt(flag)
{if (typeof flag == "boolean" && flag == true) {this.digits = null;}else {this.digits = ZERO_ARRAY.slice(0);}this.isNeg = false;
}function biFromDecimal(s)
{var isNeg = s.charAt(0) == '-';var i = isNeg ? 1 : 0;var result;// Skip leading zeros.while (i < s.length && s.charAt(i) == '0') ++i;if (i == s.length) {result = new BigInt();}else {var digitCount = s.length - i;var fgl = digitCount % dpl10;if (fgl == 0) fgl = dpl10;result = biFromNumber(Number(s.substr(i, fgl)));i += fgl;while (i < s.length) {result = biAdd(biMultiply(result, lr10),biFromNumber(Number(s.substr(i, dpl10))));i += dpl10;}result.isNeg = isNeg;}return result;
}function biCopy(bi)
{var result = new BigInt(true);result.digits = bi.digits.slice(0);result.isNeg = bi.isNeg;return result;
}function biFromNumber(i)
{var result = new BigInt();result.isNeg = i < 0;i = Math.abs(i);var j = 0;while (i > 0) {result.digits[j++] = i & maxDigitVal;i = Math.floor(i / biRadix);}return result;
}function reverseStr(s)
{var result = "";for (var i = s.length - 1; i > -1; --i) {result += s.charAt(i);}return result;
}var hexatrigesimalToChar = new Array('0', '1', '2', '3', '4', '5', '6', '7', '8', '9','a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j','k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't','u', 'v', 'w', 'x', 'y', 'z'
);function biToString(x, radix)
// 2 <= radix <= 36
{var b = new BigInt();b.digits[0] = radix;var qr = biDivideModulo(x, b);var result = hexatrigesimalToChar[qr[1].digits[0]];while (biCompare(qr[0], bigZero) == 1) {qr = biDivideModulo(qr[0], b);digit = qr[1].digits[0];result += hexatrigesimalToChar[qr[1].digits[0]];}return (x.isNeg ? "-" : "") + reverseStr(result);
}function biToDecimal(x)
{var b = new BigInt();b.digits[0] = 10;var qr = biDivideModulo(x, b);var result = String(qr[1].digits[0]);while (biCompare(qr[0], bigZero) == 1) {qr = biDivideModulo(qr[0], b);result += String(qr[1].digits[0]);}return (x.isNeg ? "-" : "") + reverseStr(result);
}var hexToChar = new Array('0', '1', '2', '3', '4', '5', '6', '7', '8', '9','a', 'b', 'c', 'd', 'e', 'f');function digitToHex(n)
{var mask = 0xf;var result = "";for (i = 0; i < 4; ++i) {result += hexToChar[n & mask];n >>>= 4;}return reverseStr(result);
}function biToHex(x)
{var result = "";var n = biHighIndex(x);for (var i = biHighIndex(x); i > -1; --i) {result += digitToHex(x.digits[i]);}return result;
}function charToHex(c)
{var ZERO = 48;var NINE = ZERO + 9;var littleA = 97;var littleZ = littleA + 25;var bigA = 65;var bigZ = 65 + 25;var result;if (c >= ZERO && c <= NINE) {result = c - ZERO;} else if (c >= bigA && c <= bigZ) {result = 10 + c - bigA;} else if (c >= littleA && c <= littleZ) {result = 10 + c - littleA;} else {result = 0;}return result;
}function hexToDigit(s)
{var result = 0;var sl = Math.min(s.length, 4);for (var i = 0; i < sl; ++i) {result <<= 4;result |= charToHex(s.charCodeAt(i))}return result;
}function biFromHex(s)
{var result = new BigInt();var sl = s.length;for (var i = sl, j = 0; i > 0; i -= 4, ++j) {result.digits[j] = hexToDigit(s.substr(Math.max(i - 4, 0), Math.min(i, 4)));}return result;
}function biFromString(s, radix)
{var isNeg = s.charAt(0) == '-';var istop = isNeg ? 1 : 0;var result = new BigInt();var place = new BigInt();place.digits[0] = 1; // radix^0for (var i = s.length - 1; i >= istop; i--) {var c = s.charCodeAt(i);var digit = charToHex(c);var biDigit = biMultiplyDigit(place, digit);result = biAdd(result, biDigit);place = biMultiplyDigit(place, radix);}result.isNeg = isNeg;return result;
}function biDump(b)
{return (b.isNeg ? "-" : "") + b.digits.join(" ");
}function biAdd(x, y)
{var result;if (x.isNeg != y.isNeg) {y.isNeg = !y.isNeg;result = biSubtract(x, y);y.isNeg = !y.isNeg;}else {result = new BigInt();var c = 0;var n;for (var i = 0; i < x.digits.length; ++i) {n = x.digits[i] + y.digits[i] + c;result.digits[i] = n % biRadix;c = Number(n >= biRadix);}result.isNeg = x.isNeg;}return result;
}function biSubtract(x, y)
{var result;if (x.isNeg != y.isNeg) {y.isNeg = !y.isNeg;result = biAdd(x, y);y.isNeg = !y.isNeg;} else {result = new BigInt();var n, c;c = 0;for (var i = 0; i < x.digits.length; ++i) {n = x.digits[i] - y.digits[i] + c;result.digits[i] = n % biRadix;// Stupid non-conforming modulus operation.if (result.digits[i] < 0) result.digits[i] += biRadix;c = 0 - Number(n < 0);}// Fix up the negative sign, if any.if (c == -1) {c = 0;for (var i = 0; i < x.digits.length; ++i) {n = 0 - result.digits[i] + c;result.digits[i] = n % biRadix;// Stupid non-conforming modulus operation.if (result.digits[i] < 0) result.digits[i] += biRadix;c = 0 - Number(n < 0);}// Result is opposite sign of arguments.result.isNeg = !x.isNeg;} else {// Result is same sign.result.isNeg = x.isNeg;}}return result;
}function biHighIndex(x)
{var result = x.digits.length - 1;while (result > 0 && x.digits[result] == 0) --result;return result;
}function biNumBits(x)
{var n = biHighIndex(x);var d = x.digits[n];var m = (n + 1) * bitsPerDigit;var result;for (result = m; result > m - bitsPerDigit; --result) {if ((d & 0x8000) != 0) break;d <<= 1;}return result;
}function biMultiply(x, y)
{var result = new BigInt();var c;var n = biHighIndex(x);var t = biHighIndex(y);var u, uv, k;for (var i = 0; i <= t; ++i) {c = 0;k = i;for (j = 0; j <= n; ++j, ++k) {uv = result.digits[k] + x.digits[j] * y.digits[i] + c;result.digits[k] = uv & maxDigitVal;c = uv >>> biRadixBits;//c = Math.floor(uv / biRadix);}result.digits[i + n + 1] = c;}// Someone give me a logical xor, please.result.isNeg = x.isNeg != y.isNeg;return result;
}function biMultiplyDigit(x, y)
{var n, c, uv;result = new BigInt();n = biHighIndex(x);c = 0;for (var j = 0; j <= n; ++j) {uv = result.digits[j] + x.digits[j] * y + c;result.digits[j] = uv & maxDigitVal;c = uv >>> biRadixBits;//c = Math.floor(uv / biRadix);}result.digits[1 + n] = c;return result;
}function arrayCopy(src, srcStart, dest, destStart, n)
{var m = Math.min(srcStart + n, src.length);for (var i = srcStart, j = destStart; i < m; ++i, ++j) {dest[j] = src[i];}
}var highBitMasks = new Array(0x0000, 0x8000, 0xC000, 0xE000, 0xF000, 0xF800,0xFC00, 0xFE00, 0xFF00, 0xFF80, 0xFFC0, 0xFFE0,0xFFF0, 0xFFF8, 0xFFFC, 0xFFFE, 0xFFFF);function biShiftLeft(x, n)
{var digitCount = Math.floor(n / bitsPerDigit);var result = new BigInt();arrayCopy(x.digits, 0, result.digits, digitCount,result.digits.length - digitCount);var bits = n % bitsPerDigit;var rightBits = bitsPerDigit - bits;for (var i = result.digits.length - 1, i1 = i - 1; i > 0; --i, --i1) {result.digits[i] = ((result.digits[i] << bits) & maxDigitVal) |((result.digits[i1] & highBitMasks[bits]) >>>(rightBits));}result.digits[0] = ((result.digits[i] << bits) & maxDigitVal);result.isNeg = x.isNeg;return result;
}var lowBitMasks = new Array(0x0000, 0x0001, 0x0003, 0x0007, 0x000F, 0x001F,0x003F, 0x007F, 0x00FF, 0x01FF, 0x03FF, 0x07FF,0x0FFF, 0x1FFF, 0x3FFF, 0x7FFF, 0xFFFF);function biShiftRight(x, n)
{var digitCount = Math.floor(n / bitsPerDigit);var result = new BigInt();arrayCopy(x.digits, digitCount, result.digits, 0,x.digits.length - digitCount);var bits = n % bitsPerDigit;var leftBits = bitsPerDigit - bits;for (var i = 0, i1 = i + 1; i < result.digits.length - 1; ++i, ++i1) {result.digits[i] = (result.digits[i] >>> bits) |((result.digits[i1] & lowBitMasks[bits]) << leftBits);}result.digits[result.digits.length - 1] >>>= bits;result.isNeg = x.isNeg;return result;
}function biMultiplyByRadixPower(x, n)
{var result = new BigInt();arrayCopy(x.digits, 0, result.digits, n, result.digits.length - n);return result;
}function biDivideByRadixPower(x, n)
{var result = new BigInt();arrayCopy(x.digits, n, result.digits, 0, result.digits.length - n);return result;
}function biModuloByRadixPower(x, n)
{var result = new BigInt();arrayCopy(x.digits, 0, result.digits, 0, n);return result;
}function biCompare(x, y)
{if (x.isNeg != y.isNeg) {return 1 - 2 * Number(x.isNeg);}for (var i = x.digits.length - 1; i >= 0; --i) {if (x.digits[i] != y.digits[i]) {if (x.isNeg) {return 1 - 2 * Number(x.digits[i] > y.digits[i]);} else {return 1 - 2 * Number(x.digits[i] < y.digits[i]);}}}return 0;
}function biDivideModulo(x, y)
{var nb = biNumBits(x);var tb = biNumBits(y);var origYIsNeg = y.isNeg;var q, r;if (nb < tb) {// |x| < |y|if (x.isNeg) {q = biCopy(bigOne);q.isNeg = !y.isNeg;x.isNeg = false;y.isNeg = false;r = biSubtract(y, x);// Restore signs, 'cause they're references.x.isNeg = true;y.isNeg = origYIsNeg;} else {q = new BigInt();r = biCopy(x);}return new Array(q, r);}q = new BigInt();r = x;// Normalize Y.var t = Math.ceil(tb / bitsPerDigit) - 1;var lambda = 0;while (y.digits[t] < biHalfRadix) {y = biShiftLeft(y, 1);++lambda;++tb;t = Math.ceil(tb / bitsPerDigit) - 1;}// Shift r over to keep the quotient constant. We'll shift the// remainder back at the end.r = biShiftLeft(r, lambda);nb += lambda; // Update the bit count for x.var n = Math.ceil(nb / bitsPerDigit) - 1;var b = biMultiplyByRadixPower(y, n - t);while (biCompare(r, b) != -1) {++q.digits[n - t];r = biSubtract(r, b);}for (var i = n; i > t; --i) {var ri = (i >= r.digits.length) ? 0 : r.digits[i];var ri1 = (i - 1 >= r.digits.length) ? 0 : r.digits[i - 1];var ri2 = (i - 2 >= r.digits.length) ? 0 : r.digits[i - 2];var yt = (t >= y.digits.length) ? 0 : y.digits[t];var yt1 = (t - 1 >= y.digits.length) ? 0 : y.digits[t - 1];if (ri == yt) {q.digits[i - t - 1] = maxDigitVal;} else {q.digits[i - t - 1] = Math.floor((ri * biRadix + ri1) / yt);}var c1 = q.digits[i - t - 1] * ((yt * biRadix) + yt1);var c2 = (ri * biRadixSquared) + ((ri1 * biRadix) + ri2);while (c1 > c2) {--q.digits[i - t - 1];c1 = q.digits[i - t - 1] * ((yt * biRadix) | yt1);c2 = (ri * biRadix * biRadix) + ((ri1 * biRadix) + ri2);}b = biMultiplyByRadixPower(y, i - t - 1);r = biSubtract(r, biMultiplyDigit(b, q.digits[i - t - 1]));if (r.isNeg) {r = biAdd(r, b);--q.digits[i - t - 1];}}r = biShiftRight(r, lambda);// Fiddle with the signs and stuff to make sure that 0 <= r < y.q.isNeg = x.isNeg != origYIsNeg;if (x.isNeg) {if (origYIsNeg) {q = biAdd(q, bigOne);} else {q = biSubtract(q, bigOne);}y = biShiftRight(y, lambda);r = biSubtract(y, r);}// Check for the unbelievably stupid degenerate case of r == -0.if (r.digits[0] == 0 && biHighIndex(r) == 0) r.isNeg = false;return new Array(q, r);
}function biDivide(x, y)
{return biDivideModulo(x, y)[0];
}function biModulo(x, y)
{return biDivideModulo(x, y)[1];
}function biMultiplyMod(x, y, m)
{return biModulo(biMultiply(x, y), m);
}function biPow(x, y)
{var result = bigOne;var a = x;while (true) {if ((y & 1) != 0) result = biMultiply(result, a);y >>= 1;if (y == 0) break;a = biMultiply(a, a);}return result;
}function biPowMod(x, y, m)
{var result = bigOne;var a = x;var k = y;while (true) {if ((k.digits[0] & 1) != 0) result = biMultiplyMod(result, a, m);k = biShiftRight(k, 1);if (k.digits[0] == 0 && biHighIndex(k) == 0) break;a = biMultiplyMod(a, a, m);}return result;
}

上面这堆JS则是实现加密算法的代码，这里看了一下代码做一个简单的分析，虽然我们没有必要深入了解太多加密算法的逻辑，但是如果能够知其然并知其所以然，那我们也能自己用其他的方式或者语言实现它的整个加密算法：

• RSAKeyPair这个函数它定义了一个RSA密钥对，可以看到encryptionExponent 是公钥，decryptionExponent 是私钥，然后通过调用其他函数，将公私钥指数和其他变量存储在 RSA 密钥的对象中
• encryptedString函数主要实现了字符串的一些个加密操作，接受密钥和字符串作为参数。检查密钥的 chunkSize是否合法，并将字符串转换为字符数组，根据chunkSize将字符数组分块加密。加密过程中，使用随机生成的填充数据再返回加密后的字符串
• BigInt函数是一个大整数类，用于处理大数运算。它包含了大整数的属性和方法，例如创建大整数、复制大整数、比较大小、相加、相减等操作
• biFromHex函数将十六进制字符串转换为大整数。它从字符串的末尾开始，每四位转换为一个十进制数字，并将其存储在大整数对象的 digits 属性中
• biMultiply函数实现了两个大整数的乘法运算。它使用传统的竖式乘法算法，逐位相乘并考虑进位
• biModulo函数计算两个大整数的模运算结果，即返回除法的余数部分
• biPowMod函数计算大整数的幂模运算结果。它使用快速幂算法来提高计算效率

它们干的一件事：共同组成了一个简单的RSA加密算法

这里可以看到密码加密处的$(‘#password’)表示密码输入框的jQuery选择器，通过模拟用户输入来传递参数。所以我们这里需要简单的写两个测试函数调用验证一下即可：

// 用户名加密
function UsernameEncryption(username) {setMaxDigits(129);var key = new RSAKeyPair();return encryptedString(key, encodeURIComponent(username))
}// 密码加密
function PasswordEncryption() {setMaxDigits(129);var key = new RSAKeyPair();var password = '123456'$('#password').val(password);return encryptedString(key, $('#password').val())
}

接下来直接把上面的封装好的JS代码放到调试工具测试即可，JS的调试工具还是比较多的，这里我们主要是思路，验证的话还是在控制台输出一下（扣代码的时候缺什么就补什么）：

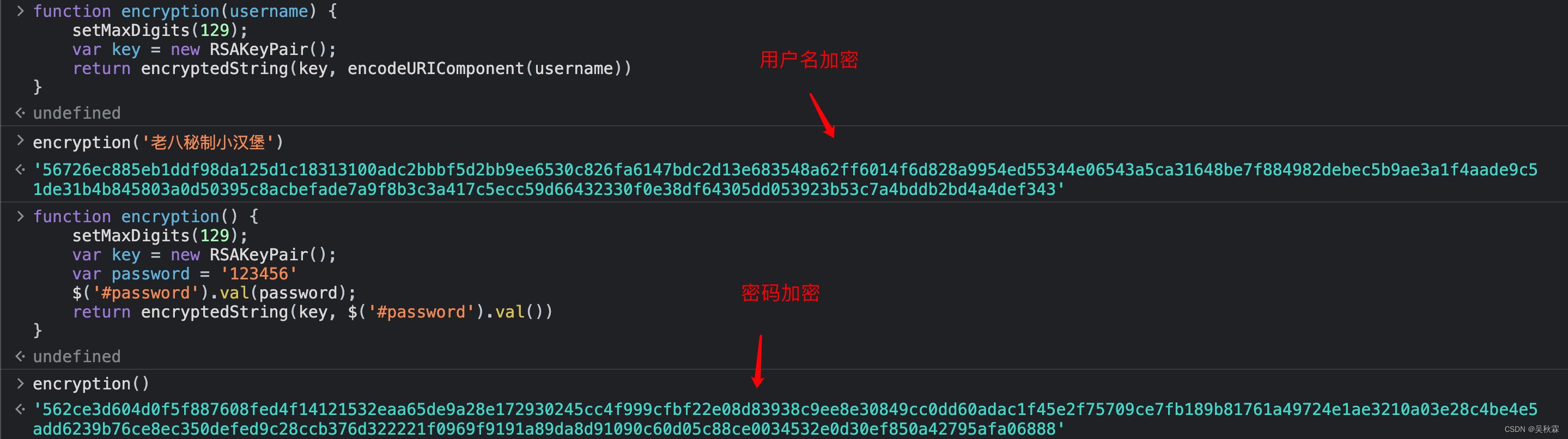
到了这里我们就完整的拿到了登陆提交信息的加密方案，以上的所扣取的JS代码可以放到我们Python代码中调用，也可以自己实现当然肯定有一定的难度，一般大部分的JS逆向工作中都是直接调用的方式

这是一个非常简单的案例，在找加密点扣取对应JS代码这些都没有太大的难度，都是一些JS逆向中常见技巧

  好了，到这里又到了跟大家说再见的时候了。创作不易，帮忙点个赞再走吧。你的支持是我创作的动力，希望能带给大家更多优质的文章