一、绘制
(一)颜色
- 颜色混合
vec3 colorA = vec3(0.149,0.141,0.912);
vec3 colorB = vec3(1.000,0.833,0.224);//pct:混合因子float pct = abs(sin(u_time));
//mix():将两个颜色进行混合,实现伴随时间变化的过渡效果color = mix(colorA, colorB, pct);
这种表示某个值的变化情况的函数叫做缓动函数、
- 颜色渐变
vec3 colorA = vec3(0.149,0.141,0.912);
vec3 colorB = vec3(1.000,0.833,0.224);//pct: 混合因子
vec3 pct = vec3(st.x); //伴随着x轴的增长,混合因子越大
//mix():将两个颜色进行混合,实现伴随x轴变化的过渡效果
color = mix(colorA, colorB, pct);
-
HSB颜色空间
H:色相 S:饱和度 B:亮度值 更符合直觉也更利于组织颜色 -
极坐标下的HSB
HSB原本是在极坐标下产生的(以半径和角度)而非基于xy的笛卡尔坐标系。
(二)形状
- 长方形
//if-else的方法if ( (X GREATER THAN 1) AND (Y GREATER THAN 1) )paint whiteelsepaint black
//step的方法
vec2 st = gl_FragCoord.xy/u_resolution.xy;
vec3 color = vec3(0.0);
// bottom-left
vec2 bl = step(vec2(0.1),st);float pct = bl.x * bl.y; //等价于 AND// top-right
vec2 tr = step(vec2(0.1),1.0-st); //进行坐标转置
pct *= tr.x * tr.y;color = vec3(pct);gl_FragColor = vec4(color,1.0);
- 圆
通过到点的距离进行计算。常用的距离函数有:distance()函数
loat pct = 0.0;pct = distance(st,vec2(0.5)); //计算到圆心的距离
vec3 color = vec3(pct);gl_FragColor = vec4( color, 1.0);
- 距离场
通过空间距离来解释图形,例如越黑的地方代表海拔越高。
//极坐标的表示形式
vec2 pos = vec2(0.5)-st;
float r = length(pos)*2.0;
float a = atan(pos.y,pos.x);//输出对应的形状
f = abs(cos(a*12. + u_time)*sin(a*3.+ u_time))*.8+.1;
color = vec3( 1.-smoothstep(f,f+0.02,r) );
gl_FragColor = vec4(color, 1.0);
(三)矩阵
- 平移
在二维平面上,进行二维向量的相加即可
vec2 translate = vec2(cos(u_time),sin(u_time));st += translate*0.35;
- 旋转
构造旋转矩阵,通过传入要旋转的角度即可。
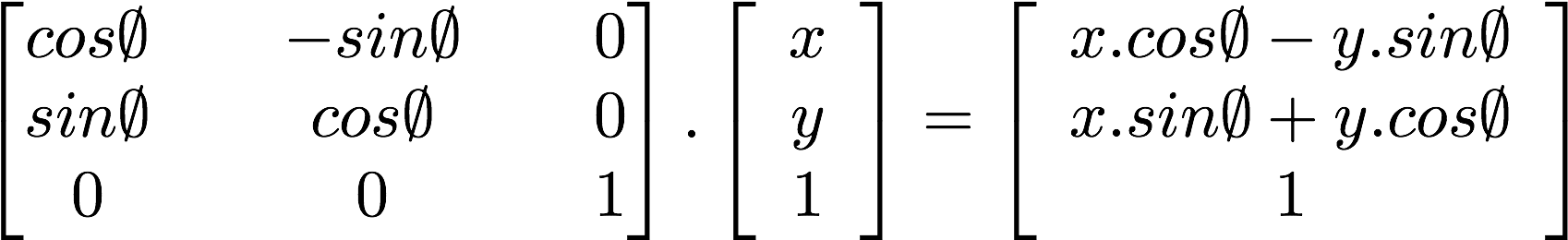
//可以利用x-y 坐标乘以旋转矩阵进行坐标变换
//旋转矩阵
mat2 rotate2d(float _angle){return mat2(cos(_angle),-sin(_angle),sin(_angle),cos(_angle));
}
//进行坐标旋转
st = rotate2d( sin(u_time)*PI) * st;
- 缩放
构造放缩矩阵,通过传入放缩因子即可
//构造放缩矩阵
mat2 scale(vec2 _scale){return mat2(_scale.x,0.0,0.0,_scale.y);
}
//进行放缩变换st = scale( vec2(sin(u_time)+1.0) ) * st;
- YUV色彩空间
//构造 rgb-yuv色彩转换矩阵
mat3 yuv2rgb = mat3(1.0, 0.0, 1.13983,1.0, -0.39465, -0.58060,1.0, 2.03211, 0.0);
//进行色域转换
color = yuv2rgb * vec3(0.5, st.x, st.y) ;
(四)模式
- 模式图案
标准的坐标空间为 0-1 区间,如果要映射出多个等比例的图块,那么可以将x-y 坐标进行等比例放大,再截取对应的小数部分即可得到多个 0-1区间的方块
vec2 st = gl_FragCoord.xy/u_resolution;
//坐标整体放缩
st *= 5.0;
//截取出小数部分
st = fract(st);
color = vec3(st,0.0);
gl_FragColor = vec4(color,1.0);
- 内部应用矩阵
//生成模式图案
vec2 tile(vec2 _st, float _zoom){_st *= _zoom;return fract(_st);
}
//定义旋转矩阵,进行旋转变换
vec2 rotate2D(vec2 _st, float _angle){_st -= 0.5;_st = mat2(cos(_angle),-sin(_angle),sin(_angle),cos(_angle)) * _st;_st += 0.5;return _st;
}
//绘制
st = tile(st,4.);
//内部进行旋转
st = rotate2D(st,PI*0.250);
//画方块
color = vec3(box(st,vec2(0.7),0.01));
- 偏移图案
- Truchet 瓷砖
二、生成
(一)随机
- 2D随机
在2D图案的随机中,需要将一个二维向量转换为一个一维的浮点数,主要是针对小数部分进行截取。
//利用dot和fract的结合可以即可以得到无序的浮点数序列
float random (vec2 st) {return fract(sin(dot(st.xy,vec2(12.9898,78.233)))*43758.5453123);
}
//
float rnd = random( st );
- floor函数
对于生成的2D噪点来说,在使用上可以对生成的地形坐标进行取整,降低随机生成噪点的精度。
vec2 st = gl_FragCoord.xy/u_resolution.xy;
st *= 10.0; // Scale the coordinate system by 10
vec2 ipos = floor(st); // get the integer coords
vec2 fpos = fract(st); // get the fractional coords
vec3 color = vec3(random( ipos ));
gl_FragColor = vec4(color,1.0);
(二)噪声
一种做法是将整数和小数部分进行截取,然后将原始位置的整数值进行一个随机化,再与原来的小数部分进行整合得到或离散或平滑的噪声波形。
- 一元噪声
float i = floor(x); // 整数(i 代表 integer)
float f = fract(x); // 小数(f 代表 fraction)
//y = rand(i); //rand() 在之前的章节提过
//y = mix(rand(i), rand(i + 1.0), f);
y = mix(rand(i), rand(i + 1.0), smoothstep(0.,1.,f));
- 2D Noise
对于2d的地图噪声来说,可以对场景进行一定的放缩后进行Floor化取整再进行随机。
float random (in vec2 st) {return fract(sin(dot(st.xy,vec2(12.9898,78.233)))* 43758.5453123);
}float noise (in vec2 st) {vec2 i = floor(st);vec2 f = fract(st);// Four corners in 2D of a tilefloat a = random(i);float b = random(i + vec2(1.0, 0.0));float c = random(i + vec2(0.0, 1.0));float d = random(i + vec2(1.0, 1.0));return mix(a, b, u.x) +(c - a)* u.y * (1.0 - u.x) +(d - b) * u.x * u.y;
}
- 生成式设计中的noise应用
如果利用随机值进行插值,那么得到的值是一个非常不连续的快状分布。如果要消除这种块状分布,那么可以根据梯度进行插值,也就是得到每一个像素的变化率。
方式1 与规则的纹理相结合形成漩涡状效果
方式2 与距离场结合,形成图案
方式3 用 noise 函数来变换一个形状
(三)网格噪声
- 平铺和迭代
将空间分割成网格,可以不需要计算每一个像素点到每一个特征点的距离,每一个网格对应一个特征点。
//分块
st *= 3.;
vec2 i_st = floor(st);
vec2 f_st = fract(st);
//随机生成特征点
vec2 point = random2(i_st);
//计算每一个像素到随机点的距离
vec2 diff = point - f_st;
float dist = length(diff);
-
维诺图算法
偏向于填充的思想在获得特征点过后通过距离判定得到划分后的维诺图。 -
优化维诺图方法
可以让常规噪声和维诺图进行融合