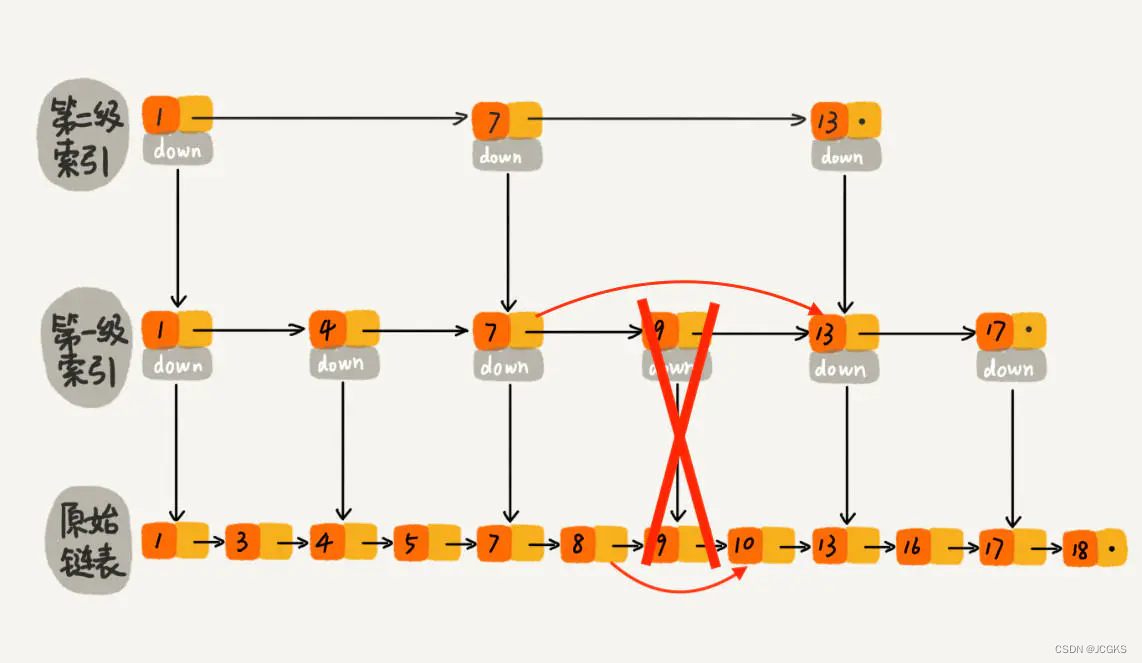
( A, B )---1*30*2---( 1, 0 )( 0, 1 )

让网络的输入只有1个节点，A，B训练集各只有1张图片，让A是0，B是1，统计迭代次数。

在收敛误差为7e-4的时候收敛199次，

差值结构			A-B	迭代次数
1			1-0	27191.925

得到收敛迭代次数平均值为27191.925.这个值和前面的实验值符合的很好。

差值结构			A-B	迭代次数
0	1	0	2*2*2-0*0*0	27189.46
0	1	0	2*2*2-0*0*0	27189.46
0	1	0	2*2*2-0*0*0	27189.46

如分类222-000的迭代次数为27189.因为全0列对迭代次数没有影响，因此222-000的差值结构的就是一个1不断的循环. 因此1-0和222-000的列排斥能应该是一样的，都是1.

所以如222-000这样没有全0行的差值结构的平均列的1的面值就是1，而不是同列1的数量和。因为这种结构的循环节长度就是1，空间的长度也是1.

现在继续做实验增加全0行，改变空间的长度，观察空间尺寸的变换对迭代次数的影响。

得到表格

	0.8		等效排斥能		迭代次数/199		1	2	3	4	5	6	7	8	9
		1	1	1.00	27191.92		1
1.51	1.6	2	0.66	1.51	41112.98		1	0
2.33	2.4	3	0.43	2.33	63402.22		1	0	0
3.13	3.2	4	0.32	3.13	85209.28		1	0	0	0
3.92	4	5	0.26	3.92	106483.11		1	0	0	0	0
4.77	4.8	6	0.21	4.77	129595.27		1	0	0	0	0	0
5.53	5.6	7	0.18	5.53	150370.22		1	0	0	0	0	0	0
6.35	6.4	8	0.16	6.35	172608.52		1	0	0	0	0	0	0	0
7.16	7.2	9	0.14	7.16	194685.29		1	0	0	0	0	0	0	0	0

如迭代次数63402对应的1，0，0，就是差值结构为1，0，0不断的循环。按照列排斥能的方法,这9组的排斥能应该是相同的因为他们的平均列相同都是1.

但结果很明显，全0行的增加会导致迭代次数变大。所以全0行的增加导致空间变大，等效也可以理解为全0行的增加导致差值结构变小。

这个放缩的系数约为

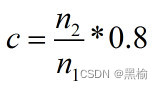
如有5个全0行，放缩系数为0.8*6/1=4.8.则等效列排斥能约为1/4.8=0.21.

所以计算这种含有全0行的差值结构的列排斥能的方法应为

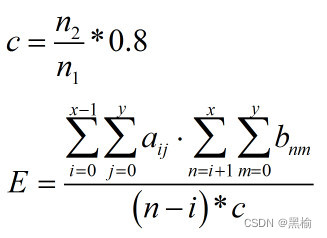
要考虑空间对结构的放缩效应。