大家好，我是怒码少年小码。

回溯是最重要的算法思想之一，主要解决一些暴力枚举也搞不定的问题（组合、子集、分割、排列、棋盘等等）。性能并不高，但是哪些暴力枚举都无法ko的问题能解出来就可以了🤣。

这一篇，让我们来看看回溯是个什么玩意儿😎。

回溯思想

定义

是一个种基于深度优先搜索的思想，在搜索过程中通过剪枝操作来减少搜索空间，从而找到问题的解。

回溯可以理解为递归的拓展，而代码结构又特别像深度遍历N叉树，因此只要知道递归，理解回溯并不难。

模板

回溯比其他思想好理解的一点就是它是有模板的，下面是伪代码：

void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择本层集合中元素（画成树，就是树节点孩子的大小）){处理节点;backtracking();回溯，撤销处理结果;}
}

---

本文我们只干一件事——分析回溯的模板🫡。

从树的遍历开始

透析一种基于深度优先搜素的思想，首先我们需要回顾一下树的遍历。二叉树中，前序遍历的代码如下：

class TreeNode{int val;TreeNode left;TreeNode right;
}
void treeDFS(TreeNode root) {if (root == null)return;System.out.println(root.val);treeDFS(root.left);treeDFS(root.right);  
}

如果是n叉树，就会变成：

class TreeNode{int val;List<TreeNode> nodes;
}
public static void treeDFS(TreeNode root) {//递归必须要有终止条件if (root == null){return;}//处理节点System.out.println(root.val);//通过循环，分别遍历N个子树for (int i = 1; i <= nodes.length; i++) {treeDFS("第i个子节点");}
}

因为是n叉树，所以没办法再用left和right表示分支了，这里用了一个List。观察上面的代码是不是和回溯的模板特别像！

暴力枚举解决不了的原因

看一下这道题，LeetCode 77：给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。你可以按 任何顺序 返回答案。

示例 ：

• 输入：n = 4, k = 2
• 输出：
  [
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
  ]

从4个数中选择2个:

• 先取1，则有[1,2]，[1,3]，[1,4]。
• 然后取2，因为1已经取过了，不再取，则有[2,3]，[2,4]。
• 再取一个3，因为1和2都取过了，不再取，则有[3,4]。
• 再取4，因为1，2，3都已经取过了，直接返回null。
• 所以最终是[1,2]，[1,3]，[1,4]，[2,3]，[2,4]，[3,4]。

写成代码双层循环轻松搞定:

int n = 4;
for (int i = 1; i <= n; i++) {for (int j = i + 1; j <= n; j++) {System.out.println(i + " " + j);}
}

但是如果n和k变得很大呢？取2个用2个循环，取k个要套多少层循环？显然暴力枚举就不行了，这就是组合问题。

回溯=递归+局部枚举+放下前任

继续以LeetCode 77为例子，图示枚举n=4，k=2的情况：

• 从第一层到第二层的分支有四个，分别表示可以取1，2，3，4。
• 从左向右取数，取过的数，不在重复取。
• 第一次取1，集合变为2，3，4 ，因为k为2，我们只需要再取一个数就可以了，分别取2，3，4，得到集合[1,2] [1,3] [1,4]。

以此类推：

n=5，k=3的情况：

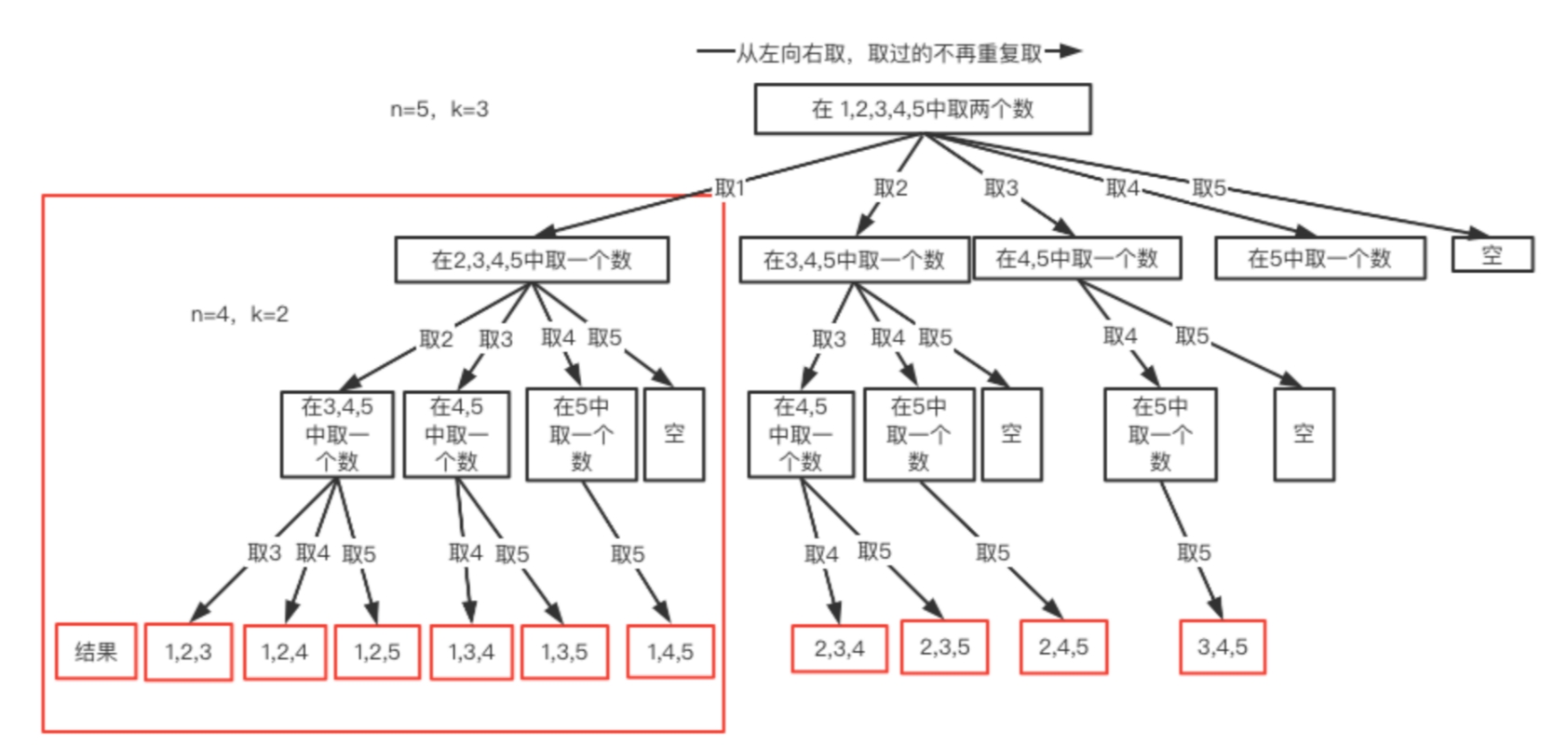
分析规律

图中每次访问到一次叶子节点(红框标记处)，就找到一个结果。虽然最后一个是空，但是不影响结果。这相当于只需要把从根节点开始每次选择的内容（分支）达到叶子节点时，将其收集起来就是想要的结果。

元素个数n相当于树的宽度（横向），k相当于树的深度（纵向）。所以我们说回溯算法就是一纵一横而已。再分析，我们还发现几个规律：

• 我们每次选择都是从类似{1,2,3,4}，{1,2,3,4,5}这样的序列中一个个选的，这就是局部枚举，而且越往后枚举范围越小。
• 枚举时，我们就是简单的暴力测试而已，一个个验证，能否满足要求，从上图可以看到，这就是N叉树遍历的过程，因此两者代码也必然很像。
• 我们再看上图中红色大框起来的部分，这个部分的执行过程与n=4，k=2的处理过程完全一致，很明显这是个可以递归的子结构。

为什么要手动撤销（放下前任）

收集每个结果不是针对叶子结点的，而是针对树枝的，比如最上层我们首先选了1，下层如果选2，结果就是{1,2}，如果下层选了3，结果就是{1,3}，依次类推。

观察图片，我可以在得到{1,2}之后将2撤掉，再继续取3，这样就得到了{1,3}，同理可以得到{1,4}，之后当前层就没有了，我们可以将1撤销，继续从最上层取2继续进行。

手动撤销对应的代码操作：

先将第一个结果放在临时列表path里，得到第一个结果{1,2}之后就将path里的内容放进结果列表resultList中，之后，将path里的2撤销掉， 继续寻找下一个结果{1.3},然后继续将path放入resultLit，然后再撤销继续找。

完整代码：

public List<List<Integer>> combine(int n, int k) {List<List<Integer>> resultList = new ArrayList<>();if (k <= 0 || n < k) {return resultList;}//用户返回结果Deque<Integer> path = new ArrayDeque<>();dfs(n, k, 1, path, res);return res;
}public void dfs(int n, int k, int startIndex, Deque<Integer> path, List<List<Integer>> resultList) {//递归终止条件是：path 的长度等于 kif (path.size() == k) {resultList.add(new ArrayList<>(path));return;}//针对一个结点，遍历可能的搜索起点，其实就是枚举for (int i = startIndex; i <= n; i++) {//向路径变量里添加一个数，就是上图中的一个树枝的值path.addLast(i);//搜索起点要加1是为了缩小范围，下一轮递归做准备，因为不允许出现重复的元素dfs(n, k, i + 1, path, resultList);//递归之后需要做相同操作的逆向操作,具体后面继续解释path.removeLast();}
}

热身小题

输出二叉树的所有路径

LeetCode 257：给你一个二叉树的根节点 root ，按任意顺序，返回所有从根节点到叶子节点的路径。

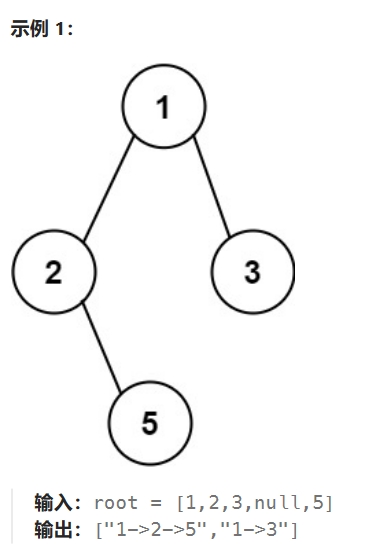
分析：可以得出有几个叶子结点就有几条路径。深度优先搜索就是从根节点开始一直找到叶子结点，我们这里可以先判断当前节点是不是叶子结点，再决定是不是向下走，如果是叶子结点，我们就增加一条路径。

从回溯的角度来看得到第一条路径125之后怎么找到第二条路径13，这里很明显就是先将5撤掉，发现还是不行，再撤掉2，然后接着递归就可以了。

class Solution {List<String> ans = new ArrayList<>();public List<String> binaryTreePaths(TreeNode root) {dfs(root,new ArrayList<>());return ans;}private void dfs(TreeNode root,List<Integer> temp){if(root == null){return ;}temp.add(root.val);//如果是叶子结点记录结果if(root.left == null && root.right == null){ans.add(getPathString(temp));}dfs(root.left,temp);dfs(root.right,temp);temp.remove(temp.size()-1);}//拼接结果private String getPathString(List<Integer> temp){StringBuilder sb = new StringBuilder();sb.append(temp.get(0));for(int i = 1;i < temp.size();++i){sb.append("->").append(temp.get(i));}return sb.toString();}
}

这是力扣上的简单题，怎么说呢？不知道大家做这道题怎么样，反正我是真的一点也没破防😎。

路径总和的问题

LeetCode 113：给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

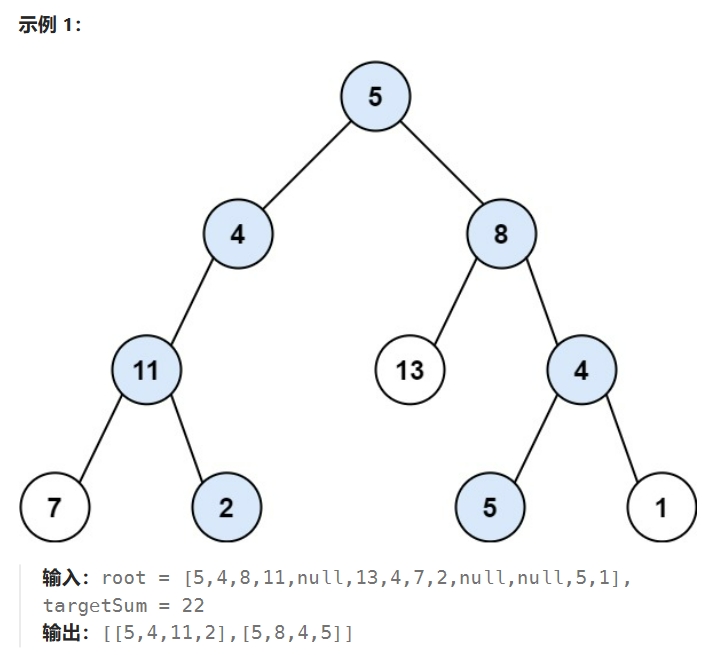
分析：我们发现根节点是5，因此只要从左侧或者右侧找到targetSum是17的即可。

• 看左子树，根值为4，那只要从node(4)的左右子树中找targetSum是13
• node(11)时，我们需要再找和为2的子链路，显然此时node(7)已经超了，要将node(7)给移除掉，继续访问node(2)。左子树遍历完毕
• 看根结点的右子树，要找targetSum为17的链路，方式与上面的一致。完整代码就是：

List<List<Integer>> res = new ArrayList<>();
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {LinkedList<Integer> path = new LinkedList<>();dfs(root,targetSum,path);return res;
}
public void dfs(TreeNode root,int targetSum,LinkedList<Integer> path){if(root == null){return ;}targetSum -= root.val;path.add(root.val);if(targetSum == 0 && root.left == null && root.right == null){res.add(new LinkedList(path));}dfs(root.left,targetSum,path);dfs(root.right,targetSum,path);path.removeLast();
}

总的来说：

1. 首先，我们传入一个二叉树的根节点和一个目标和。我们创建一个二维列表 res 用于保存结果。
2. 接着，我们创建一个 LinkedList 类型的 path 用于保存当前路径。使用深度优先搜索（DFS）的方式遍历二叉树，具体实现在 dfs 函数中。在 dfs 函数中，首先我们判断当前节点是否为空。如果为空，则直接返回。
3. 然后，我们将目标和减去当前节点值，并将当前节点的值添加到路径中。
4. 进一步，我们判断是否满足目标和为 0 且当前节点为叶子节点（即没有左右子树）。如果满足条件，我们将当前路径添加到结果列表 res 中。
5. 接下来，我们分别递归地遍历当前节点的左子树和右子树，注意此时目标和和路径都已经更新。
6. 最后，我们移除路径中的最后一个值，以便继续向上寻找其他路径。
7. 最终返回保存有所有符合条件路径的结果列表 res。

END

啊~~知识的力量，🧠脑子好疼🥲。下一篇我将专门介绍回溯思想的经典算法题目和应用场景，这篇就当是个入门，知道什么是回溯就行了。