抑制过拟合——Dropout原理
- Dropout的工作原理
- 实验观察
在机器学习领域,尤其是当我们处理复杂的模型和有限的训练样本时,一个常见的问题是过拟合。简而言之,过拟合发生在模型对训练数据学得太好,以至于它捕捉到了数据中的噪声和误差,而不仅仅是底层模式。具体来说,这在神经网络训练中尤为常见,表现为在训练数据上表现优异(例如损失函数值很小,预测准确率高)而在未见过的数据(测试集)上表现不佳。
过拟合不仅是机器学习新手容易遇到的问题,即使是经验丰富的从业者也会面临这一挑战。一个典型的解决方案是采用模型集成技术,这涉及训练多个模型并将它们的预测结合起来。但这种方法的缺点是显而易见的:它既耗时又昂贵,不仅在训练阶段,而且在模型评估和部署时也是如此。
在这种背景下,Dropout 作为一种有效的正则化技术,可以显著减轻过拟合问题。它的基本原理是在每次训练迭代中随机“丢弃”(即暂时移除)网络中的一部分神经元。这种方法不仅简单,而且被证明在许多情况下都非常有效。
Dropout的工作原理
在 PyTorch 中,Dropout 层的使用相当直观。通常,它被添加到神经网络的各个层之间,如下所示:
torch.nn.Dropout(p=0.5, inplace=False)
p:这是一个关键参数,代表着每个神经元被丢弃的概率。
在实践中,这意味着对于网络中的每个神经元,它在每次训练迭代中都有 1 − p 1-p 1−p 的概率被保留, p p p 的概率被丢弃。值得注意的是,这种随机性确保了每个mini-batch都在对不完全相同的网络进行训练,从而减少过拟合的风险。
在训练期间,对于每个训练样本,网络中的每个神经元都有概率 1 − p 1-p 1−p 被保留,概率 p p p 被丢弃。如果神经元被保留,则其输出乘以 1 1 − p \frac{1}{1-p} 1−p1(这样做是为了保持该层输出的总期望值不变)。设 r j r_j rj 为一个随机变量,它对应于第 j j j 个神经元,且服从伯努利分布(即 r j = 1 r_j = 1 rj=1 的概率为 1 − p 1-p 1−p, r j = 0 r_j = 0 rj=0 的概率为 p p p)。那么在训练时,神经元的输出 y j y_j yj变为 r j × y j / ( 1 − p ) r_j \times y_j / (1-p) rj×yj/(1−p)。
为什么需要保持期望不变? 举个简单的例子,假设某层有两个神经元,它们的输出在没有dropout时都是1。在应用了50%的dropout后,期望只有一个神经元被激活,输出为1,另一个被丢弃,输出为0。这样,这层的平均输出变成了0.5。为了保持输出的总期望值不变,激活的神经元的输出应该乘以2,即 1 1 − p \frac{1}{1-p} 1−p1,这样平均输出才能保持为1,与没有应用dropout时相同。这样的处理有助于保持整个网络的稳定性和一致性。
在模型预测(或测试)阶段,所有的神经元都保持激活(即不进行dropout)。因为在训练阶段,神经元的输出已经被放大了 1 1 − p \frac{1}{1-p} 1−p1 倍,所以在预测时不需要进行任何调整,直接使用网络进行前向传播即可。

实验观察
为了更深入地理解 Dropout 的影响,我们可以通过一个实验来观察不同的 Dropout 设置对训练过程的影响。比如,可以比较 Dropout = 0.1 和 Dropout = 0 在训练过程中的表现差异,相关代码实现如下:
import torch
from tensorboardX import SummaryWriter
from torch import optim, nn
import timeclass Model(torch.nn.Module):def __init__(self):super(Model, self).__init__()self.linears = nn.Sequential(nn.Linear(2, 20),nn.Linear(20, 20),nn.Dropout(0.1),nn.Linear(20, 20),nn.Linear(20, 20),nn.Linear(20, 1),)def forward(self, x):_ = self.linears(x)return _lr = 0.01
iteration = 1000x1 = torch.arange(-10, 10).float()
x2 = torch.arange(0, 20).float()
x = torch.cat((x1.unsqueeze(1), x2.unsqueeze(1)), dim=1)
y = 2*x1 - x2**2 + 1model = Model()
optimizer = optim.Adam(model.parameters(), lr=lr, weight_decay=0.01)
loss_function = torch.nn.MSELoss()start_time = time.time()
writer = SummaryWriter(comment='_随机失活')for iter in range(iteration):y_pred = model(x)loss = loss_function(y, y_pred.squeeze())loss.backward()for name, layer in model.named_parameters():writer.add_histogram(name + '_grad', layer.grad, iter)writer.add_histogram(name + '_data', layer, iter)writer.add_scalar('loss', loss, iter)optimizer.step()optimizer.zero_grad()if iter % 50 == 0:print("iter: ", iter)print("Time: ", time.time() - start_time)
这里我们使用 TensorBoardX 进行结果的可视化展示。
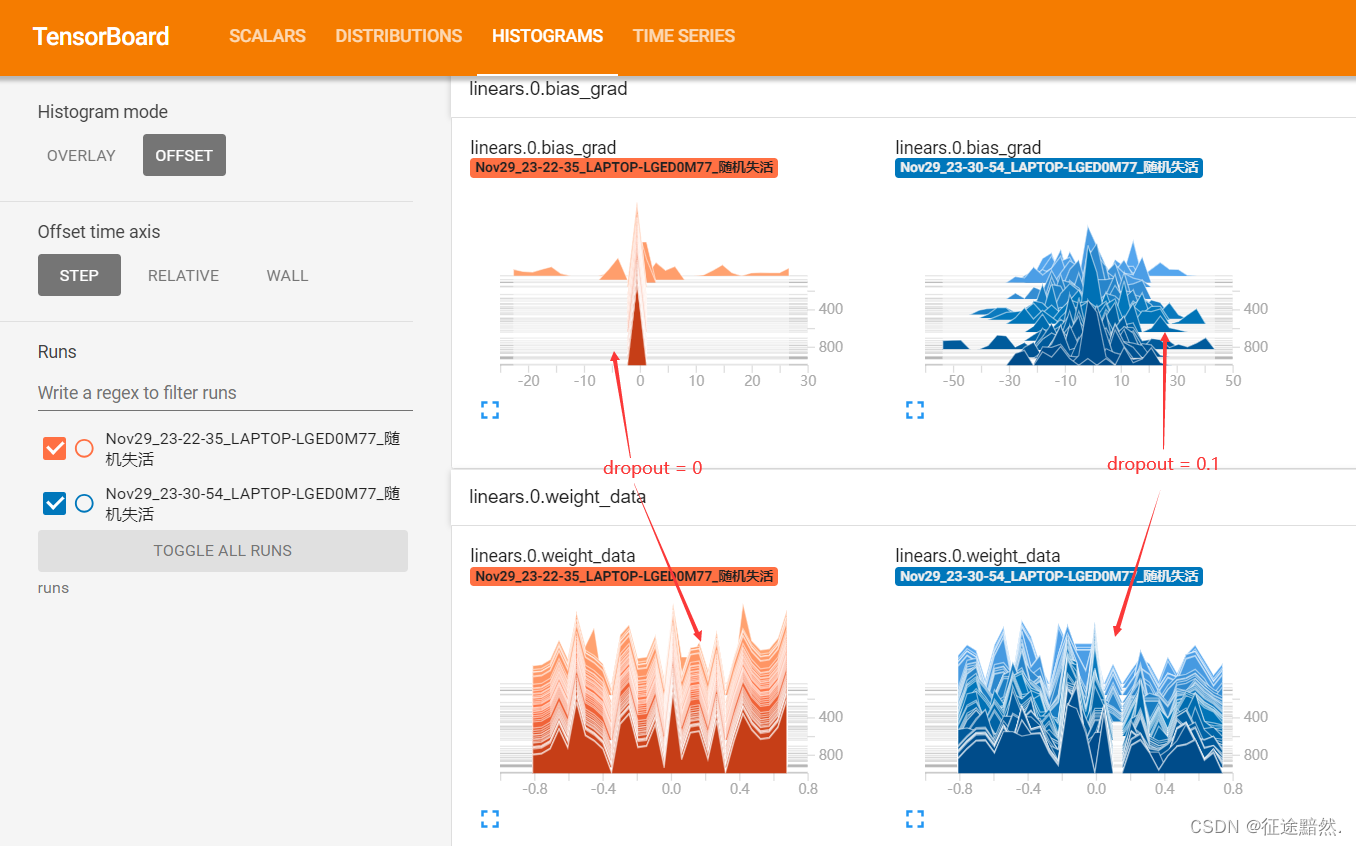
通过观察模型训练1000轮后的线性层梯度分布,可以发现,应用 Dropout 后的模型梯度通常会更加分散和多样化。这种梯度的多样性有助于防止模型过于依赖训练数据中的特定模式,从而减轻过拟合。
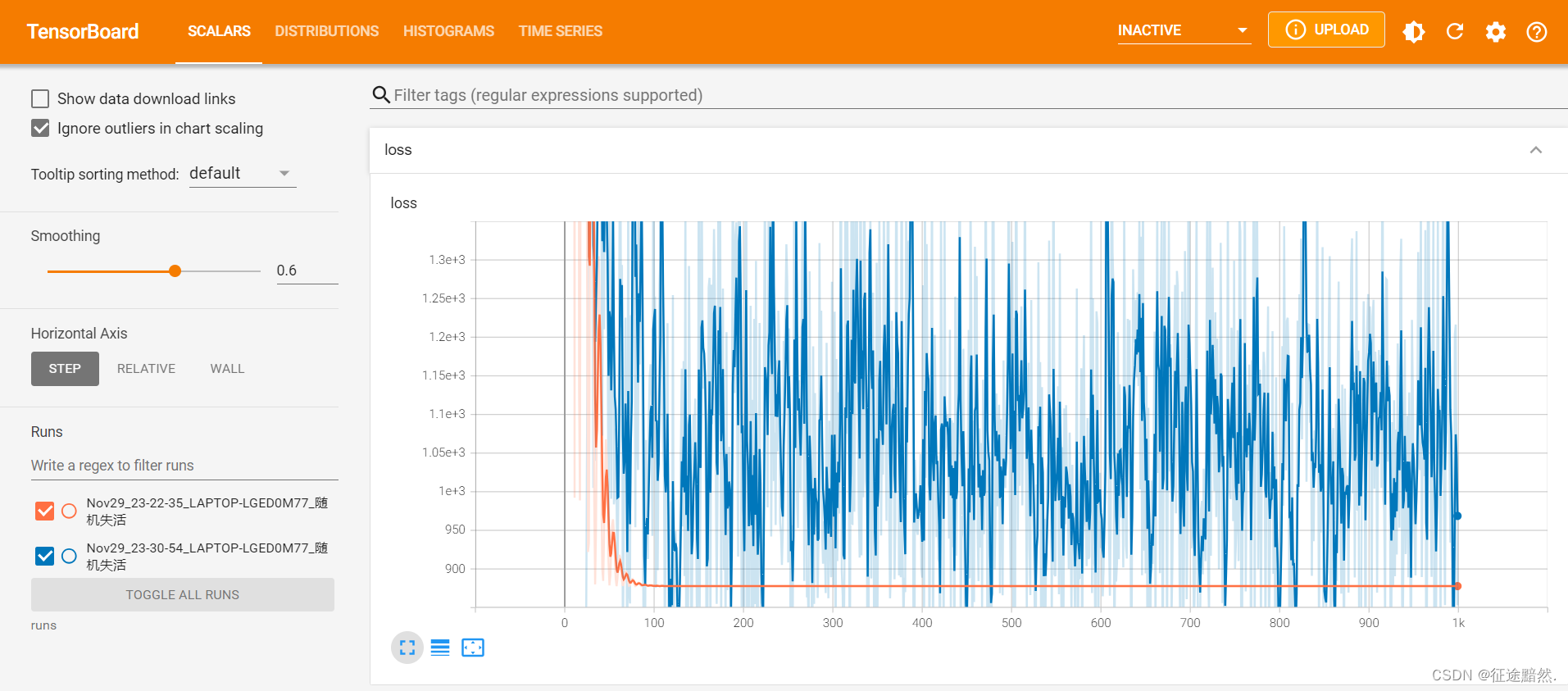
同样值得注意的是,模型的损失曲线也会受到影响。加入 Dropout 通常会使损失曲线出现更多的波动(例如,图中的蓝色曲线),这反映了模型在学习过程中的不稳定性。然而,这种不稳定性通常是可接受的,因为它反映了模型正在学习更多的泛化模式而不是简单地记住训练数据。


![[NOIP2016 普及组] 回文日期](https://img-blog.csdnimg.cn/direct/c0495f9f05004418816f008697a54536.png)