前言
先想策略, 然后分配时间, 做题的时候心态要好
主要问题还是怎么才能把做题能力练上去, 不好评价
看题
首先因为是 \(\rm{B}\) 组 , 所以很蓝的啦
\(\rm{T1}\)
性质题, 一眼没啥思路
\(\rm{T2}\)
不好, 是逆序对
\(\rm{T3}\)
困难
\(\rm{T4}\)
也许是树形 \(\rm{dp}\)
每道题 \(35 \ \rm{min}\) , 心态一定要好
打不出来就当暴力仙人, 总能拼上去的
\(\rm{T1}\)
刚看完题就听到有人开始敲键盘了, 害怕
思路
转化题意
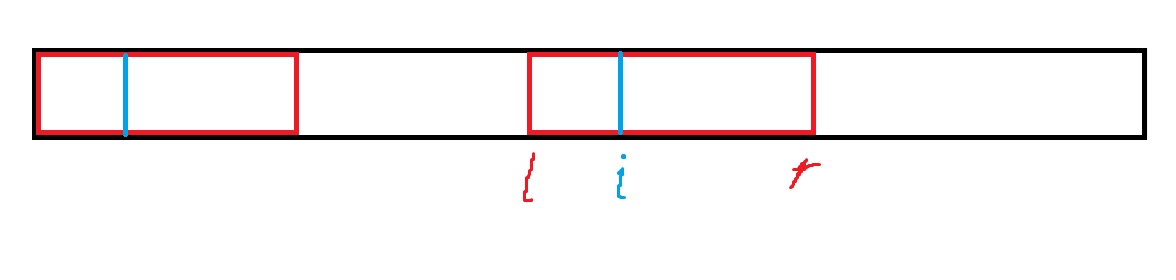
求最小的 \(K\) , 记 \(A[1 : K]\) 为 \(S\) , 记 \(A[k + 1 : 2K]\) 为 \(T\) , 使得存在一个 \(S, T\) 的映射关系对 \((S_i, T_j)\) , 使得每个关系对满足 \(S_i < T_j\)
本来想看下样例发现输入格式给反了???
首先观察到一个性质, 如果 \(S, T\) 存在合法映射, 那么把 \(S, T\) 排序后, 一定满足 \(S_i < T_i\)
观察大样例
46 47 17 26 38 52 11 29 42 18 36 31 2 7 33
25 58 28 32 19 39 19 43 7 55 55 58 46 8 33
对其排序
2 7 11 17 18 26 29 31 33 36 38 42 46 47 52
7 8 19 19 25 28 32 33 39 43 46 55 55 58 58
看上去的确满足这个性质
所以 \(\mathcal{O} (n^2 \log n)\) 的做法就有了 (然后这个时候 \(\rm{yhj}\) 给我说他会了, 上压力>_<)
怎么做?
你发现值域很小并且给出这个条件完全没有被利用
考虑对值域处理
如果用值域数组处理, 那么显然可以把 \(\mathcal{O} (n^2 \log n)\) 变成 \(\mathcal{O} (n (n + m))\)
考虑在这个基础上优化, 每次值域数组的变化是简单的, 稍微优化就是 \(\mathcal{O} (nm)\)
实现
框架
首先枚举 \(K\) , 每次移动 \(K\) 就对表示两个部分的值域数组维护, 这是 \(\mathcal{O} (1)\) 的, 然后对值域数组扫一遍即可, \(\mathcal{O} (m)\)
复杂度 \(\mathcal{O} (nm)\)
代码
#include <bits/stdc++.h>
#define int long long
const int MAXN = 2e4 + 20;
const int MAXVAL = 1e3 + 20;// #define testcaseint n, m;
int chest[MAXN];int val1[MAXVAL], val2[MAXVAL]; // 两个部分的值域数组
int ans = 0;int cval1[MAXVAL], cval2[MAXVAL];
/*两个值域数组的合法性*/
bool check() {for (int i = 1; i <= m; i++) cval1[i] = val1[i], cval2[i] = val2[i];int pointer = 0;for (int i = 1; i <= m; i++) {if (!cval1[i]) continue;while (pointer <= i) pointer++;while (cval1[i] && pointer <= m) {if (cval1[i] >= cval2[pointer]) cval1[i] -= cval2[pointer], cval2[pointer++] = 0;else cval2[pointer] -= cval1[i], cval1[i] = 0;}}for (int i = 1; i <= m; i++) if (cval2[i]) return false;return true;
}signed main()
{
#ifdef testcasefreopen("binstest.in", "r", stdin);freopen("myans.out", "w", stdout);
#endifscanf("%lld %lld", &m, &n);for (int i = 1; i <= n; i++) scanf("%lld", &chest[i]);for (int K = 1; K <= n / 2; K++) {/*维护值域数组*/ if (K != 1) val1[chest[K]]++, val2[chest[K]]--, val2[chest[2 * K]]++, val2[chest[2 * K - 1]]++;else val1[chest[K]]++, val2[chest[2 * K]]++;/*处理合法性*/if (check()) ans = std::max(ans, K);}printf("%lld", ans);return 0;
}
测了一下极端数据挺快的, 看着没啥问题, 不打拍子了
\(\rm{T2}\)
\(\rm{T1}\) 如果是这么做的, 显然是大众分的一部分, 如果我打的就是正解那么难度不超过 \(\textrm{div 2 C}\)
所以区分度还在这题, 加油
思路
看到大数据读入原地睡觉
至少段数应该是整数\(()\)
至少读入部分马蜂美丽\(()\)
转化题意
\(m\) 次操作, 每次把一个长为 \(2^n\) 的串均分成 \(2^{n - q_i}\) 个连续的长度为 \(2^{q_i}\) 长度的串, 将每个串翻转, 求最终逆序对的数量
看到逆序对就不会做 , 还有一道关于这个的题没复习完全, 寒假加油!
\(m = 0\) 的部分分是啥啊, 输出 \(0\) 吗?
那么 \(n \leq 5\) 好像是给暴力模拟的, 但是我不会归并排序求逆序对, 树状数组不能用啊
补好要被区分了
发现一个性质, 每次翻转, 串串之间的逆序对个数不会变, 只有串内的逆序对个数受到了影响
形象的, 不妨假设原串中的逆序对个数为 \(\omega\) , 记每个串中的逆序对个数为 \(w_i\) , 其大小为 \(s_i\)
那么反转之后这个串中的逆序对个数为 \(\displaystyle \frac{s_i \times (s_{i} - 1)}{2} - w_i\)
最终全串的逆序对个数即为 \(\displaystyle\omega - \sum_{i = 1}^{2^{n - q_i}} \frac{s_i \times (s_{i} - 1)}{2} - w_i\)
\(s_i = 2^{q_i}\) , 考虑怎么处理 \(w_i\) , 先出去上个厕所冷静一下
好的没上出来, 多喝水
不管了, \(q_i\) 值域很小的情况下, 我们可以考虑直接预处理原串中, 对于所有 \(s_i\) 的 \(w_i\) , 这个可以通过类似 \(\textrm{ST}\) 表的倍增过程搞出来, 每次翻转实际上就是翻转一整个区间
感觉这样捋不明白, 你发现现在的长度为 \(2^{q_i}\) 的串给人一种直觉, 放到树上处理看行不行
容易发现构成了一颗完全满二叉树
每次操作, 相当于挑选了这颗树的一层, 对于之中的点进行翻转, 这个感觉可以通过 \(\textrm{lazy tag}\) 实现实时处理每个节点的 \(ls, rs\)
那么怎么求答案, 还是和上面一样, 我们要维护每一段 \((\)树上每一点\()\) 中的逆序对个数
发现困难在于合并一个节点的两个子节点的性质, 逆序对太难维护了
考虑在每个点树套树维护一个值域线段树, 显然糖到爆炸, 还要线段树合并这种神经操作 \((\)不会正解真的这样啊吧\()\)
不过好像可以先预处理出每个节点的左右儿子对应的区间合并起来之后逆序对的数量, 先去把后面想了再继续想这道题
然后就是逆序对可以只由大小关系推得, 显然可以处理成离散化的形式
实现
框架
\(m = 0\) , 直接输出 \(0\)
首先, 对原串进行离散化, 然后再暴力处理每次询问的影响, 然后直接暴力统计逆序对个数
代码
#include <bits/stdc++.h>
#define int long long
const int MAXN = 40;int n, m;
int a[MAXN], q[1000020];typedef unsigned long long ull;
namespace IO {ull read() {ull x = 0; char ch = getchar();while (ch > '9' || ch < '0') ch = getchar();while (ch >= '0' && ch <= '9') x = x * 10 + (ch - '0'), ch = getchar();return x;}
} using namespace IO;#define lowbit(x) ((x) & (-x));
class BIT
{
private:int tree[MAXN << 1]; // 保险一点public:/*初始化*/ void init() { memset(tree, 0, sizeof tree); }/*单点修改*/ void update(int x, int d) { while (x <= n) tree[x] += d, x += lowbit(x); }/*前缀最大值*/ int query(int x) { int ans = 0; while (x > 0) ans += tree[x], x -= lowbit(x); return ans; }
} bit;ull k1, k2, threshold;
ull xorShift128Plus() {ull k3 = k1, k4 = k2;k1 = k4;k3 ^= (k3 << 23);k2 = k3 ^ k4 ^ (k3 >> 17) ^ (k4 >> 26);return k2 + k4;
}
void gen(int n, int m, int threshold, ull _k1, ull _k2) {k1 = _k1, k2 =_k2;for (int i = 1; i <= (1 << n); i++) a[i] = xorShift128Plus() % threshold + 1;for (int i = 1; i <= m; i++) q[i] = xorShift128Plus() % (n + 1);
}int bin[MAXN];
/*离散化*/
void lhs() {for (int i = 1; i <= (1 << n); i++) bin[i] = a[i];std::sort(bin + 1, bin + (1 << n) + 1);int cnt = std::unique(bin + 1, bin + (1 << n) + 1) - (bin + 1);for (int i = 1; i <= (1 << n); i++) a[i] = std::lower_bound(bin + 1, bin + cnt + 1, a[i]) - bin;
}int ans[1000020];
int res = 0;signed main()
{scanf("%lld %lld %lld", &n, &m, &threshold);k1 = read(), k2 = read();gen(n, m, threshold, k1, k2);if (m == 0) { printf("0"); exit(0); }lhs();for (int cas = 1; cas <= m; cas++) {/*处理翻转*/for (int i = 1; i <= (1 << (n - q[cas])); i++) {int L = (i - 1) * (1 << q[cas]) + 1, R = i * (1 << q[cas]);std::reverse(a + L, a + R + 1);}bit.init();for (int i = (1 << n); i >= 1; i--) {ans[cas] += bit.query(a[i] - 1);bit.update(a[i], 1);}}for (int cas = 1; cas <= m; cas++) res ^= (ans[cas] * cas);printf("%lld", res);return 0;
}
\(\rm{T3}\)
先把后面暴力什么的能拿的拿了, 然后把 \(\rm{T2}\) 暴力打了
思路
首先考虑对于一个串, 怎么计算其可能提供的选项种数
这个显然是可行性 \(\rm{dp}\) 秒了类型的题目
所以 \(\mathcal{O} (N^2 val)\) 秒了
不对秒不掉
首先我们考虑枚举 \(P\) \(\mathcal{O} (n)\) , 然后我们处理其他位置的可行性 \(\rm{dp}\) \(\mathcal{O} (n)\) , 然后最后考虑 \(Q\) 是 \(\mathcal{O} (\sum \upsilon)\) 的, 其中 \(\upsilon\) 是值域
形象的转化问题, 我们要求出对于一个集合 \(\mathbb{S}\) , 使得 \(\mathbb{S} \cup (\mathbb{S} \to k) = \varnothing\) 的最小 \(k\) , 时间复杂度要求 \(\mathcal{O} (n)\)
想了一下没啥思路, 但是你直接枚举 \(k\) 可以做到 \(\mathcal{O} (n^2 \sum \upsilon)\) , 可以通过暴力的 \(30 \%\)
实现
框架
如上处理即可, 可以 \(\rm{bitset}\)
代码
#include <bits/stdc++.h>
#define int long long
const int MAXN = 21;int n;
int num[MAXN];
int sum;struct node { int P, Q, ans; } ans;signed main()
{scanf("%lld", &n);for (int i = 1; i <= n; i++) scanf("%lld", &num[i]), sum += num[i];for (int P = 1; P <= n; P++) { // 外层枚举 P/*首先处理其他位置的可行性 dp*/std::bitset<280020> dp;dp.reset();for (int i = 1; i <= n; i++) {if (i == P) continue;dp = dp | (dp << num[i]);dp[num[i]] = 1;}/*然后枚举 k , 检查*/int k;std::bitset<280020> ret;for (k = 0; k <= sum + 1; k++) {ret.reset();ret = dp | (dp << k); ret[k] = 1;if (ret.count() == dp.count() * 2 + 1) break;}if (ans.ans < ret.count()) ans = {num[P], k, (long long)(ret.count())};else if (ans.ans == ret.count()) {if (ans.P > num[P]) ans = {num[P], k, (long long)(ret.count())};else if (ans.P == num[P]) {if (ans.Q > k) ans = {num[P], k, (long long)(ret.count())};}}}printf("%lld %lld", ans.P, ans.Q);return 0;
}
总结
继续 \(\textrm{div 2 C}\) , 策略已经不错了
下午放寒假了, 爽