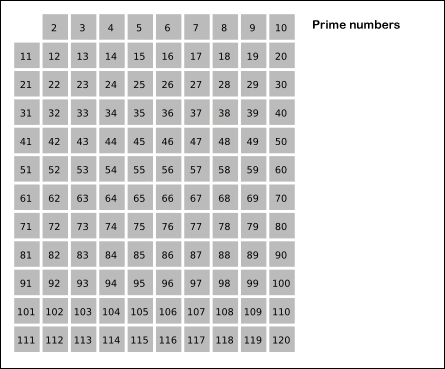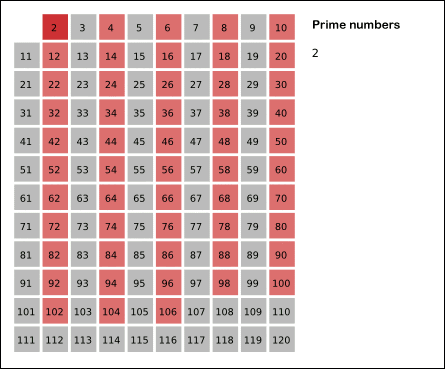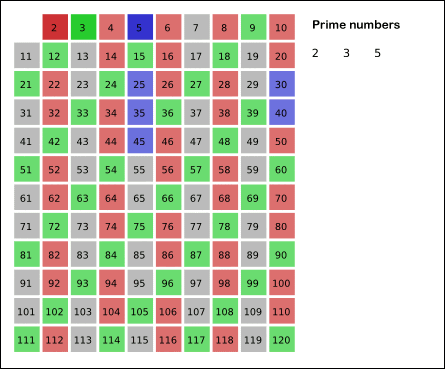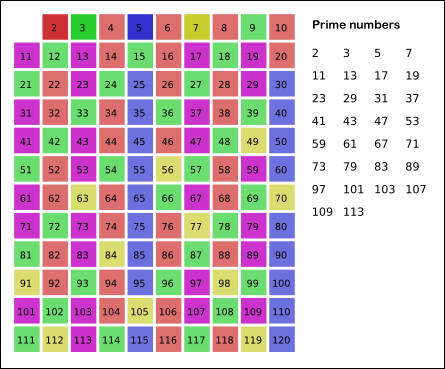
def is_prime(n):if n % 2 == 0 and n != 2:return Falsefor i in range(3, int(math.sqrt(n) + 1)):if n % i == 0:return Falsereturn n != 1def eratosthenes(n):primes = []is_prime = [True] * (n + 1)for i in range(2, n+1):if is_prime[i]:primes.append(i)# 用当前素数i去筛掉所有能被它整除的数for j in range(i * 2, n+1, i):is_prime[j] = Falsereturn primesdef ertosthenes(n):primes = []is_prime = [True] * (n+1)for i in range(2, n+1):if is_prime[i]:primes.append(i)for j, p in enumerate(primes):# 防止越界if p > n // i:break# 过滤is_prime[i * p] = False# 当i % p等于0的时候说明p就是i最小的质因数if i % p == 0:breakreturn primes再来个BING写的c++
#include<iostream>
#include<cstdio>
using namespace std;
const int maxn=5000000;
long prime[maxn]; // 存储一个个确定为质数的数
bool is_prime[maxn+1]; // 标记范围内所有数
int p = 0;
int sieve(int n) {p = 0;for(int i=0;i<=n;i++) is_prime[i]=true; // 所有数先标记为trueis_prime[0] = is_prime[1] = false; // 把数字0,1标记为质数for(int i=2;i<=n;i++) {if(is_prime[i]) // 如果这个数没有被标记为false{prime[p++]=i; // 用prime数组存起来这个数,既存起了质数,又用p表示了质数个数for(int j=i*i;j<=n;j+=i) // 这里没有优化时的写法是for (int j=2*i; j<=n; j++)。//因为小于j (即i^2)内的合数都因为 (根号j) (即i)内有更小的j的的因数而被排除// 比如3^2 = 9,为什么不算2*3 = 6呢, 因为6<9,所以6因为3以内有更小的因数而直接被排除is_prime[j]=false;}}return p; // 返回质数个数
}
int main() {//测试int n;while(~scanf("%d",&n)) {printf("质数个数是: %d\n",sieve(n));printf("质数有:\n");for (int i = 0; i<p; i++) {printf("%d ", prime[i]);printf("\n\n");}}system("pause");
}
is_prime[0] = is_prime[1] = false;
竟然符合c++语法...震惊.