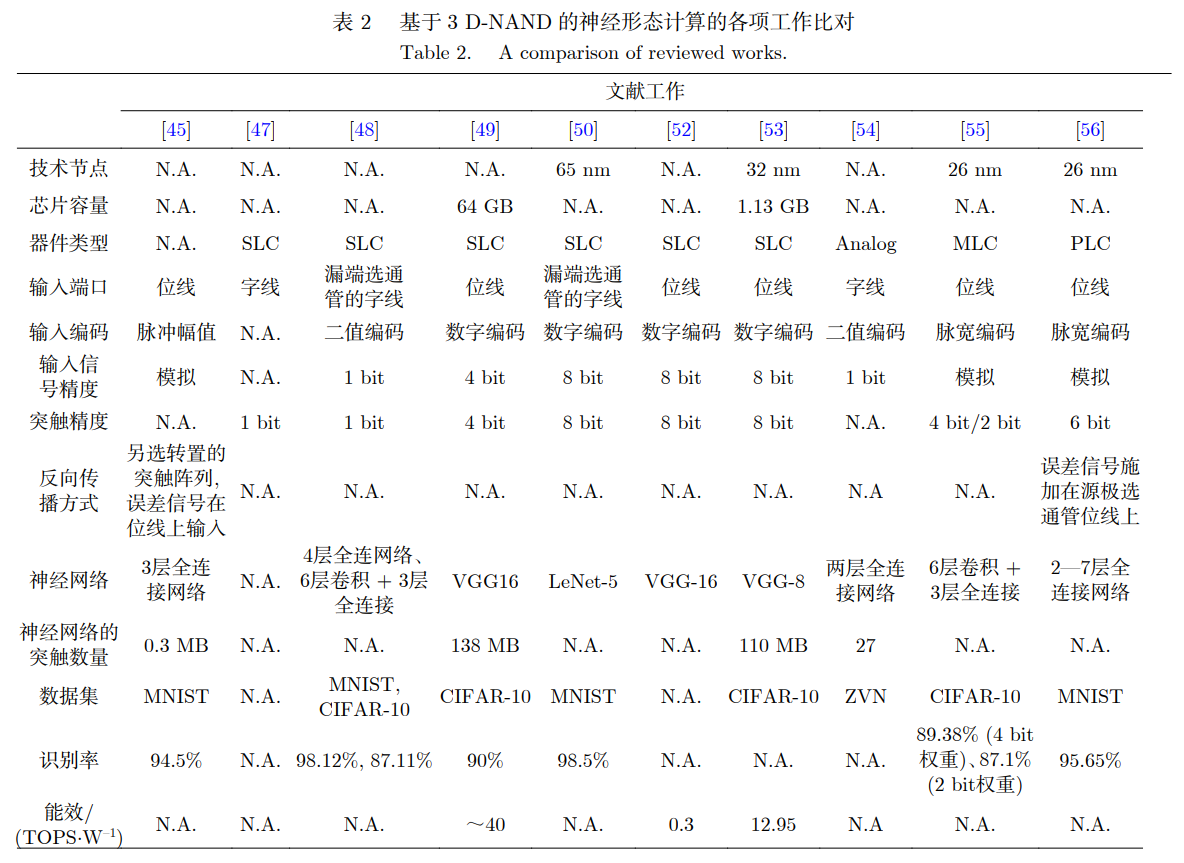
因为今天场上成功手搓三维 FWT 决定深刻背诵一下。
以下默认 \(\oplus\) 为高维不进位加法。
分圆多项式
手玩转移矩阵太过神秘了,不讨论了就。
定义分圆多项式 \(\Phi_k(x)=\prod_{\gcd(i,k)=1}(x-w_k^i)\)。
根据 \(x^i-1=\prod_{d|i}\Phi_d(x)\) 可以化简得到 \(\Phi_k(x)=\prod_{d|k}(x^d-1)^{\mu(\frac{k}{d})}\)。
分圆多项式是素多项式,在高维 FWT 中可以当成模数使用。
然后因为 \(\Phi_k(x)|x^k-1\),所以一般过程中模 \(x^k-1\),最后再模 \(\Phi_k(x)\)。
高维 FWT
以下只讨论 \(\oplus\)。
因为 FWT 是线性变换所以考虑构造变换矩阵:
其中 \(w_{j,i}w_{k,i}=w_{j\oplus k,i}\)。
然后这是范德蒙德矩阵,所以逆变换矩阵为:
模数良好时模意义下可能存在单位根 \(w_k\),但是有时可能不存在,所以考虑一种通解,去人为定义一个形式幂级数 \(x\),然后做模多项式运算。
一般这里的模数多项式取 \(\Phi_k(x)\),因为你取 \(x^k-1\) 为模数多项式时,他不是素的,所以可能存在多项式没有逆元,取 \(\Phi_k(x)\) 就没有这个问题。
关于复杂度,你正常 FWT 不看内层运算的复杂度是 \(O(mk^m)\),内层运算的复杂度是 \(O(k^2\times k)\) 的,所以总复杂度是 \(O(mk^{m+3})\)。
例题
CF1103E
就是求 \((\sum x^{a_i})^n\),高维 FWT 板子。
P5577
就是求 \(\prod_{i=1}^n(1+x^{a_i})\),因为 \(n\) 较大所以肯定不能暴力算,考虑研究一下 \(FWT(1+x^{a_i})\) 的性质。
不难发现 \(FWT_k(1+x^{a_i})=c_{1,k}+c_{a_i,k}=1+c_{a_i,k}\)。
那么 \(FWT_k(\prod_{i=1}^n(1+x^{a_i}))=\prod_{i=1}^nFWT_k(1+x^{a_i})=\prod_{i=1}^n(1+c_{a_i,k})\)。
所以说你现在只需要去计算 \(1+c_{a_i,k}\) 的指数,因为 \(c_{a_i,k}\) 只有 \(k\) 中取值,所以相当于要对每一位计算 \(1+w_k^n\) 的指数。
然后我们再考虑 \(FWT_k(\sum_{i=1}^nx^{a_i})=\sum_{i=1}^nFWT(x^{a_i})=\sum_{i=1}^nc_{a_i,k}\),也就是说直接对原序列的计数数组 FWT 得到结果的每一位的 \(w_k^n\) 的系数,就是你原始式子 \(1+w_k^n\) 的指数。
然后套板子就行。
ABC367G
求的是 \(\sum_{k=0}^Nk^K[x^ky^0]\prod_{i=1}^n(1+x^{a_i}y)\),\(x\) 做的是异或卷积,\(y\) 做的是长为 \(m\) 循环卷积。
先考虑求后面的 \(\prod_{i=1}^n(1+x^{a_i}y)\),发现这长得很像上一题,因为二位异或 FWT 的矩阵是 \(\begin{bmatrix}1&1\\1&-1\end{bmatrix}\),所以 \(FWT_k(\prod_{i=1}^n(1+x^{a_i}y))=\prod_{i=1}^nFWT_k(1+x^{a_i}y)=\prod_{i=1}^n(1\plusmn y)\)。
相当于你对每一位要算 \(1+y\) 的系数和 \(1-y\) 的指数,设这两个指数为 \(c_0,c_1\),根据上一题的结论我们有 \(c_0+c_1=n,c_0-c_1=FWT_k(\sum x^{a_i})\)。
然后求出 \([y^0](1+y)^{c_0}(1-y)^{c_1}\) 后再 IFWT 回去就是答案。