如果你曾经编写过或计划编写任何类型的图像处理代码,你应该完成以下测验。 如果你对一个或多个问题的回答是肯定的,那么你的代码很可能做错了事情并产生不正确的结果。 这对你来说可能不会立即显而易见,因为这些问题可能很微妙,并且在某些问题域中比在其他问题域中更容易发现。
NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎
有关Gamma(伽玛)的测验如下:
- 我不知道Gamma校正是什么。
- Gamma是 CRT 显示时代的遗物; 现在几乎每个人都使用液晶显示器,因此可以忽略它。
- Gamma仅与在印刷行业工作的图形专业人员相关,其中准确的色彩再现非常重要 - 对于一般图像处理,可以安全地忽略它。
- 我是一名游戏开发者,我不需要了解Gamma。
- 我的操作系统的图形库可以正确处理Gamma。
- 我正在使用的流行图形库 <在此插入名称> 可以正确处理伽玛。
- RGB 值为
(128, 128, 128)的像素发出的光大约是 RGB 值为(255, 255, 255)的像素的一半。 - 可以使用一些库将流行图像格式(JPEG、PNG、GIF 等)中的像素数据加载到缓冲区中,并直接对原始数据运行图像处理算法。
如果你的大部分回答都是“是”,请不要感到难过! 一周前,我自己也会对其中大部分问题做出肯定的回答。 不知何故,Gamma这个话题不在在大多数计算机用户的关注范围内(包括编写商业图形软件的程序员!),以至于当今的大多数图形库、图像查看器、照片编辑器和绘图软件仍然无法正确使用Gamma,并且 产生不正确的结果。
因此,请继续阅读,读完本文后,你将比绝大多数程序员更了解Gamma!
1、Gamma校正的神秘艺术
鉴于视觉可以说是人机交互最重要的感官输入通道,伽玛校正是程序员中谈论最少的主题之一,并且在技术文献(包括计算机图形文本)中很少提及,这非常令人惊讶。 事实上,大多数计算机图形学教科书都没有明确提到正确伽玛处理的重要性,或者以实际的方式讨论它,这根本没有帮助(我大学的 CG 教科书完全属于这一类,我刚刚检查过) 。 有些书以有些模糊和抽象的术语顺便提到了伽玛校正,但随后既没有提供如何正确执行伽玛校正的具体示例,也没有解释不正确执行伽玛校正的含义,也没有显示不正确伽玛处理的图像示例 。
在编写光线追踪器期间,我遇到了正确的Gamma处理的需要,我不得不承认我对这个主题的理解相当肤浅和不完整。 于是我花了几天时间在网上查了一下,结果发现很多关于gamma的文章也没什么帮助,因为很多都太抽象和混乱,有些包含了太多有趣但又不相关的细节,然后 其他一些缺乏图像示例,或者只是不正确或难以理解。 Gamma一开始并不是一个非常困难的概念,但由于某些神秘的原因,找到正确、完整并以清晰的语言解释该主题的文章并不容易。
2、什么是Gamma?为什么我们需要它?
好吧,我试图对伽玛进行全面的解释,只关注最重要的方面,并假设事先不了解它。
本文中的图像示例假设你正在计算机显示器(CRT 或 LCD,无所谓)上的现代浏览器中查看此网页。 与显示器相比,平板电脑和手机通常不太准确,因此请尽量避免使用这些设备。 你应该在光线昏暗的房间中观看图像,因此请不要在屏幕上直射灯光或耀斑。
2.1 发光与感知亮度
不管你相信与否,下图中任意两个相邻垂直条之间的光能发射差异是一个常数。 换句话说,从左到右,屏幕发出的光能量以恒定的量增加。

图 1:发射光强度均匀分布的灰度条
现在考虑下图:
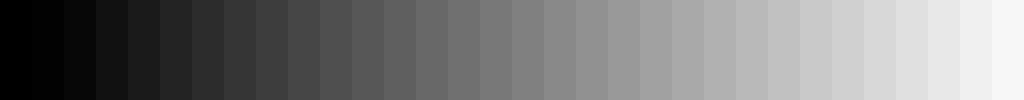
图 2:感知光强度的均匀分布的灰度条
哪张图像上的渐变显得更均匀? 是第二个! 但为什么会这样呢? 我们刚刚确定,在第一张图像中,条形在显示器能够再现的最暗黑色和最亮白色之间的发射光强度方面均匀(线性)间隔。 但为什么我们不认为这是一个从黑到白的均匀渐变呢? 我们认为是线性渐变的第二张图像上显示了什么?
答案在于人眼对光强度的响应,这是非线性的。 在第一个图像中,任何两个相邻条的标称光强度之间的差异是恒定的:
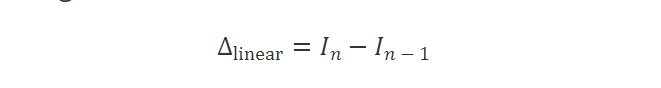
然而,在第二张图像上,这种差异并不是恒定的,而是随条形变化而变化;准确地说,它遵循幂律关系。 所有人类感官知觉在刺激幅度及其感知强度方面都遵循类似的幂律关系。
正因为如此,我们说标称物理光强度与感知亮度之间存在幂律关系。
2.2 物理线性与感知线性
假设我们想要将以下现实世界对象的表示形式存储为计算机上的图像文件(让我们假设现实世界中存在完美的灰度渐变,好吗?)以下是“现实世界对象”的外观:

图 3:理想的平滑灰度渐变
现在,假设我们只能在这个特定的计算机系统上存储 5 位灰度图像,这为我们提供了从绝对黑色到绝对白色的 32 种不同的灰色阴影。 此外,在这台计算机上,灰度值与其相应的物理光强度成正比,这将产生如图 1 所示的 32 元素灰度。我们可以说,该灰度在连续值之间的光发射方面是线性的。
如果我们仅使用这 32 个灰度值对平滑渐变进行编码,我们会得到类似的结果。为了简单起见,我们暂时忽略抖动:
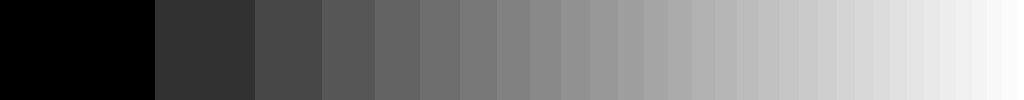
图 4:用 32 个物理线性灰度值表示的理想平滑灰度渐变
嗯,过渡相当突然,尤其是在左侧,因为我们只有 32 个灰度值可供使用。 如果我们稍微眯起眼睛,就很容易让自己相信,在我们有限的位深度允许的范围内,这或多或少是平滑梯度的“准确”表示。 但请注意左侧的台阶比右侧大得多 - 这是因为我们使用的灰度与发射的光强度呈线性关系,但正如我们之前提到的,我们的眼睛感知不到光强度 以线性方式!
这一观察有一些有趣的含义。 原始版本和 5 位编码版本之间的误差在整个图像中不均匀; 暗值比亮值大得多。 换句话说,我们正在失去深色值的表示精度,并且对于较浅的阴影使用相对过多的精度。 显然,我们最好为有限的色调调色板选择一组不同的 32 种灰色,这将使误差均匀分布在整个范围内,因此深色和浅色都将以相同的精度表示。 如果我们用这样的灰度对原始图像进行编码,该灰度在感知上是线性的,但因此在发射光强度方面是非线性的,并且该非线性将与人类视觉的非线性相匹配,我们将得到与我们完全相同的灰度图像。 在图2中已经看到:
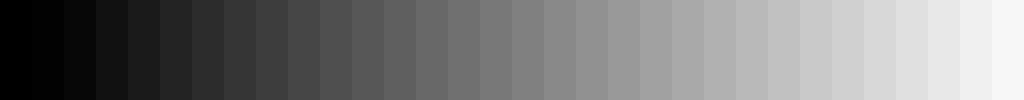
图 5:用 32 个感知线性灰度值表示的理想平滑灰度
我们这里讨论的非线性是之前提到的幂律关系,我们需要对物理线性灰度值进行非线性变换,将其转换为感知线性值,称为伽玛校正(gamma-correction)。
2.3 高效的图像编码
为什么上述所有内容都很重要? 所谓“真彩色”或“24 位”位图图像中的颜色数据每个像素存储为三个 8 位整数。 使用 8 位,可以表示 256 个不同的强度级别,如果这些级别的间距在物理上是线性的,我们将在深色阴影上失去很多精度,同时在浅色阴影上(相对而言)不必要地精确,如上所示。
显然,这并不理想。 一种解决方案是简单地继续使用物理线性标度并将每个通道的位深度增加到 16(或更多)。 这将使存储要求加倍(或更糟),而在发明大多数常见图像格式时,这不是一个选择。 因此,采取了不同的方法。 这个想法是让 256 个不同的级别代表感知线性尺度上的强度值,在这种情况下,绝大多数图像可以在每个颜色通道仅 8 位上充分表示。
用于表示通过算法综合生成的物理线性强度数据或由线性设备(例如数码相机或扫描仪的 CMOS)捕获的物理线性强度数据以及感知线性标度的离散值的变换称为伽玛编码。
几乎所有消费级电子设备上使用的 24 位 RGB 颜色模型 (RGB24) 均使用每个通道 8 位伽马编码值来表示光强度。 如果你还记得我们之前讨论过的内容,这意味着 RGB(128, 128, 128) 像素发出的光能不会是 RGB(255, 255, 255) 像素发出的光能的大约 50%,而只有 22% 左右! 这很有道理! 由于人类视觉的非线性特性,光源需要衰减至其原始光强度的 22% 左右,才能在人类看来亮度减半。 对于我们来说,RGB(128, 128, 128) 的亮度似乎是 RGB(255, 255, 255) 的一半! 如果你觉得这令人困惑,请反思一下,因为对到目前为止所讨论的内容有一个扎实的理解至关重要(相信我,这只会让你更加困惑)。
当然,伽玛编码始终是在假设图像最终要供人类在计算机屏幕上查看的情况下完成的。 在某种程度上,你可以将其视为有损 MP3,但用于图像压缩。 对于其他目的(例如,科学分析或用于进一步后处理的图像),使用浮点数并坚持使用线性比例通常是更好的选择,我们稍后会看到。
2.4 伽马传递函数
将值从线性空间转换到伽玛空间的过程称为伽玛编码(或伽玛压缩)和逆伽玛解码(或伽玛展开)。
这两个运算的公式非常简单,我们只需要使用前面提到的幂律函数即可:
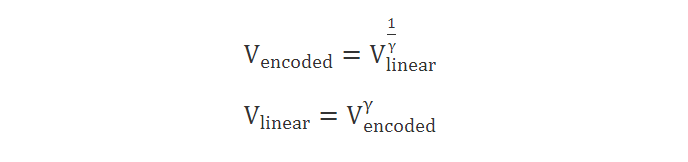
计算机显示系统中使用的标准伽马 (γ) 值为 2.2。 主要原因是 2.2 的伽玛值大约与人类视觉的幂律灵敏度相匹配。 应该使用的确切值因人而异,还取决于照明条件和其他因素,但必须选择一个标准值,2.2 就足够了。 别太在意这个。
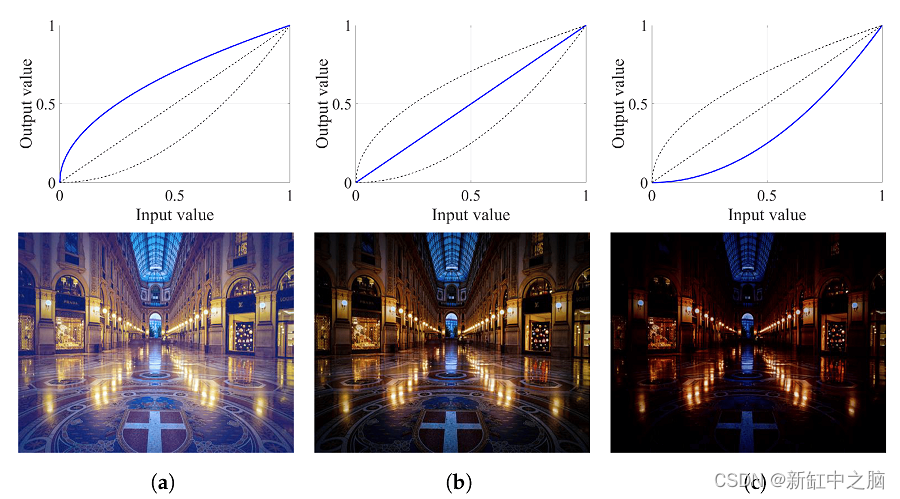
现在,许多文本都没有提到的一个非常重要的一点是,输入值必须在 0 到 1 范围内,并且输出也将映射到相同的范围。 由此得出一个稍微适得其反的事实:0 到 1 之间的伽玛值用于编码(压缩),大于 1 的伽玛值用于解码(展开)。 下图展示了用于编码和解码的伽玛传递函数,以及简单的线性伽玛(γ=1.0)情况:
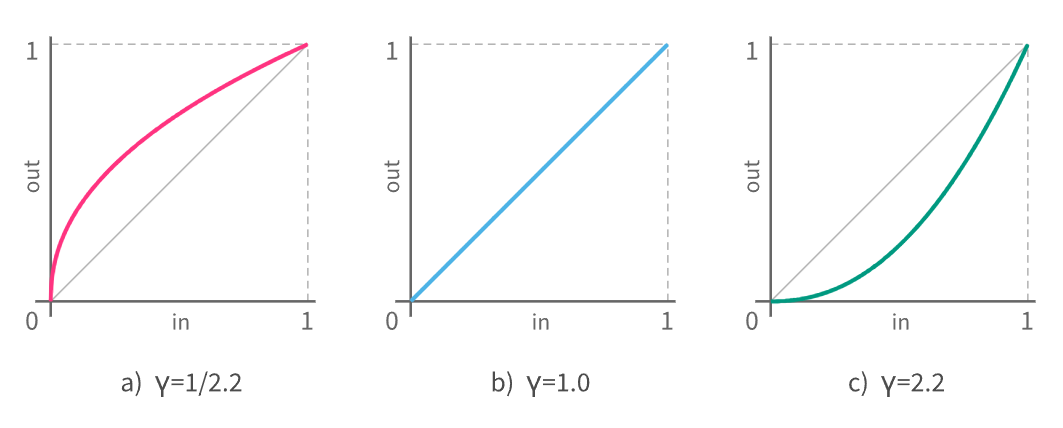
图 6:伽马传递函数 a)编码 b)线性 c)解码
到目前为止,我们只看到了灰度示例,但 RGB 图像没有什么特别之处,我们只需要使用相同的方法单独编码或解码每个颜色通道即可。
2.5 伽玛与 sRGB
sRGB 是一种色彩空间,是当今消费电子设备的事实上的标准,包括显示器、数码相机、扫描仪、打印机和手持设备。 它也是互联网上图像的标准色彩空间。
sRGB 规范定义了用于编码和解码 sRGB 图像的伽玛值(以及色域等其他内容,但这些与我们当前的讨论无关)。 sRGB gamma 非常接近标准 gamma 2.2,但它在非常暗的范围内有一个短的线性段,以避免零处的无穷大斜率(这在数值计算中更方便)。 可以在此处找到从线性到 sRGB 以及反向转换的公式。
你实际上并不需要了解所有这些更详细的细节。 需要了解的重要一点是,在 99% 的情况下,你会想要使用 sRGB 而不是普通伽玛。 原因是自 2005 年左右以来,所有显卡都具有硬件 sRGB 支持,因此大多数时候解码和编码实际上是免费的。 你的显示器的本机色彩空间很可能是 sRGB(除非它是用于图形、照片或视频工作的专业显示器),因此如果你只是将 sRGB 编码的像素数据放入帧缓冲区中,生成的图像在屏幕上看起来将是正确的(假设显示器已正确校准)。 流行的图像格式(例如 JPEG 和 PNG)可以存储色彩空间信息,但图像通常不包含此类数据,在这种情况下,几乎所有图像查看器和浏览器都会按照惯例将它们解释为 sRGB。
2.6 伽马校正
到目前为止我们已经讨论了gamma编码和解码,那么什么是gamma校准呢? 我也发现这有点令人困惑,所以让我来澄清一下。
如前所述,当今 99% 的显示器本身就使用 sRGB 色彩空间,但由于制造误差,大多数显示器将受益于一些额外的伽玛校准,以实现最佳效果。 现在,如果您从未校准过显示器,并不意味着它不会使用伽玛! 这根本不可能,过去和现在的大多数 CRT 和 LCD 显示器都是为了在 sRGB 下运行而设计和制造的。
将伽马校正视为微调。 你的显示器将始终以 sRGB 运行,但通过对其进行校准(在显卡驱动程序中或在操作系统级别),显示器的伽玛传输曲线将更接近我们之前讨论的理想伽玛传输函数。 此外,几年前,通过在图形管道(例如显卡、操作系统和应用程序级别)中应用多个伽马校正阶段,可能会以各种创造性的方式搬起石头砸自己的脚,但幸运的是,现在处理得更加智能。 例如,在我的 Windows 7 机器上,如果我在 NVIDIA 控制面板中打开伽玛校准,则操作系统级别校准将被禁用,反之亦然。
2.7 处理伽马编码图像
那么,如果几乎全世界都默认使用 sRGB,那么到底问题出在哪里呢? 如果我们的相机写入 sRGB JPEG 文件,我们只需解码 JPEG 数据,将其复制到显卡的帧缓冲区中,图像就会正确显示在我们的 sRGB LCD 显示器上(其中“正确”意味着它或多或少准确地表示拍摄的真实世界场景)。
当我们开始直接在 sRGB 像素缓冲区上运行任何图像处理算法时,就会出现问题。 请记住,伽玛编码是一种非线性变换,而 sRGB 编码基本上只是一种进行约 γ=1/2.2 伽玛编码的时髦方法。 事实上,你在任何计算机图形文本中发现的所有图像处理算法都会假设具有线性编码光强度的像素数据,这意味着向这些算法提供 sRGB 编码数据将微妙地呈现结果(或者在某些情况下非常明显)错误! 这包括调整大小、模糊、合成、像素值之间的插值、抗锯齿等等,仅举出最常见的操作!
3、不校正伽玛的影响
好了,理论讨论已经够多了,让我看看这些错误实际上是什么样子的! 这正是我们在本节中要做的; 我们将研究直接在 sRGB 数据上运行图像处理算法时最常见的情况,这会导致错误的结果。 除了说明目的之外,这些示例对于发现绘图程序和图像处理库中的伽玛不正确行为或错误也很有用。
必须指出的是,我选择的例子清楚地证明了伽玛不正确的问题。 在大多数情况下,当使用鲜艳、饱和的颜色时,问题最为明显。 使用更柔和的颜色,差异可能不太明显,在某些情况下甚至可以忽略不计。 然而,错误始终存在,图像处理程序应该对所有可能的输入正确工作,而不仅仅是对所有可能图像的 65.23% 来说还可以……此外,在基于物理的渲染领域,伽玛校正是绝对必须的,因为我们会看到的。
3.1 渐变
下图显示了在线性(顶部渐变)和 sRGB 空间(底部渐变)中计算的渐变之间的差异。 请注意 sRGB 值的直接插值如何产生更暗且有时更饱和的图像。

图7:每个渐变对的顶部是gamma校正的,底部无gamma校正
仅从外观来看,人们可能更喜欢 sRGB 空间版本的外观,尤其是最后两个。 然而,这并不是光在现实世界中的表现(想象两个彩色光源照亮白墙;颜色会像线性空间情况一样混合)。
几乎每个人都以错误的方式这样做:CSS 渐变和过渡是错误的(有关详细信息,请参阅此讨论),Photoshop 是错误的(从版本 CS6 开始),甚至没有修复它的选项。
Krita 和 Pixelmator 是两个能够正确实现这一点(以及一般伽玛校正)的绘图程序。 SVG 还允许用户指定是使用线性插值还是 sRGB 空间插值来进行渐变、合成和动画。
3.2 颜色混合
在没有伽玛校正的绘图程序中使用软画笔绘图可能会导致奇怪的深色过渡带和某些鲜艳的颜色组合。 如果你仔细想想,这实际上是渐变问题的一种变体(软画笔的过渡带只不过是一个小渐变)。
一些人在 Adobe 论坛上声称 Photoshop 这样做实际上是在模仿现实生活中混合颜料的工作方式。 嗯,不,这与此无关。 这只是直接处理 sRGB 像素数据的幼稚编程的结果,现在我们仍将其作为默认的遗留行为。

图 8:无伽玛校正的颜色混合的影响。 左边启用gamma校正,右边未启用
3.3 Alpha 混合/合成
作为颜色混合的另一种变化,让我们看看 Alpha 混合如何发挥作用。 我们将首先检查一些彩色矩形。 正如预期的那样,左侧的伽马校正图像模仿了现实生活中光线的表现,而右侧的 sRGB 空间混合则表现出一些奇怪的色调和亮度变化。

图 9:伽马校正对alpha 混合的影响。左图使用gamma校正,右图未使用
将两张照片混合在一起时,假色的出现也很明显。 在左侧的伽马校正图像中,肤色以及红色和黄色被保留,但以自然的方式淡入蓝色图像,而在右侧图像中,整体出现明显的绿色色偏。 同样,这可能是你喜欢的效果,但这并不是 Alpha 合成应该如何准确地工作。

图 10:合成摄影图像时伽玛校正的影响。左图使用gamma校正
3.4 调整图像大小
仅当你的浏览器不对下面的图像进行任何重新缩放时,这些示例才有效。 另请注意,移动设备的屏幕在伽马值方面比常规显示器更不准确,因此为了获得最佳结果,请尝试在台式计算机上查看此结果。
下图包含一个简单的黑白棋盘像素图案(左侧为 100% 缩放,右侧为 400% 缩放)。 黑色像素为 RGB(0,0,0),即显示器能够产生的最小光强度,白色像素为 RGB(255,255,255),即最大强度。 现在,如果你稍微眯着眼睛,你的眼睛就会模糊(平均)来自图像的光线,因此你会看到强度介于绝对黑色和白色之间的灰色(因此被称为 50% 灰色)。

图 11:黑白棋盘像素图案
由此可见,如果我们将图像大小调整 50%,应该会发生类似的平均过程,但现在是根据像素数据进行算法计算。 我们期望得到一个实心矩形,填充与我们眯着眼睛看到的相同的 50% 灰色。
我们来尝试一下吧! 在下图中,A 是棋盘图案,B 是直接在 sRGB 空间中将图案大小调整 50%(使用双三次插值)的结果,C 是在线性空间中调整图案大小,然后转换为 sRGB。
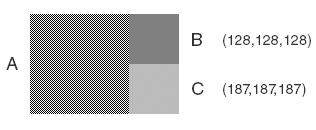
图12:gamma校正对缩放的影像。A)棋盘图 B)无gamma校正 C)使用gamma校正
不出所料,C 给出了正确的结果,但如果没有正确进行伽玛校正,灰色阴影可能与显示器上模糊的棋盘图案不完全匹配。 即使是数学也清楚地表明了这一点:发出的光量是白色像素一半的 50% 灰色像素的 RGB 值应该约为 (186,186,186),伽玛编码计算如下:
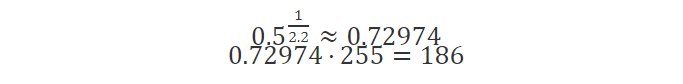
不用担心图像上的 50% 灰度是 RGB(187,187,187。这个微小的差异是因为图像是 sRGB 编码的,但我在这里使用了更简单的伽玛公式进行计算。)
无伽玛校正的调整大小还会导致某些图像出现奇怪的色调变化。 有关更多详细信息,请阅读 Eric Brasseur 关于此问题的出色文章。
3.5 抗锯齿
我想在这一点上,抗锯齿在伽玛校正方面也不例外,这并不奇怪。 γ=2.2 空间中的抗锯齿会导致“平滑像素”过暗(右图);文字显得太重,几乎就像是粗体一样。 在线性空间中运行算法会产生更好的结果(左图),尽管在这种情况下字体看起来有点太细了。 有趣的是,Photoshop 默认情况下使用 γ=1.42 对文本进行抗锯齿处理,这似乎确实产生了最好看的结果(中间图像)。 原因是大多数字体都是针对伽玛不正确的字体光栅器设计的,因此如果你(正确)使用线性空间,那么字体看起来会比应有的更薄:

图13:gamma校正对文本抗锯齿的影响。左)gamma=1.0 中)gamma=1.45 右)gamma=2.2
3.6 基于物理的渲染
如果有一个领域必须保证伽玛正确性,那就是基于物理的渲染 (PBR)。 为了获得逼真的结果,应该在整个图形管道中正确处理伽玛。 有很多方法可以搞砸,但以下是两种最常见的方法:
- 在线性空间中进行计算,但未能将最终图像转换为 sRGB,然后“调整”各种材质和照明参数进行补偿。
- 无法将 sRGB 纹理图像转换为线性空间(或在使用硬件加速时设置 sRGB 标志)。
然后,这两个基本错误通常以各种有趣的方式组合起来,但最终结果总是无法类似于逼真的场景,例如,二次光衰减将不再显得二次,高光将被夸大,并会表现出一些奇怪的色调和饱和度变化 等等。
为了演示使用我自己的光线追踪器的第一个错误,下面的左图显示了一个非常简单但在物理照明精度方面看起来非常自然的图像。 该渲染发生在线性空间中,然后帧缓冲区的内容在写入磁盘之前被转换为 sRGB。
然而,在右侧图像中,最后一个转换步骤被省略,我尝试调整光强度以尝试匹配伽玛校正图像的整体亮度。 嗯,很明显这是行不通的。 一切都显得太反差和过度饱和,所以我们可能需要稍微降低所有材质颜色的饱和度,也许使用更多的补光灯来更接近左图像的外观。 但这是一场失败的战斗; 无论进行多少调整都无法使图像在物理意义上正确,即使我们在具有特定照明设置的特定场景中将其达到可接受的水平,对场景的任何进一步更改都可能需要进行另一轮调整才能使 结果再次看起来很现实。 更重要的是,我们需要选择的材质和照明参数将完全没有任何物理意义; 它们只是一组随机数字,恰好为该特定场景生成看起来不错的图像,因此不能转移到其他场景或照明条件。 这样的工作会浪费很多精力:

图 14:伽玛校正对漫射球体渲染的影响。左图正确使用gamma校正
同样重要的是要指出,3D 渲染中不正确的伽玛处理是某些(大多数是较旧的)游戏中“假塑料 CGI 外观”背后的罪魁祸首之一。 如下图所示,使用没有伽马校正的工作流程几乎不可能渲染逼真的人体皮肤; 亮点永远不会看起来正确。 这催生了一些有问题的做法,例如用反转的色调和各种其他肮脏的东西来补偿镜面贴图中的错误高光,而不是从源头解决问题......
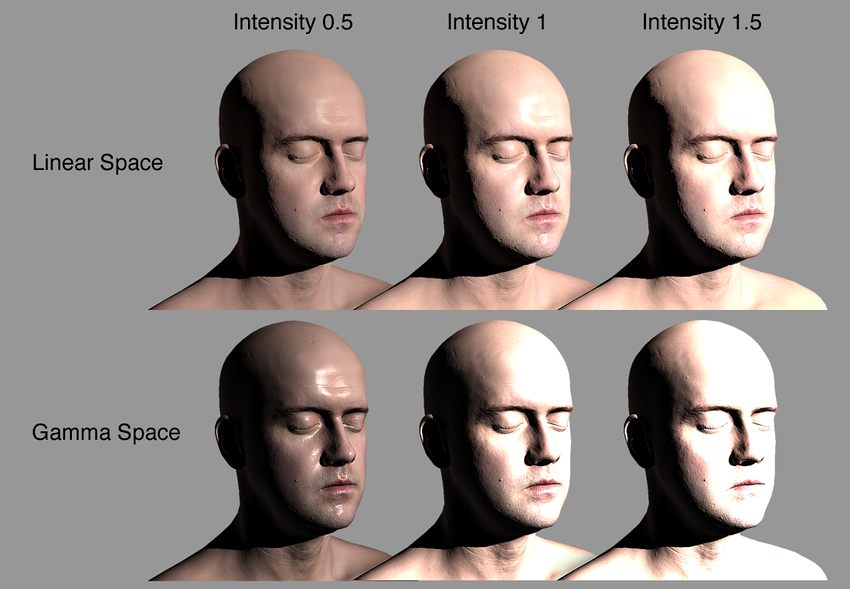
图 15:伽玛校正对头像渲染的影响。
4、结束语
这几乎就是伽玛编码和解码的全部内容。 到目前为止,恭喜你,现在你已成为官方认证的伽马兼容开发人员! :)
回顾一下,对数字图像使用伽马编码的唯一原因是它允许我们在有限的位长度上更有效地存储图像。 它利用了人类视觉的一个特点,即我们以对数方式感知亮度。 大多数图像处理算法都期望像素数据具有线性编码的光强度,因此伽玛编码图像需要首先进行伽玛解码(转换为线性空间),然后才能对其运行这些算法。 通常,结果需要转换回伽玛空间,以将它们存储在磁盘上或在需要伽玛编码值的图形硬件上显示它们(大多数消费级图形硬件属于此类)。 事实上的标准 sRGB 色彩空间使用大约 2.2 的伽玛值。 这是互联网上图像以及大多数显示器、扫描仪和打印机的默认色彩空间。 如有疑问,请使用 sRGB。
从最终用户的角度来看,请记住,大多数应用程序和软件库无法正确处理伽玛,因此在将它们采用到你的工作流程之前,请务必确保进行广泛的测试。 为了实现正确的线性工作流程,链中使用的所有软件都必须 100% 伽玛校正。
如果你是从事图形软件开发的开发人员,请确保你做的是正确的事情。 保持伽玛正确,并始终在软件文档中明确说明你对输入和输出色彩空间的假设。
原文链接:GAMMA权威指南 - BimAnt