Go语言实现深度学习的正向传播和反向传播

文章目录

  • 开发前言
  • 开发理论
  • 图解理论
  • 数据类型
  • 数学函数
  • 数据节点统一抽象
  • 变量数据节点
  • 常量数据节点
  • 单目运算封装
  • 双目运算封装
  • 算子节点统一抽象
  • 基础算子
  • 加法算子
  • 减法算子
  • 乘法算子
  • 除法算子
  • 指数算子
  • 对数算子
  • 正切算子
  • 正弦算子
  • 余弦算子
  • 数据流图
  • 正向传播
  • 反向传播
  • 运行示例
  • 开发总结

开发前言

正向传播是指从神经网络的输入层开始，通过逐层计算和传递，将输入数据一直传递到输出层。在每一层中，通过对输入数据进行加权求和并应用激活函数，得到该层的输出。这个过程可以看作是将输入数据在网络中前进（向前传播），直至得到模型的预测结果。

反向传播是指根据模型的预测结果和实际标签之间的差异，从输出层向输入层反向计算梯度，并利用梯度来更新网络参数。

这篇博客我将使用Go语言实现正向传播和反向传播，帮助你理解其底层的运转规律

项目代码使用纯粹的Go语言标准库实现，不借用任何其它第三方库。用轮子是生活，造轮子是信仰。

我是醉墨居士，我们现在开始吧🤗

开发理论

一个数学函数，由一系列数据和一系列运算方式构成，我们将数据对应为数据节点，将运算方式对应为算子节点，这样我们就可以将数学函数转化为由一系列数据节点和一系列算子节点组成的数据流图

正向传递数据流图，不断运算数据，就是正向传播的过程
反向传递数据流图，不断累加梯度，就是反向传播的过程

图解理论

我画了两张图来表示函数3 * pow(x, 2) + 2 * x + 1的正向传播和反向传播的过程

正向传播图解
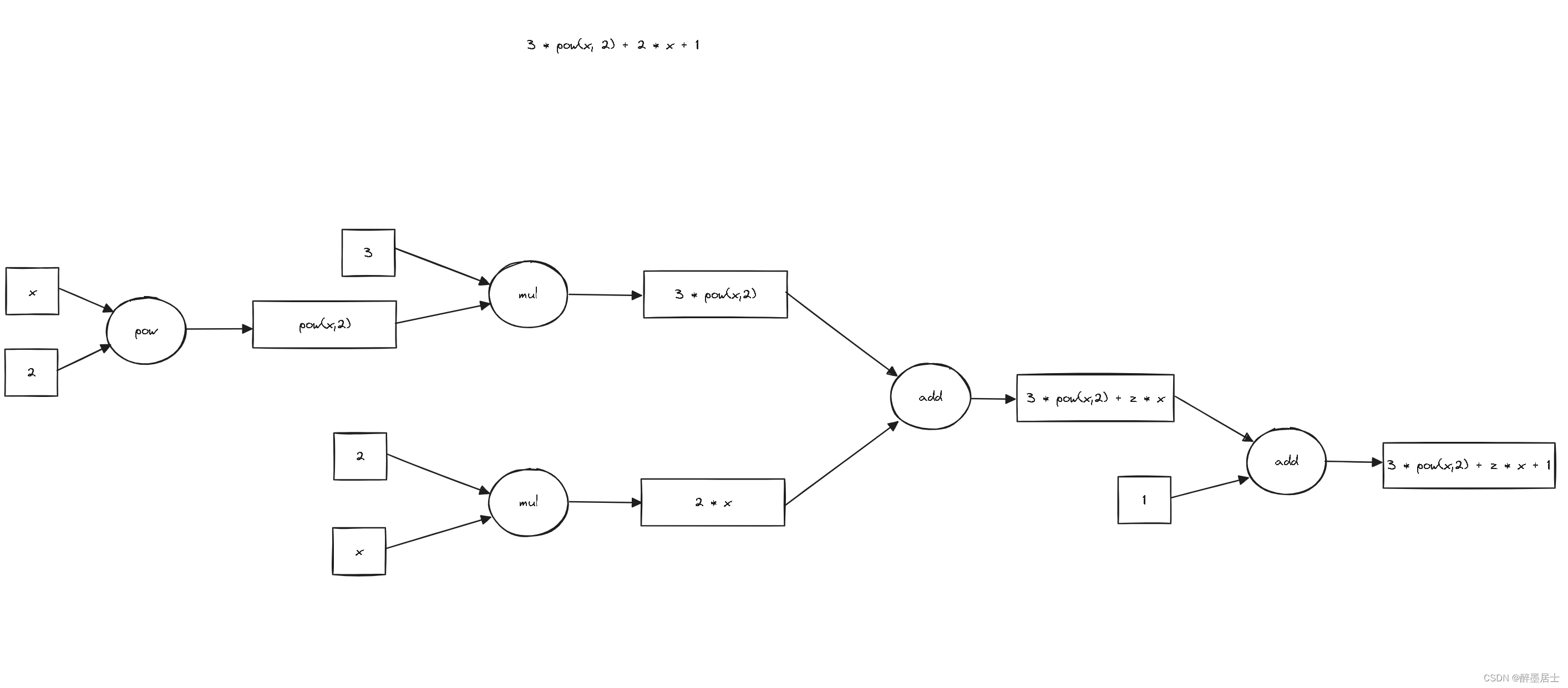
forward

反向传播图解
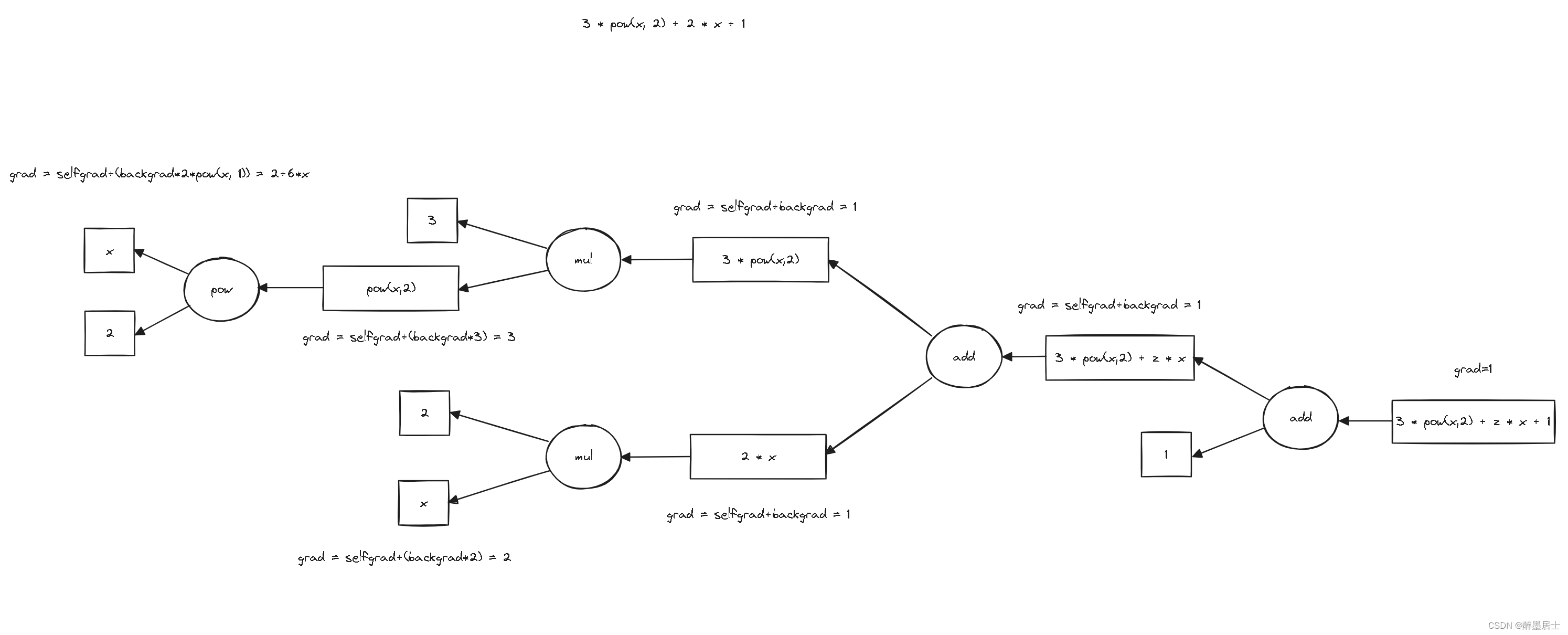
backward

数据类型

data/type

package datatype Type interface {~int | ~int32 | ~int64 |~uint | ~uint32 | ~uint64 |~float32 | ~float64
}

数学函数

math/math.go

package mathimport ("dl/node"stmath "math"
)func Pow[T node.Type](a, b T) T {return T(stmath.Pow(float64(a), float64(b)))
}func Ln[T node.Type](a T) T {return T(stmath.Log(float64(a)))
}func Tan[T node.Type](a T) T {return T(stmath.Tan(float64(a)))
}func Sin[T node.Type](a T) T {return T(stmath.Sin(float64(a)))
}func Cos[T node.Type](a T) T {return T(stmath.Cos(float64(a)))
}

数据节点统一抽象

fm/datanode.go

type DataNode[T data.Type] interface {Data()TSetData(T)Grad()TsetGrad(T)preNode() CalNode[T]backNodes() *[]CalNode[T]fm()FlowMap[T]Add(DataNode[T]) DataNode[T]Sub(DataNode[T]) DataNode[T]Mul(DataNode[T]) DataNode[T]Div(DataNode[T]) DataNode[T]Pow(DataNode[T]) DataNode[T]Ln() DataNode[T]Tan() DataNode[T]Sin() DataNode[T]Cos() DataNode[T]
}

变量数据节点

package fmimport "dl/data"type varDataNode[T data.Type] struct {data Tgrad Tprenode CalNode[T]backnodes []CalNode[T]flowmap FlowMap[T]
}func (n *varDataNode[T]) Data() T {return n.data
}func (n *varDataNode[T]) SetData(i T) {n.data = i
}func (n *varDataNode[T]) Grad() T {return n.grad
}func (n *varDataNode[T]) setGrad(i T) {n.grad = i
}func (n *varDataNode[T]) preNode() CalNode[T] {return n.prenode
}func (n *varDataNode[T]) backNodes() *[]CalNode[T] {return &n.backnodes
}func (n *varDataNode[T]) fm() FlowMap[T] {return n.flowmap
}func (n *varDataNode[T]) Add(node DataNode[T]) DataNode[T] {return calTwo(newAdd[T](), n, node)
}func (n *varDataNode[T]) Sub(node DataNode[T]) DataNode[T] {return calTwo(newSub[T](), n, node)
}func (n *varDataNode[T]) Mul(node DataNode[T]) DataNode[T] {return calTwo(newMul[T](), n, node)
}func (n *varDataNode[T]) Div(node DataNode[T]) DataNode[T] {return calTwo(newDiv[T](), n, node)
}func (n *varDataNode[T]) Pow(node DataNode[T]) DataNode[T] {return calTwo(newPow[T](), n, node)
}func (n *varDataNode[T]) Ln() DataNode[T] {return calOne(newLn[T](), n)
}func (n *varDataNode[T]) Tan() DataNode[T] {return calOne(newTan[T](), n)
}func (n *varDataNode[T]) Sin() DataNode[T] {return calOne(newSin[T](), n)
}func (n *varDataNode[T]) Cos() DataNode[T] {return calOne(newCos[T](), n)
}

常量数据节点

type constDataNode[T data.Type] struct {data      Tprenode   CalNode[T]backnodes []CalNode[T]flowmap   FlowMap[T]
}func (n *constDataNode[T]) Data() T {return n.data
}func (n *constDataNode[T]) SetData(i T) {n.data = i
}
func (n *constDataNode[T]) Grad() T {return 0
}func (n *constDataNode[T]) setGrad(T) {}func (n *constDataNode[T]) preNode() CalNode[T] {return n.prenode
}func (n *constDataNode[T]) backNodes() *[]CalNode[T] {return &n.backnodes
}func (n *constDataNode[T]) fm() FlowMap[T] {return n.flowmap
}func (n *constDataNode[T]) Add(node DataNode[T]) DataNode[T] {return calTwo(newAdd[T](), n, node)
}func (n *constDataNode[T]) Sub(node DataNode[T]) DataNode[T] {return calTwo(newSub[T](), n, node)
}func (n *constDataNode[T]) Mul(node DataNode[T]) DataNode[T] {return calTwo(newMul[T](), n, node)
}func (n *constDataNode[T]) Div(node DataNode[T]) DataNode[T] {return calTwo(newDiv[T](), n, node)
}func (n *constDataNode[T]) Pow(node DataNode[T]) DataNode[T] {return calTwo(newPow[T](), n, node)
}func (n *constDataNode[T]) Ln() DataNode[T] {return calOne(newLn[T](), n)
}func (n *constDataNode[T]) Tan() DataNode[T] {return calOne(newTan[T](), n)
}func (n *constDataNode[T]) Sin() DataNode[T] {return calOne(newSin[T](), n)
}func (n *constDataNode[T]) Cos() DataNode[T] {return calOne(newCos[T](), n)
}

单目运算封装

func calOne[T data.Type](operation CalNode[T], a DataNode[T]) DataNode[T] {*a.fm().calnodes = append(*a.fm().calnodes, operation)*a.backNodes() = append(*a.backNodes(), operation)res := &varDataNode[T]{prenode: operation,flowmap: a.fm(),}*a.fm().datanodes = append(*a.fm().datanodes, res)operation.CalNode().PreNodes = []DataNode[T]{a}operation.CalNode().BackNode = resreturn res
}

双目运算封装

func calTwo[T data.Type] (operation CalNode[T], a, b DataNode[T]) DataNode[T] {if a.fm() != b.fm() {return nil}*a.fm().calnodes = append(*a.fm().calnodes, operation)*a.backNodes() = append(*a.backNodes(), operation)*b.backNodes() = append(*b.backNodes(), operation)res := &varDataNode[T]{prenode: operation,flowmap: a.fm(),}*a.fm().datanodes = append(*a.fm().datanodes, res)operation.CalNode().PreNodes = []DataNode[T]{a, b}operation.CalNode().BackNode = resreturn res
}

算子节点统一抽象

fm/calnode.go

type CalNode[T data.Type] interface {CalNode() *BaseCalNode[T]Forward()Backward()
}

基础算子

type BaseCalNode[T data.Type] struct {PreNodes []DataNode[T]BackNode DataNode[T]
}

加法算子

type AddNode[T data.Type] BaseCalNode[T]func newAdd[T data.Type]() CalNode[T] {basenode := &BaseCalNode[T]{}return (*AddNode[T])(basenode)
}func (n *AddNode[T]) CalNode() *BaseCalNode[T] {return (*BaseCalNode[T])(n)
}func (n *AddNode[T]) Forward() {n.BackNode.SetData(n.CalNode().PreNodes[0].Data() + n.CalNode().PreNodes[1].Data())
}func (n *AddNode[T]) Backward() {// selfgrad + backgradgrad0 := n.PreNodes[0].Grad() + n.BackNode.Grad()// selfgrad + backgradgrad1 := n.PreNodes[1].Grad() + n.BackNode.Grad()n.PreNodes[0].setGrad(grad0)n.PreNodes[1].setGrad(grad1)
}

减法算子

type SubNode[T data.Type] BaseCalNode[T]func newSub[T data.Type]() CalNode[T] {basenode := &BaseCalNode[T]{}return (*SubNode[T])(basenode)
}func (n *SubNode[T]) CalNode() *BaseCalNode[T] {return (*BaseCalNode[T])(n)
}func (n *SubNode[T]) Forward() {n.BackNode.SetData(n.CalNode().PreNodes[0].Data() - n.CalNode().PreNodes[1].Data())
}func (n *SubNode[T]) Backward() {// selfgrad + backgradgrad0 := n.PreNodes[0].Grad() + n.BackNode.Grad()// selfgrad - backgradgrad1 := n.PreNodes[1].Grad() - n.BackNode.Grad()n.PreNodes[0].setGrad(grad0)n.PreNodes[1].setGrad(grad1)
}

乘法算子

type MulNode[T data.Type] BaseCalNode[T]func newMul[T data.Type]() CalNode[T] {basenode := &BaseCalNode[T]{}return (*MulNode[T])(basenode)
}func (n *MulNode[T]) CalNode() *BaseCalNode[T] {return (*BaseCalNode[T])(n)
}func (n *MulNode[T]) Forward() {n.BackNode.SetData(n.CalNode().PreNodes[0].Data() * n.CalNode().PreNodes[1].Data())
}func (n *MulNode[T]) Backward() {a := n.PreNodes[0].Data()b := n.PreNodes[1].Data()backgrad := n.BackNode.Grad()// selfgrad + (backgrad * b)grad0 := n.PreNodes[0].Grad() + (backgrad * b)// selfgrad + (backgrad * a)grad1 := n.PreNodes[1].Grad() + (backgrad * a)n.PreNodes[0].setGrad(grad0)n.PreNodes[1].setGrad(grad1)
}

除法算子

type DivNode[T data.Type] BaseCalNode[T]func newDiv[T data.Type]() CalNode[T] {basenode := &BaseCalNode[T]{}return (*DivNode[T])(basenode)
}func (n *DivNode[T]) CalNode() *BaseCalNode[T] {return (*BaseCalNode[T])(n)
}func (n *DivNode[T]) Forward() {n.BackNode.SetData(n.CalNode().PreNodes[0].Data() / n.CalNode().PreNodes[1].Data())
}func (n *DivNode[T]) Backward() {a := n.PreNodes[0].Data()b := n.PreNodes[1].Data()backgrad := n.BackNode.Grad()// selfgrad + (backgrad / b)grad0 := n.PreNodes[0].Grad() + (backgrad / b)// selfgrad - (backgrad * a / pow(b, 2))grad1 := n.PreNodes[1].Grad() - (backgrad * a / math.Pow(b, 2))n.PreNodes[0].setGrad(grad0)n.PreNodes[1].setGrad(grad1)
}

指数算子

type PowNode[T data.Type] BaseCalNode[T]func newPow[T data.Type]() CalNode[T] {basenode := &BaseCalNode[T]{}return (*PowNode[T])(basenode)
}func (n *PowNode[T]) CalNode() *BaseCalNode[T] {return (*BaseCalNode[T])(n)
}func (n *PowNode[T]) Forward() {n.BackNode.SetData(math.Pow(n.CalNode().PreNodes[0].Data(), n.CalNode().PreNodes[1].Data()))
}func (n *PowNode[T]) Backward() {a := n.PreNodes[0].Data()b := n.PreNodes[1].Data()backgrad := n.BackNode.Grad()// selfgrad + (backgrad * b * pow(a, b-1))grad0 := n.PreNodes[0].Grad() + (backgrad * b * math.Pow(a, b-1))// selfgrad + (backgrad * pow(a, b) * ln(a))grad1 := n.PreNodes[1].Grad() + (backgrad * math.Pow(a, b) * math.Ln(a))n.PreNodes[0].setGrad(grad0)n.PreNodes[1].setGrad(grad1)
}

对数算子

type LnNode[T data.Type] BaseCalNode[T]func newLn[T data.Type]() CalNode[T] {basenode := &BaseCalNode[T]{}return (*LnNode[T])(basenode)
}func (n *LnNode[T]) CalNode() *BaseCalNode[T] {return (*BaseCalNode[T])(n)
}func (n *LnNode[T]) Forward() {n.BackNode.SetData(math.Ln(n.CalNode().PreNodes[0].Data()))
}func (n *LnNode[T]) Backward() {a := n.PreNodes[0].Data()backgrad := n.BackNode.Grad()// selfgrad + (backgrad / a)grad0 := n.PreNodes[0].Grad() + (backgrad / a)n.PreNodes[0].setGrad(grad0)
}

正切算子

type TanNode[T data.Type] BaseCalNode[T]func newTan[T data.Type]() CalNode[T] {basenode := &BaseCalNode[T]{}return (*TanNode[T])(basenode)
}func (n *TanNode[T]) CalNode() *BaseCalNode[T] {return (*BaseCalNode[T])(n)
}func (n *TanNode[T]) Forward() {n.BackNode.SetData(math.Tan(n.CalNode().PreNodes[0].Data()))
}func (n *TanNode[T]) Backward() {a := n.PreNodes[0].Data()backgrad := n.BackNode.Grad()// selfgrad + (backgrad / pow(cos(a), 2))grad0 := n.PreNodes[0].Grad() + (backgrad / math.Pow(math.Cos(a), 2))n.PreNodes[0].setGrad(grad0)
}

正弦算子

type SinNode[T data.Type] BaseCalNode[T]func newSin[T data.Type]() CalNode[T] {basenode := &BaseCalNode[T]{}return (*SinNode[T])(basenode)
}func (n *SinNode[T]) CalNode() *BaseCalNode[T] {return (*BaseCalNode[T])(n)
}func (n *SinNode[T]) Forward() {n.BackNode.SetData(math.Sin(n.CalNode().PreNodes[0].Data()))
}func (n *SinNode[T]) Backward() {a := n.PreNodes[0].Data()backgrad := n.BackNode.Grad()// selfgrad + (backgrad * cos(a))grad0 := n.PreNodes[0].Grad() + (backgrad * math.Cos(a))n.PreNodes[0].setGrad(grad0)
}

余弦算子

type CosNode[T data.Type] BaseCalNode[T]func newCos[T data.Type]() CalNode[T] {basenode := &BaseCalNode[T]{}return (*CosNode[T])(basenode)
}func (n *CosNode[T]) CalNode() *BaseCalNode[T] {return (*BaseCalNode[T])(n)
}func (n *CosNode[T]) Forward() {n.BackNode.SetData(math.Cos(n.CalNode().PreNodes[0].Data()))
}func (n *CosNode[T]) Backward() {a := n.PreNodes[0].Data()backgrad := n.BackNode.Grad()// selfgrad - (backgrad * sin(a))grad0 := n.PreNodes[0].Grad() - (backgrad * math.Sin(a))n.PreNodes[0].setGrad(grad0)
}

数据流图

type FlowMap[T data.Type] struct {calnodes  *[]CalNode[T]datanodes *[]DataNode[T]
}func NewFlowMap[T data.Type]() *FlowMap[T] {calnodes := make([]CalNode[T], 0)datanods := make([]DataNode[T], 0)return &FlowMap[T]{calnodes:  &calnodes,datanodes: &datanods,}
}func (m FlowMap[T]) NewData() DataNode[T] {node := &varDataNode[T]{backnodes: make([]CalNode[T], 0),flowmap:   m,}*m.datanodes = append(*m.datanodes, node)return node
}func (m FlowMap[T]) NewConstData(i T) DataNode[T] {return &constDataNode[T]{backnodes: make([]CalNode[T], 0),data:      i,flowmap:   m,}
}

正向传播

func (m FlowMap[T]) Forward() {n := len(*m.calnodes)for i := 0; i < n; i++ {(*m.calnodes)[i].Forward()}
}

反向传播

func (m FlowMap[T]) Backward() {for i := len(*m.datanodes) - 1; i >= 0; i-- {(*m.datanodes)[i].setGrad(0)}n := len(*m.calnodes)-1(*m.calnodes)[n].CalNode().BackNode.setGrad(1)for i := n; i >= 0; i-- {(*m.calnodes)[i].Backward()}
}

运行示例

我们的运行示例使用理论图解的那个例子： 3 * pow(x, 2) + 2 * x + 1

// 3 * pow(x, 2) + 2 * x + 1
func main() {m := fm.NewFlowMap[float64]()x := m.NewData()three := m.NewConstData(3)two := m.NewConstData(2)one := m.NewConstData(1)res := three.Mul(x.Pow(two)).Add(two.Mul(x)).Add(one)x.SetData(2)m.Forward()m.Backward()// data = 3 * pow(2, 2) + 2 * 2 + 1 = 17// grad = 2 + 6 * x = 14fmt.Println("x=2 -> ", "res.data =", res.Data(), ",", "x.grad =", x.Grad())x.SetData(3)m.Forward()m.Backward()// data = 3 * pow(3, 2) + 2 * 3 + 1 = 34// grad = 2 + 6 * x = 20fmt.Println("x=3 -> ", "res.data =", res.Data(), ",", "x.grad =", x.Grad())x.SetData(4)m.Forward()m.Backward()// data = 3 * pow(4, 2) + 2 * 4 + 1 = 57// grad = 2 + 6 * x = 26fmt.Println("x=4 -> ", "res.data =", res.Data(), ",", "x.grad =", x.Grad())
}

运行结果
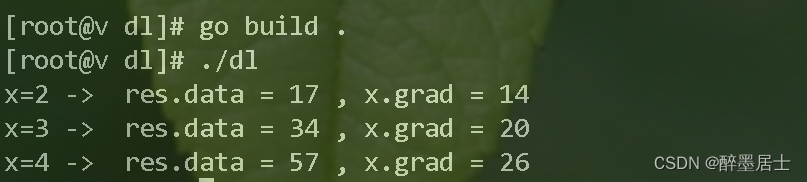
result

开发总结

恭喜你，我们一起使用Go语言完成了深度学习的正向传播和反向传播，希望这个项目能让你有所收获😊

我的特色就是用最简单的方式帮助你学会最硬核的知识，一起加油吧❤️

我是醉墨居士，之前这个账号改了好几次名称，从此之后这个账号的名称大概率不会再变动😜

如果有什么错误，请你评论区或者私信我指出，让我们一起进步✌️

请你多多关注我，开发这个项目，并且整理总结，花费了很多的精力，博客热度越高，更新速度越快😎

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/239421.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

mac安装elasticsearch

mac安装elasticsearch

下载地址&#xff1a; Past Releases of Elastic Stack Software | Elastic https://www.elastic.co/cn/downloads/past-releases#elasticsearch 选择7.10版本 进入es bin目录下执行启动命令 ./elasticsearch 会报错 ./elasticsearch-env: line 126: syntax error near u…
阅读更多...
YOLOv8如何输出COCO指标

YOLOv8如何输出COCO指标

1、先正常python train 一个模型 yolo taskdetect modetrain model/home//v8/v8-ori-x/yolov8x.pt data/home/v8/v8-ori-x/ultralytics/cfg/datasets/111.yaml epochs300 batch16 device62、再正常python val --各种参数 --save_jsonTrue&#xff0c;这一步的作用是要生成自己…
阅读更多...
linux上编写进度条

linux上编写进度条

目录 一、预备的两个小知识1、缓冲区2、回车与换行 二、倒计时程序三、编写入门的进度条四、编写一个正式的五、模拟实现和下载速度相关的进度条 一、预备的两个小知识 1、缓冲区 首先认识一下缓冲区&#xff1a;先写一个.c文件如下&#xff1a; 我们执行一下这个程序时&…
阅读更多...
主成分分析例题 （多元统计分析期末复习）

主成分分析例题 （多元统计分析期末复习）

例一 给定X的协差阵&#xff0c;对其进行主成分分析, &#xff08;1&#xff09;求出每个主成分的贡献率&#xff1b; &#xff08;2&#xff09;求出每个原始变量的信息提取率&#xff1b; 解&#xff1a;对于主成分分析的题&#xff0c;一般来说&#xff0c;题目给定一个协方…
阅读更多...
Verilog inout 端口使用和仿真

Verilog inout 端口使用和仿真

inout端口是Verilog中一种特殊的端口类型&#xff0c;它可以实现双向的数据传输&#xff0c;既可以作为输入&#xff0c;也可以作为输出。inout端口通常用于实现管脚复用、三态缓冲器、总线驱动等功能。inout端口的使用需要注意以下几个方面&#xff1a; inout端口必须声明为wi…
阅读更多...
海云安谢朝海：开发安全领域大模型新实践 人工智能助力高效安全左移

海云安谢朝海：开发安全领域大模型新实践 人工智能助力高效安全左移

2023年11月29日&#xff0c;2023中国&#xff08;深圳&#xff09;金融科技大会成功举行&#xff0c;该会议是深圳连续举办的第七届金融科技主题年度会议&#xff0c;也是2023深圳国际金融科技节重要活动之一。做好金融工作&#xff0c;需要兼顾创新与安全&#xff0c;当智能体…
阅读更多...
系列十七、理解SpringBoot中的starter 自定义一个starter

系列十七、理解SpringBoot中的starter 自定义一个starter

一、概述 作为后端Java程序员&#xff0c;基本上公司的日常开发都是基于SpringBoot进行的&#xff0c;我们使用SpringBoot也是沉醉于它的各种各样的starter带给我们的便利&#xff0c;这些starter为我们带来了众多的自动化配置&#xff0c;通过这些自动化配置&#xff0c;我们可…
阅读更多...
mysql中除了InnoDB以外的其它存储引擎

mysql中除了InnoDB以外的其它存储引擎

参考资料&#xff1a;https://dev.mysql.com/doc/refman/8.0/en/storage-engines.html MyISAM存储引擎 https://dev.mysql.com/doc/refman/8.0/en/myisam-storage-engine.html MyISAM 存储引擎是基于比较老的ISAM存储引擎&#xff08;ISAM已经不再可用&#xff09;&#xff…
阅读更多...
[论文精读]利用大语言模型对扩散模型进行自我修正

[论文精读]利用大语言模型对扩散模型进行自我修正

本博客是一篇最新论文的精读&#xff0c;论文为UC伯克利大学相关研究者新近(2023.11.27)在arxiv上上传的《Self-correcting LLM-controlled Diffusion Models》 。 内容提要: 现有的基于扩散的文本到图像生成模型在生成与复杂提示精确对齐的图像时仍然存在困难,尤其是需要数值和…
阅读更多...
前缀和 LeetCode1094 拼车

前缀和 LeetCode1094 拼车

1094. 拼车 车上最初有 capacity 个空座位。车 只能 向一个方向行驶&#xff08;也就是说&#xff0c;不允许掉头或改变方向&#xff09; 给定整数 capacity 和一个数组 trips , trip[i] [numPassengersi, fromi, toi] 表示第 i 次旅行有 numPassengersi 乘客&#xff0c;接…
阅读更多...
SATA模块物理层OOB信号分析总结（三）

SATA模块物理层OOB信号分析总结（三）

目录 一、简介二、总体解析2.1 OOB作用2.2 OOB信号的组成2.3 总体phy link过程2.4 整体PHY LINK Trace2.5 PHY LINK状态查询 三、其他相关链接1、SATA模块之HBA卡开发总结&#xff08;一&#xff09;2、SATA信息传输FIS结构总结&#xff08;二&#xff09;3、PCIe物理层总结-PC…
阅读更多...
什么是CAS, 什么是AQS

什么是CAS, 什么是AQS

文章目录 什么是CAS, 什么是AQSCASAQS 什么是CAS, 什么是AQS CAS AQS AQS 全称是AbstractQueuedSynchronizer&#xff0c; 是juc 下一个核心的抽象类&#xff0c;用于构建各种同步器和锁 比如我们熟悉的 ReentrantLock、ReadWriteLock、CountDownLatch等等是基于AQS. 首先在…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023