高级搜索——ST表，离线RMQ问题-编程知识

高级搜索——ST表，离线RMQ问题

文章目录

- 前言
- 可重复贡献问题
- ST表的定义
- ST表的存储结构
- ST表的预处理
- - 预处理的实现
- ST表的区间查询
- - 对于k的获取
  - 区间查询的实现
- OJ链接

前言

对于查询区间最值的方法，我们常用的就是线段树，树状数组，单调队列，而树状数组更适合用于快速求区间和，而单调队列维护区间最值只在特殊情况下适用，最无解的线段树空间开销大，而且有一定的代码量，它在动态维护区间最值上基本上可以说是最优解，但是如果是离线询问的话，本文将介绍的ST表，代码量远小于线段树，而且还能达到不错的时间复杂度。

可重复贡献问题

可重复贡献问题是指，对于运算opt ，任意操作数x，都满足x opt x = x。例如，max(x , x) = x , gcd(x , x) = x，因此，RMQ(区间最值查询)和区间gcd问题也是可重复贡献问题。

ST表的定义

ST表（Sparse Table）稀疏表，是一种适用于符合结合律且可重复贡献的信息查询的数据结构，如区间最大值、最小值、最大公因数，最小公倍数，按位或，按位与等。在处理RMQ（查询区间最值）问题时，通过倍增思想，我们可以以O(nlogn)预处理，从而实现O(1)查询。

ST表的存储结构

ST表的存储结构非常简单，就是一个二维数组f , 其中，f[i][j]代表以第i个数为起点，长度为2^j次方的区间内的最值。

我们接下来均以最大值做讨论。

#define N 100010
int f[N][20];

ST表的预处理

我们如何去获取这样一个ST表呢？

对于一个大问题我们可以将其拆解为若干个小问题，利用其可重复贡献性来逐步得到我们问题的答案。

ST表以倍增法做递推来预处理ST表，其实是一种自下而上的动态规划。

对于一个区间最大值而言，显然等于两个等长子区间最大值的最大值。那么根据我们f[i][j]的定义，可有如下递推公式：
$f[i][j] = max(f[i][j-1] , f[1+(i+2^{j-1}][j-1])$
那么我们只需要固定区间长度然后枚举起点，自下而上进行动态规划即可，由于区间长度每次倍增，所以不难得出我们的时间复杂度为O(nlogn)

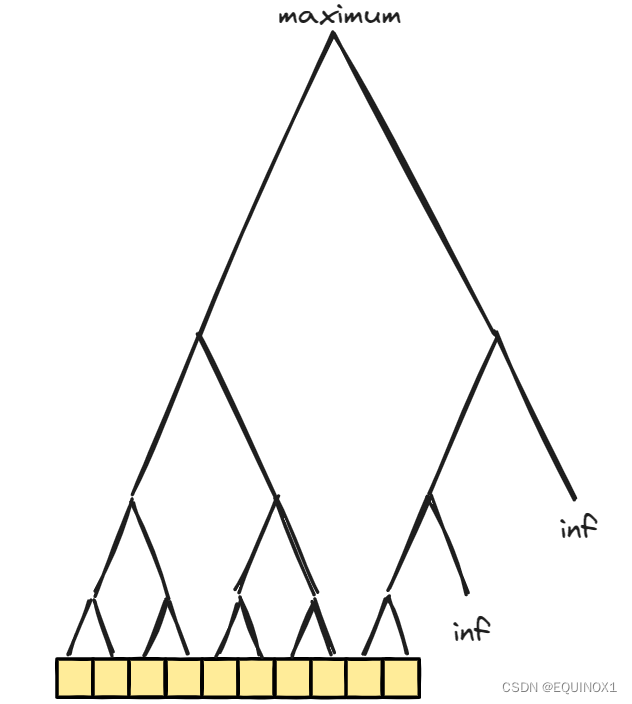
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

预处理的实现

实现流程：

目标序列arr，长度为n，下标从1开始
初始化f[i][0]为arr[i]
枚举长度j，然后枚举起点i进行状态转移
注意区间边界和位运算优先级

    for (int i = 1; i <= n; i++)f[i][0] = arr[i];for (int j = 1; j <= 20; j++)for (int i = 1; i + (1 << j) - 1 <= n; i++)f[i][j] = min(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);

ST表的区间查询

我们ST表能够实现对于任意区间[l , r](1<= l,r <=n)内的最值查询，那么是如何实现的呢？

我们已经知道了区间最值可以有子区间最值转移而来，那么对于区间[l , r]我们一定可以找到k，使得
$2^{k}\le\log_{2}{(r - l + 1)}<2^{k+1}$
那么我们可以得到分别以l为左端点和以r为右端点的两个长度为2^k的区间，这两个区间的最值的最值就是我们[l , r]区间内的最值。
$query(l , r) = max(f[l][k],f[r-2^{k}+1][k])$
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

对于k的获取

k显然就是log2 (r - l + 1)向下取整，这里我们有两种方案获取log2值

F1 递推预处理

观察下2^n求和公式很容易想明白这个递推，我们O(n)预处理，分摊每次取log2为O(1)

//int Log2[N]{0};
for (int i = 2; i <= n; ++i)Log2[i] = Log2[i / 2] + 1;

F2 直接用cmath里的log2

区间查询的实现

    for (int i = 0; i < n; i++){//l = read(), r = read();cin >> l >> r;int k = log2(r - l + 1);cout << min(f[l][k], f[r - (1 << k) + 1][k]) << " ";//write(min(f[l][k], f[r - (1 << k) + 1][k])), putchar(' ');}

到此ST表的原理及实现就结束了，代码量非常少，在处理离线查询跟线段树的代码量比起来，显然这个出错率更低。

我们上面都是以最大值为例进行实现的，在实际应用中只要是满足结合律且可重复贡献的信息查询都在ST表的解决范围内，因为ST表能够对两个交集非空的子区间进行信息合并，这也就是重复贡献的精妙之处。