C语言WFC实现绘制Lagrange插值多项式曲线的函数-编程知识

C语言WFC实现绘制Lagrange插值多项式曲线的函数

前言（引用）：

拉格朗日多项式插值
插值方法有许多，常用的、基本的有：拉格朗日多项式插值、牛顿插值、分段线插值、Hermite插值和三次样条插值。这里只将一下拉格朗日多项式插值法：

方法应用
通缩点说，已知n+1个点x1，x2，…，xn的函数值，可以使用lagrange插值求出一个n次多项式插值函数f(x),f(x)是接近未知原函数p(x)的函数，根据插值函数f(x)求出p(x)的未知点

具体引入
已知一个未知函数f（x）的三个点（x1,y1）、（x2,y2）、（x3,y3）

存在使用一个多项式函数经过这三个点，呈现为一根曲线

因此进行合理假设，此曲线为一个二次多项式

拉格朗日认为可通过三根两次曲线来得到这根二次曲线。

关键

因此假设了三根曲线

第一根曲线f1（x），在x1点处，取值为1，其余两点（x2,y2）、（x3,y3）取值为0

第二根曲线f2（x），在x2点处，取值为1，其余两点（x1,y1）、（x3,y3）取值为0

第三根曲线f3（x），在x3点处，取值为1，其余两点（x1,y1）、（x2,y2）取值为0

所以可得到

y1f1（x）曲线可以保证，在x1处，取值为y1，其余两点取值为0

y2f2（x）曲线可以保证，在x2处，取值为y2，其余两点取值为0

y3f3（x）曲线可以保证，在x3处，取值为y3，其余两点取值为0

可以说这三根曲线就可以组成需要得到的那根二次曲线

那么，f（x）=y1f1（x）+y2f2（x）+y3f3（x）
原文链接：https://blog.csdn.net/weixin_47210960/article/details/119428254

代码实现：

//拉格朗日插值法
void CCGDrawingView::Lagrange(double* x,double* y, int num, CDC* pDC)
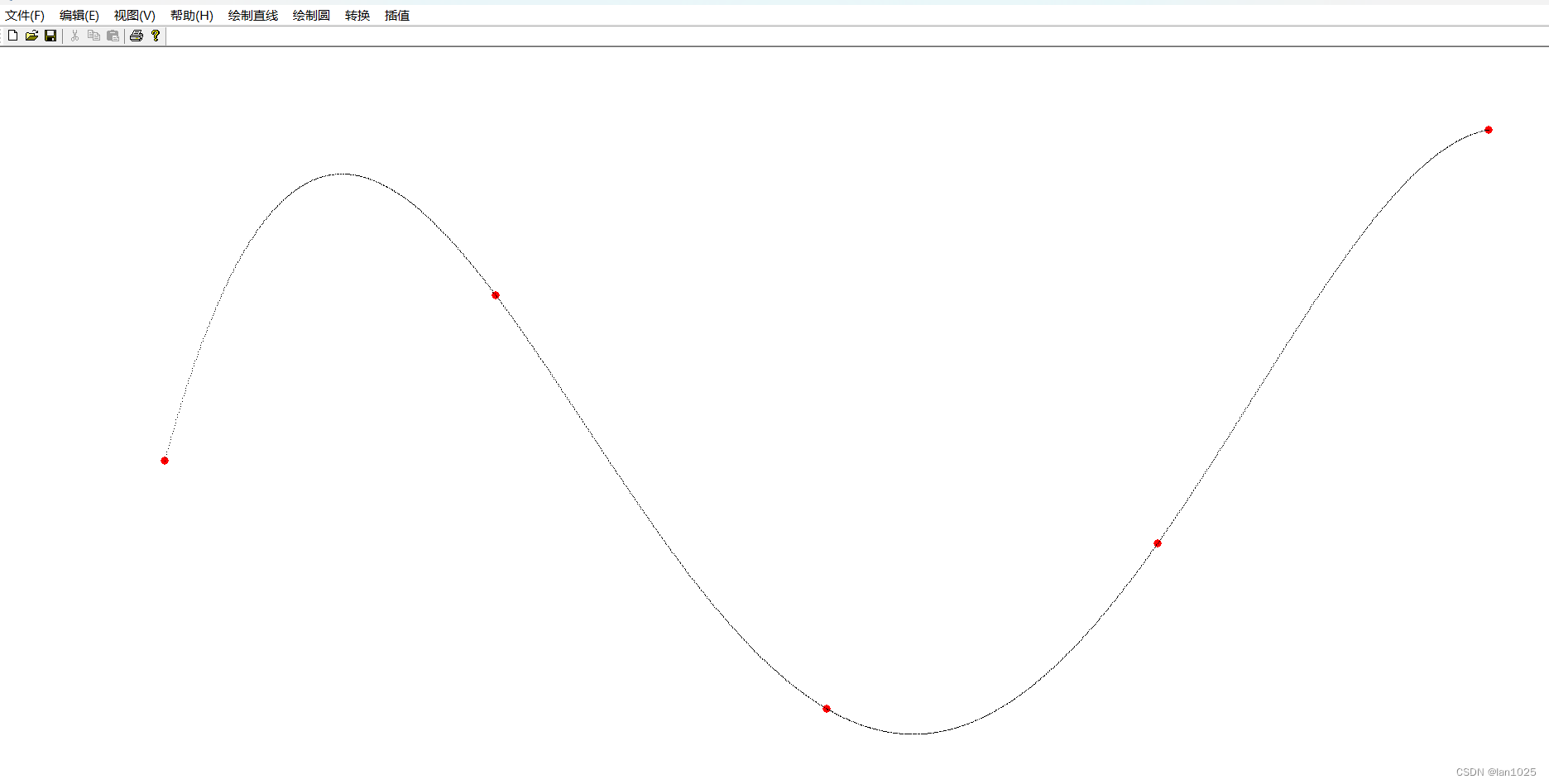
{//画原始点CPen redPen(PS_SOLID, 1, RGB(255, 0, 0));CBrush redBrush(RGB(255, 0, 0));CPen* pOldPen = pDC->SelectObject(&redPen);CBrush* pOldBrush = pDC->SelectObject(&redBrush);for (int i = 0; i < num; ++i) {pDC->Ellipse(int(x[i] - 5),int(y[i] - 5),int(x[i] + 5),int(y[i] + 5));}//绘制Lagrange插值多项式曲线pDC->SelectObject(pOldPen);pDC->SelectObject(pOldBrush);for (int i = (int)x[0]; i <= (int)x[num - 1]; ++i) {double t = i;double tx = 0.0;double ty = 0.0;for (int j = 0; j < num; ++j) {double g = 1.0;//计算基函数的值for (int m = 0; m < num; ++m) {if (m == j)continue;g = g * (t - x[m]) / (x[j] - x[m]);}//根据基函数的值计算坐标tx += x[j] * g;ty += y[j] * g;}//画像素点pDC->SetPixel((int)tx, (int)ty, RGB(0, 0, 0));}
}