VisualStudio反汇编功能使用
使用方法
到达断点时:Ctrl+K(松开)+G(后按)唤出反汇编界面,就可以看到当前代码对应的汇编语言了
注意:进入反汇编窗口后可以F10单次调试一条汇编指令
其他:
- 打开调试-窗口-寄存器 可以查看寄存器数值
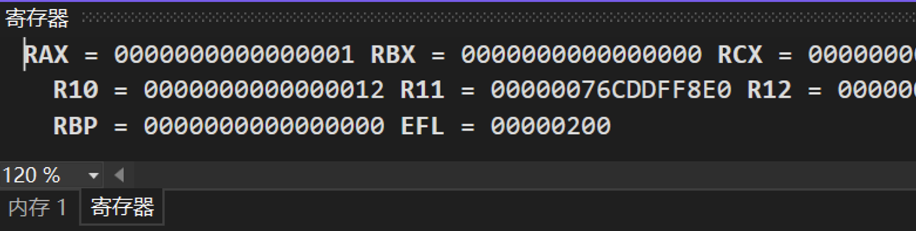
- 打开调试-窗口-内存 可以查看内存数值,支持搜索,将反汇编中的地址拷贝进搜索框可以定位你想要查看的内存地址的值
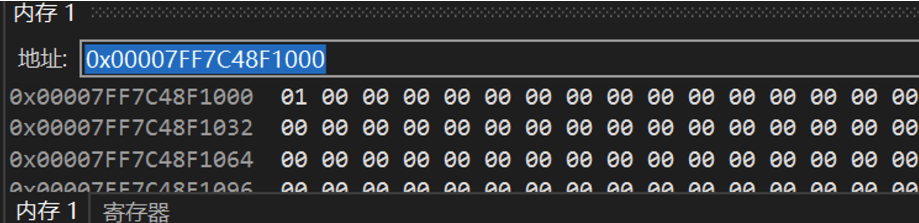
搭配食用为佳
常用寄存器
详见*X86-64寄存器介绍

windows X86寄存器命名规则
r前缀:64位寄存器
e前缀:32位寄存器
后缀L:集群从的低八位
后缀H:寄存器的9~16位
既然这样,那就只讨论中间的名字,不考虑前后缀,看有哪些寄存器
寄存器分类(大小为16位)
通用寄存器
ax:accumulator register 累加寄存器
bx:base register 基址寄存器 存访问地址
cx:count register 计数寄存器
dx:data register 数据寄存器
索引寄存器
bp:base pointer 基址指针 用来定位栈底
sp:stack pointer 栈指针,栈寄存器的偏移量,用来定位栈顶
si:source index 变址寄存器 拷贝源字符串
di:destination index 目标变址寄存器 复制目标字符串
控制寄存器
ip:instruction pointer 只读的指令寄存器指针 不可拆分 记录下一条指令位置
flag:储存当前状态,详见寄存器详解
普通寄存器
r8~r15 可根据无\D\W\B后缀来分割为更小的寄存器,最大64位(8B)
ymm0~ymm15 存储双精度和单精度浮点数,最大256位(32B),能放4个双精度,8个单精度,一个ymm寄存器可以拆分成两个xmm
寄存器分类(大小为8位)
遵循前面提到的前后缀规则,16位寄存器可以分为两个8位寄存器:
ah、al
bh,bl
ch,cl
dh,dl
寄存器分类(大小为32位)
eax,ebx,ecx,edx
寄存器分类(大小为64位)
rax, rbx, rcx, rdx
常用指令
mov:move data 移动数据 movz,movs是0扩展和符号扩展指令,将较小的数从寄存器或内存转移到寄存器中
lea destination, source:load effective address 加载有效地址 是mov指令的变形
详见:
X86汇编指南
其他资料
寻址方式
反汇编分析
反汇编分析类和对象
指令翻译(仅供参考)
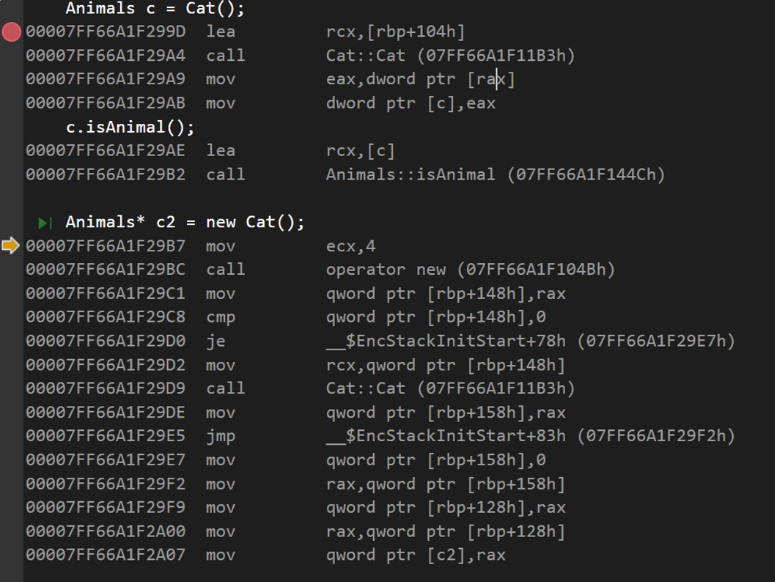
尝试把下面的指令翻译出来
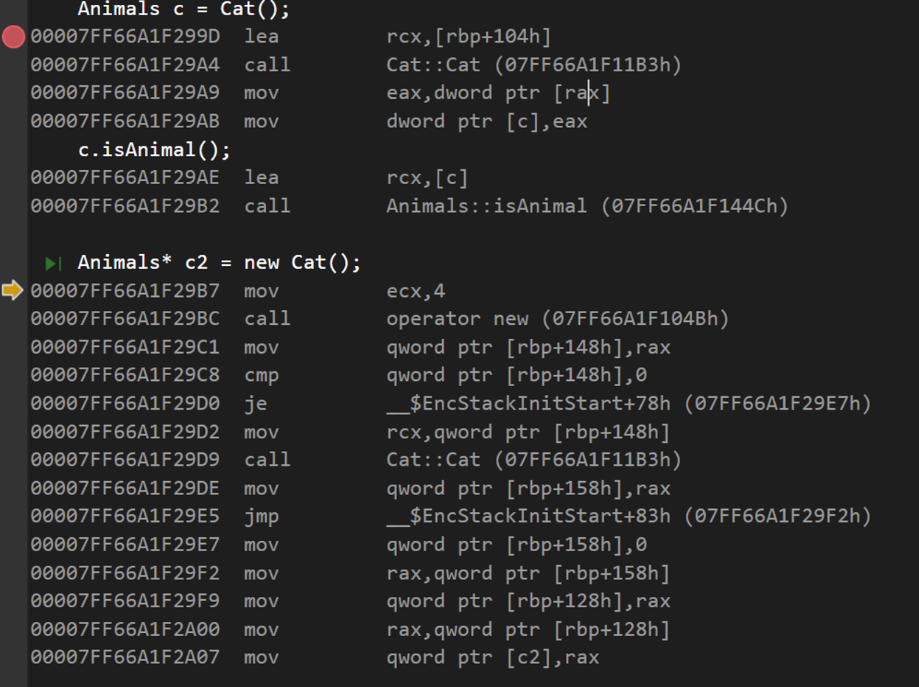
lea rcx, [rbp+104h] 将内存中[rbp+104h](栈底地址+104h,h说明是16进制)的数据放入rcx寄存器
call 通过构造函数Cat的函数指针07FF66A1F11B3h进行调用
mov eax,dword ptr [rax] 将rax寄存器的一个double word指针指向的内容移动到eax
mov dword ptr [c], eax 将eax的值移到内存单元c中一个double word指针的位置lea rcx,[c] 将内存单元c的数据取出并放入rcx中
call 通过isAnimal的函数指针调用该函数mov ecx 4 将立即数4移入ecx寄存器
call 调用new运算符
mov qword ptr [rbp+148h],rax 将rax的值移入[rbp+148h]的内存位置
cmp qword ptr [rbp+148h],0 检查[rbp+148h]的内存位置数是否为0
je 相等则跳转到该地址:stack初始化地址+78h
mov rcx,qword ptr [rbp+148h] 把内存[rbp+148h]的数据移动到rcx中
call 通过构造函数Cat的函数指针07FF66A1F11B3h进行调用
mov qword ptr [rbp+158h],rax 将rax的值移入[rbp+158h]的内存位置
jmp 无条件跳转到stack初始化地址+83h