一、递归的两个特点

1、要自己调用自己

2、递归函数里要有结束条件。

二、汉诺塔问题

        有三根柱子，现在在一根柱子上，从下往上，按照大小顺序摞着很多盘子。现在要把这些盘子全部放到另一根柱子上，且盘子依然按照从大到小顺序摞着。

要求：每次只能移动一个盘子，在小盘子上不能放大盘子。

原理：

当盘子个数为n个时：

第一步：把n-1个盘子，从A经过C移动到B；

第二步：把第n个盘子，从A移动到C；

第三步：把n-1个盘子从B经过A移动到C。

代码实现：

# 把两个盘子从A柱子移动到C柱子
def hanoi(n, a, b, c):if n > 0:hanoi(n - 1, a, c, b)print("把%s移动到%s" % (a, c))hanoi(n - 1, b, a, c)hanoi(2, "A", "B", "C")# 结果：
把A移动到B
把A移动到C
把B移动到C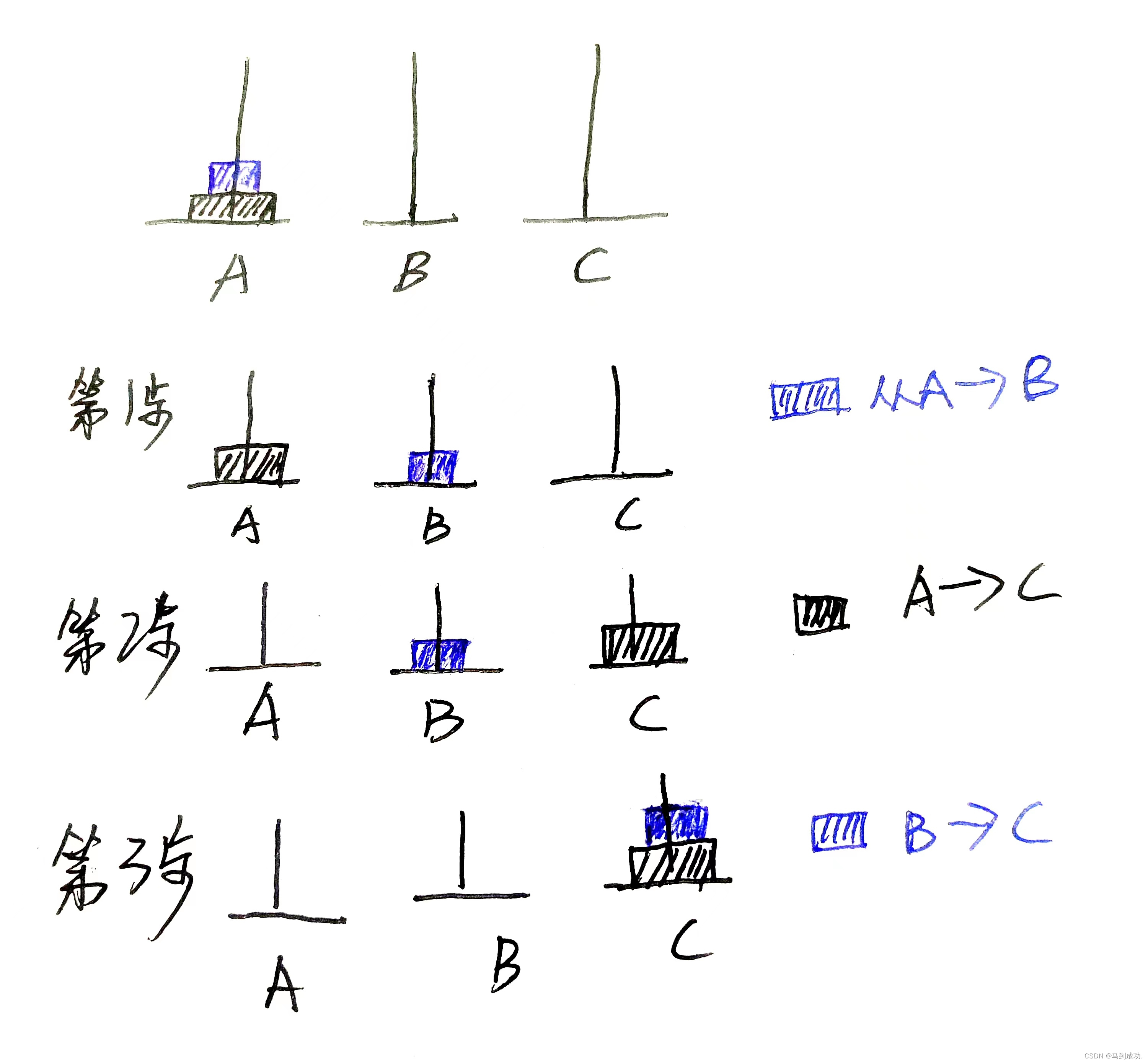

# 移动三个盘子
def hanoi(n, a, b, c):if n > 0:hanoi(n - 1, a, c, b)print("把%s移动到%s" % (a, c))hanoi(n - 1, b, a, c)hanoi(3, "A", "B", "C")# 结果：
把A移动到C
把A移动到B
把C移动到B
把A移动到C
把B移动到A
把B移动到C
把A移动到C