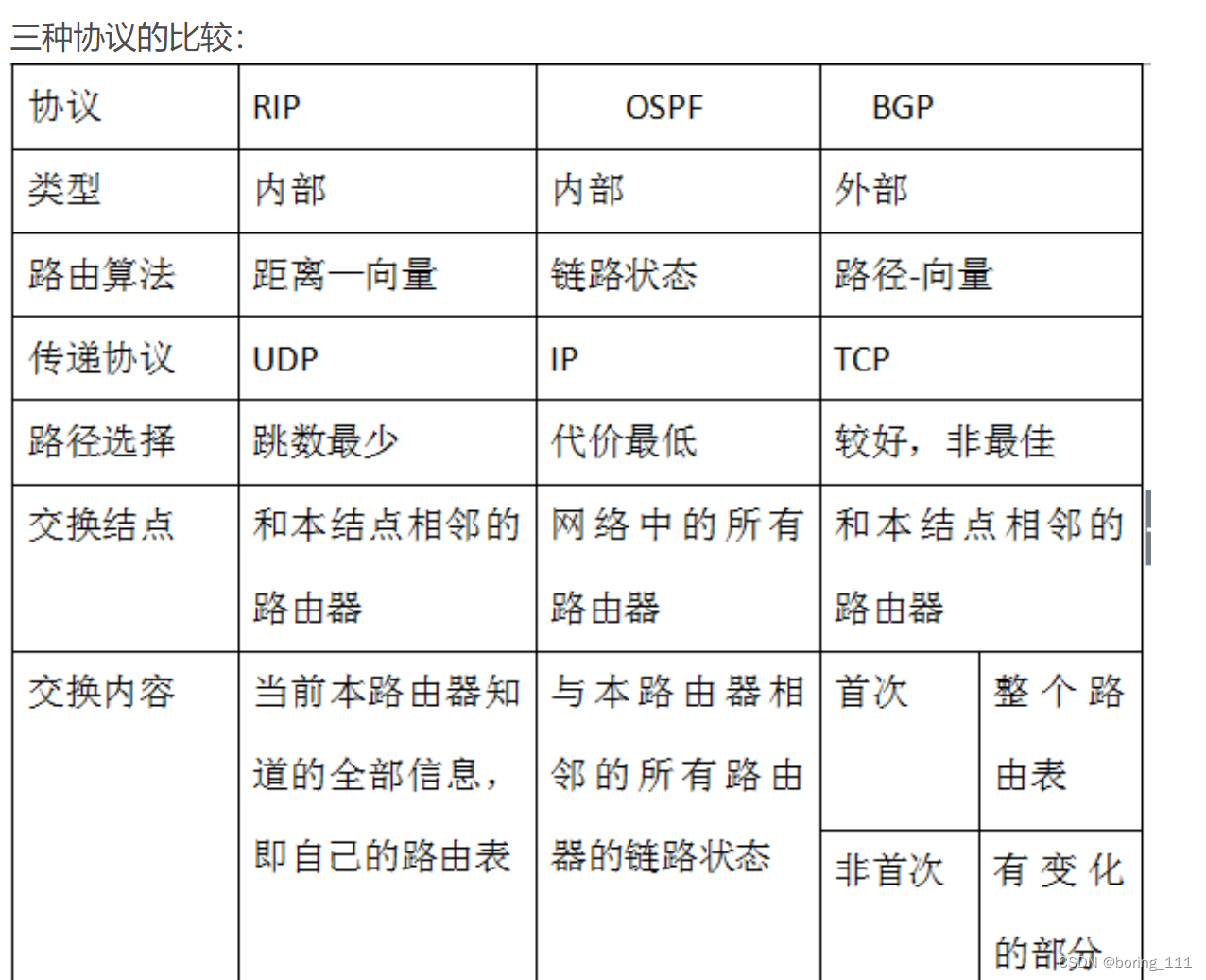
汉诺塔问题求解,在a杆上自上而下、由大到小顺序地串有64个盘子,要求把a杆上的盘子借助c杆全部移动到b杆上。
def hanoi(n,a,b,c):if(n>0):hanoi(n-1,a,c,b) #n-1个盘子,借助b杆放在c杆上print(“move disc no:{} from pile {} to {}”.format(n,a,b))#第n个盘子从a杆移动到b杆hanoi(n-1,c,b,a) #把c杆上的n-1个盘子借助a杆移动到b杆hanoi(64,’a’,’b’,’c’)科赫曲线的基本概念和绘制方法如下:
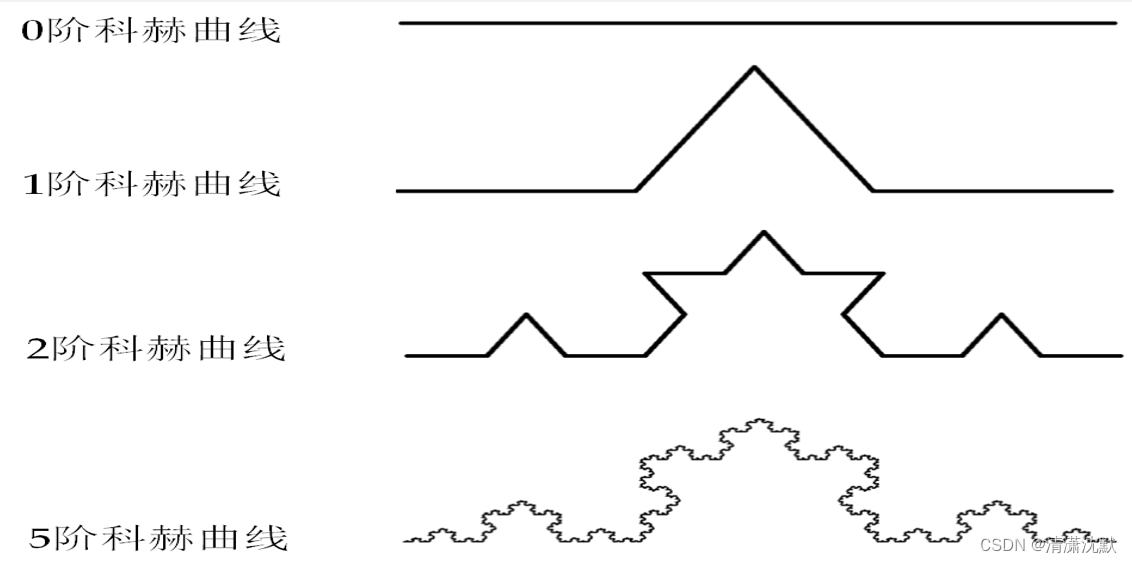
正整数n代表科赫曲线的阶数,表示生成科赫曲线过程的操作次数。科赫曲线初始化阶数为0,表示一个长度为L的直线。对于直线L,将其等分为三段,中间一段用边长为L/3的等边三角形的两个边替代,得到1阶科赫曲线,它包含四条线段。进一步对每条线段重复同样的操作后得到2阶科赫曲线。继续重复同样的操作n次可以得到n阶科赫曲线。
import turtle
def koch(size, n):if n == 0:turtle.fd(size)else:for angle in [0, 60, -120, 60]:turtle.left(angle)koch(size/3, n-1)
def main(n):turtle.setup(800,400) #启动图形窗口 800*400turtle.speed(0) #控制绘制速度turtle.penup() #让画笔抬起来,即不再在画布上留下轨迹,只是移动而已turtle.goto(-300, -50) ##将笔移动到-300,-50位置turtle.pendown() #放下笔turtle.pensize(2) #笔的粗度是2koch(600,n) #0阶科赫曲线长度,阶数 ,绘制长度为600,阶为n的雪花曲线turtle.hideturtle() #隐藏画笔的形状
main(3)#输入你想绘制的几阶科赫曲线科赫曲线的雪花效果:
import turtle
def koch(size, n):if n == 0:turtle.fd(size)else:for angle in [0, 60, -120, 60]:turtle.left(angle)koch(size/3, n-1)
def main():turtle.setup(600,600)turtle.speed(0)turtle.penup()turtle.goto(-200, 100)turtle.pendown()turtle.pensize(2)level = 5koch(400,level)turtle.right(120)koch(400,level)turtle.right(120)koch(400,level)turtle.hideturtle()
main()此节只为扩展,不做详解!!!