[LeetCode周赛复盘] 第 375 场周赛20231210
- 一、本周周赛总结
- 100143. 统计已测试设备
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 100155. 双模幂运算
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 100137. 统计最大元素出现至少 K 次的子数组
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 100136. 统计好分割方案的数目
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 参考链接
一、本周周赛总结
- T1 模拟。
- T2 快速幂模拟。
- T3 滑窗。
- T4 分组线段合并。
100143. 统计已测试设备
100143. 统计已测试设备
1. 题目描述
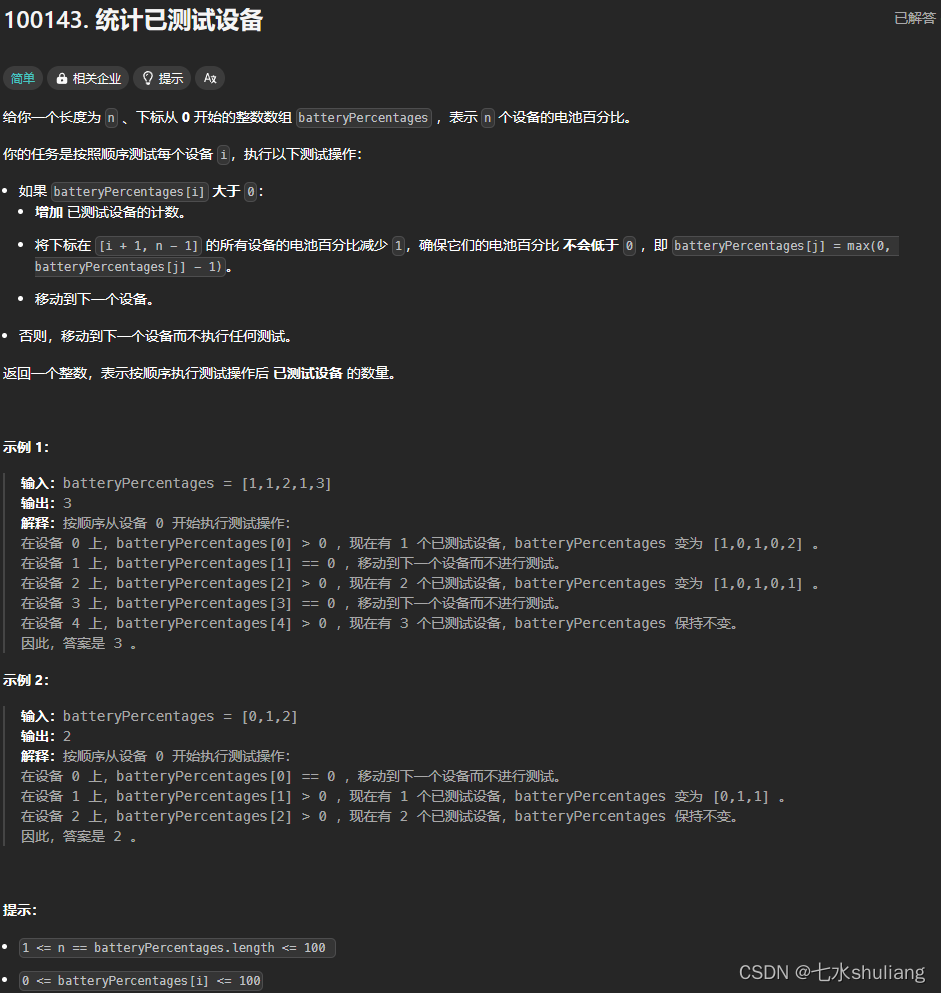
2. 思路分析
- 用一个d记录后边要减去的数量
3. 代码实现
class Solution:def countTestedDevices(self, batteryPercentages: List[int]) -> int: d = ans = 0for i in range(len(batteryPercentages)):if batteryPercentages[i] - d>0:ans += 1d += 1return ans
100155. 双模幂运算
100155. 双模幂运算
1. 题目描述
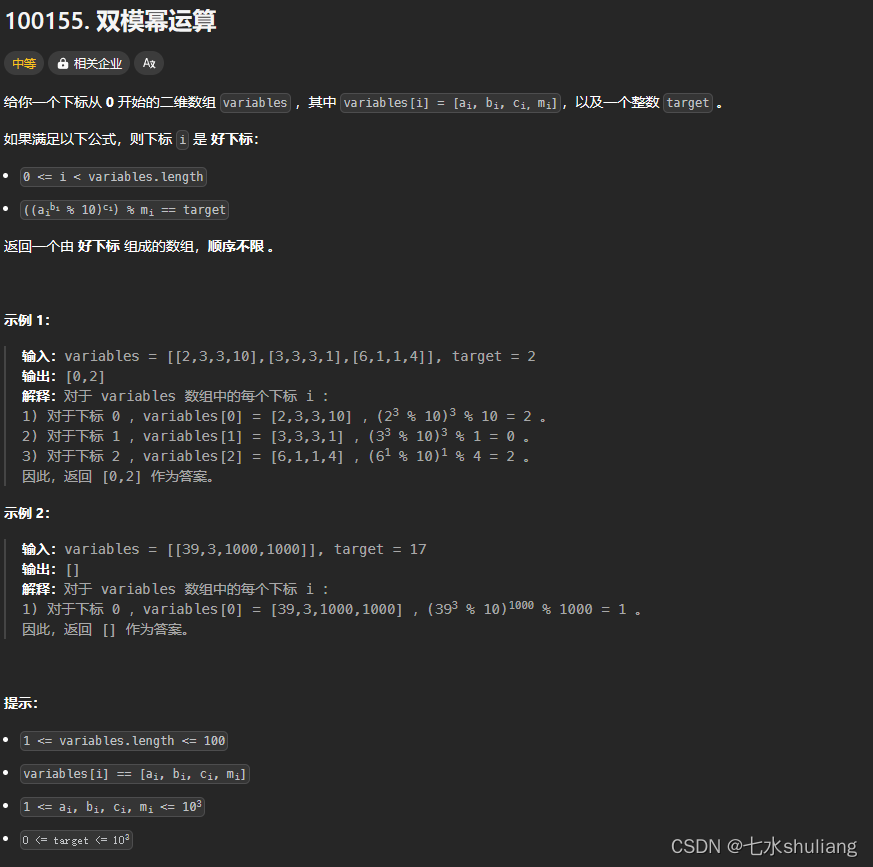
2. 思路分析
- 用py自带快速幂。
3. 代码实现
class Solution:def getGoodIndices(self, variables: List[List[int]], target: int) -> List[int]:return [i for i,(a,b,c,m) in enumerate(variables) if pow(pow(a,b,10),c,m) == target]
100137. 统计最大元素出现至少 K 次的子数组
100137. 统计最大元素出现至少 K 次的子数组
1. 题目描述
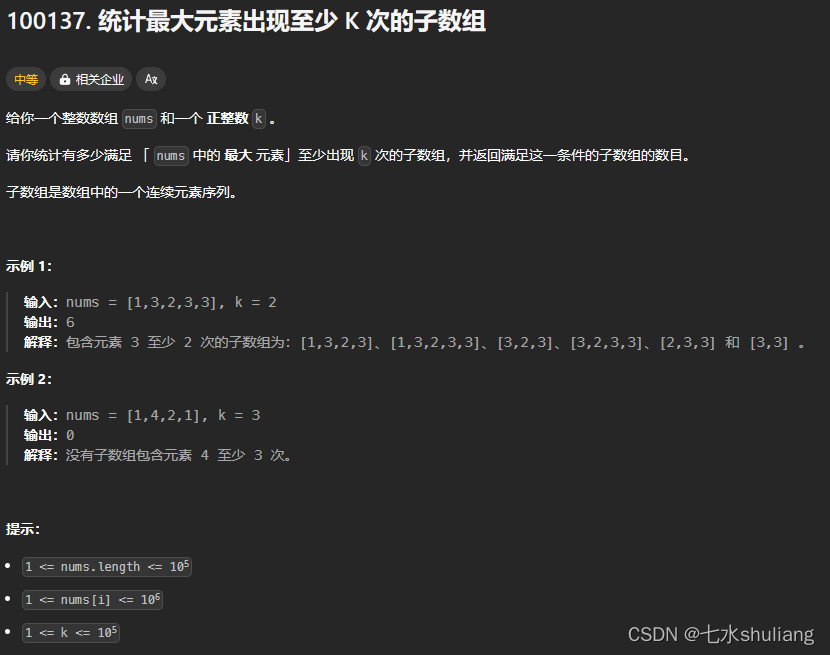
2. 思路分析
- 滑窗,但这题可能把窗口出到空,因此用双指针写法比队列写法方便一些。
- 对每个右端点,考虑左端点的个数,即左端点向左一下即能出现合法,因此当cnt[mx]>=k即可滑。
3. 代码实现
class Solution:def countSubarrays(self, nums: List[int], k: int) -> int:mx = max(nums)l = 0cnt = Counter()ans = 0 for i,v in enumerate(nums):cnt[v] += 1while cnt[mx] >= k:cnt[nums[l]] -= 1l += 1ans += lreturn ans
100136. 统计好分割方案的数目
100136. 统计好分割方案的数目
1. 题目描述
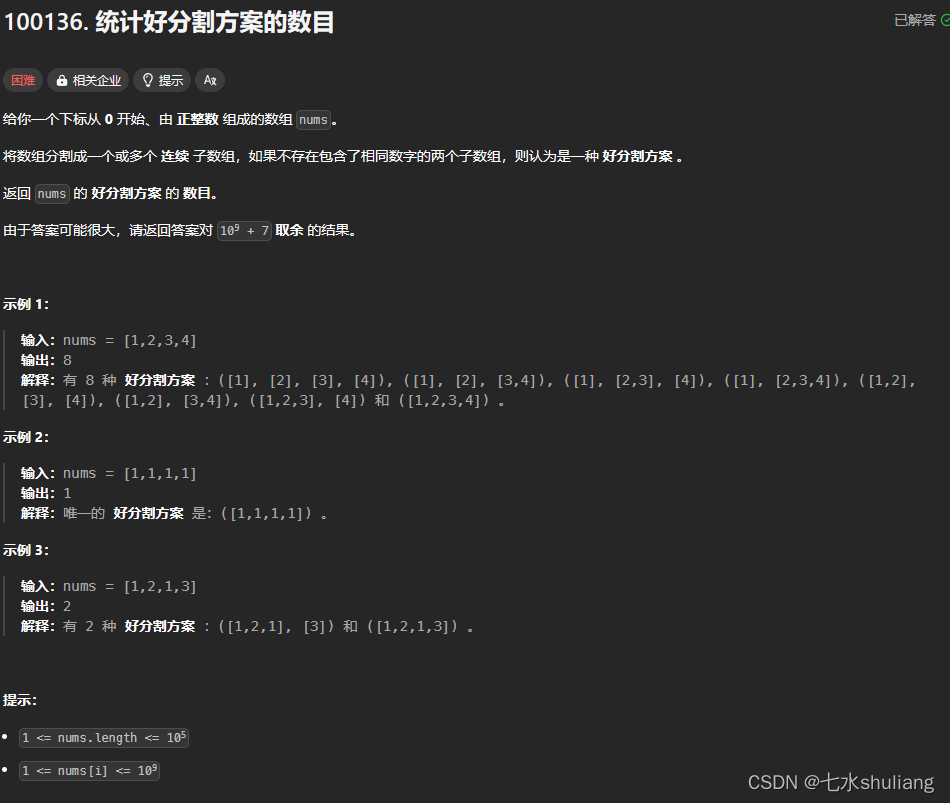
2. 思路分析
- 观察题意,要求相同数字必须分在同一组,因此可以先按数组分组,求每个数字的左右边界;
- 这时发现有的数字会有交叉,根据题意他们也应该同组。
- 于是想到线段合并。
- 合并完后,相邻组可以任意分组或者不分。那么方案数考虑插板,n组中间有n-1个位置,每个位置可以插或不插。
3. 代码实现
class Solution:def numberOfGoodPartitions(self, nums: List[int]) -> int:g = {}for i,v in enumerate(nums):if v not in g:g[v]= [i,0]g[v][1] = i lr = sorted(g.values())c = 1x,y = lr[0]for l,r in lr:if l > y:x = l c += 1y = max(y, r)return pow(2,c-1,10**9+7)


![[b01lers2020]Life on Mars 一个接口的sql schema.schemate表](https://img-blog.csdnimg.cn/direct/c773777fd95140f5b45b852b61879ef0.png)