题目描述
有M个小孩到公园玩,门票是1元。其中N个小孩带的钱为1元,K个小孩带的钱为2元。售票员没有零钱,问这些小孩共有多少种排队方法,使得售票员总能找得开零钱。注意:两个拿一元零钱的小孩,他们的位置互换,也算是一种新的排法。(M<=10)
输入格式
输入一行,M,N,K(其中M=N+K,M<=10).
输出格式
输出一行,总的排队方案。
样例输入
4 2 2
样例输出
8
方法一:
题目分析:
由题目可知,必须满足条件N>=K,拆分这个条件:
N=K
N个小孩带的钱为1元,另外N个小孩带的钱为2元,即2N=M,可以直接用卡特兰数:
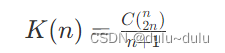
由于题目中说小孩交换位置算一种新的排队方式,所以还要再乘上 n 的全排列(乘两遍:N个小孩带的钱为1元,另外N个小孩带的钱为2元),即
N>K
先将非法的排列方法筛选出来,再用总的排列方法-非法的排列方法,得最终排列的方法数:
总的排列方法:
因为由M人,所以总的排列方法有M!种
非法的排列可以将其分为三个部分:
- 前 2P 个小孩
- 第 2P + 1 个小孩
- 剩下的小孩,假设共 R 个(R = M - 2P - 1)
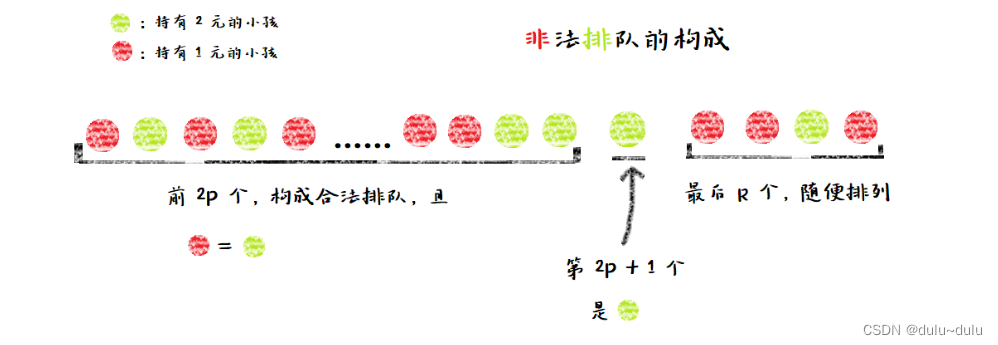
第一部分可以使用卡特兰公式进行运算,即,其中p在0~k范围内,但不能为K,因为第二部分必须为K中的一部分
其次,p可以为0,因为第二部分2p+1为持有2元的小孩,即第一个排队的人就是持有2元的小孩,也是非法的排列顺序:
由于第一部分已经用了k中的p个,第二部分有k-p个选择:
K-P
第三部分随意排列,即r=m-2*p-1进行随意排列:
R!
所以合法的排列公式为:
用代码实现即:
long long sum = 0;for (int p = 0; p <k; p++) {int r = m - 2 * p - 1;long long fail = catalan(p) * rank(k, p) * rank(n, p) * (k - p) * rank(r, r);sum += fail;}long long result = rank(m, m) - sum;printf("%lld\n", result);所以完整的代码得,如果其中有一些小漏洞,请大佬们不吝赐教!💖💖
#include<stdio.h>// 求排列数
long long rank(int a1, int a2) {if (a2 == 0) return 1;a2--;//这里一定不能忘记,因为要排除rank(c1,c2)中,c1为0得情况long long pro = a1;for (int i = 0; i < a2; i++) {a1--;pro *= a1;}return pro;
}// 求组合数
long long comb(int c1, int c2) {return rank(c1, c2) / rank(c2, c2);
}// 求卡特兰数
long long catalan(int n) {return comb(2 * n, n) / (n + 1);
}int main() {int m, n, k;scanf("%d %d %d", &m, &n, &k);if (n < k) {printf("Error: n must be greater than or equal to k.\n");return 0;}else {long long sum = 0;for (int p = 0; p <k; p++) {int r = m - 2 * p - 1;long long fail = catalan(p) * rank(k, p) * rank(n, p) * (k - p) * rank(r, r);sum += fail;}long long result = rank(m, m) - sum;printf("%lld\n", result);}return 0;
}方法二
我在网上也看到一种更简便得方法,在这里分享给大家,我的理解如下:
他利用了数据结构中的next_permutation(a,a+N)方法进行全排列,不熟悉的可以看这篇文章:
http://t.csdn.cn/TREc9
我们可以把它理解为序列的字典序的前后,严格来讲,就是对于当前序列pn,他的下一个序列pn+1满足:不存在另外的序列pm,使pn<pm<pn+1
正确的排列方法为:每个2前面至少对应着一个1
用一个num记录,num如果有1就++,有2就- - ,如果过程中num<0则证明存在有一个2没有一个1对应。
代码为:
这里初始前面的1为0~K-1,后面的2为K~N-1 所以小于K的就相当于是1了,大于K的就相当于是2了,为了方便使用next_permutation()
for (int i=0; i<K; i++) {a[i] = i;}for (int i=K; i<N; i++) {a[i] = i;}do {int flag = 0;// check每个全排列, num务必要初始化 int num = 0;for (int i=0; i<N; i++) {if (a[i] >= K) {num--;} else {num++;}if (num < 0) {flag = 1;break;}}if (flag == 0) {
// for (int i=0; i<N; i++) {
// cout << a[i];
// }
// cout << "\n";res++;}这还不够,需要判断类似1122的所有全排列包括重复的,因为初始前面的1为0~K-1,后面的2为K~N-1 ,对于0123的序列我们可以直接使用next_permutation(),完整代码如下:
#include <iostream>
#include <algorithm>
using namespace std;
int N, K, M;
int main() {while (cin >> N >> K >> M) {int a[N], res = 0;for (int i=0; i<K; i++) {a[i] = i;}for (int i=K; i<N; i++) {a[i] = i;}do {int flag = 0;// check每个全排列, num务必要初始化 int num = 0;for (int i=0; i<N; i++) {if (a[i] >= K) {num--;} else {num++;}if (num < 0) {flag = 1;break;}}if (flag == 0) {
// for (int i=0; i<N; i++) {
// cout << a[i];
// }
// cout << "\n";res++;}} while (next_permutation(a,a+N));cout << res << "\n";}return 0;
}