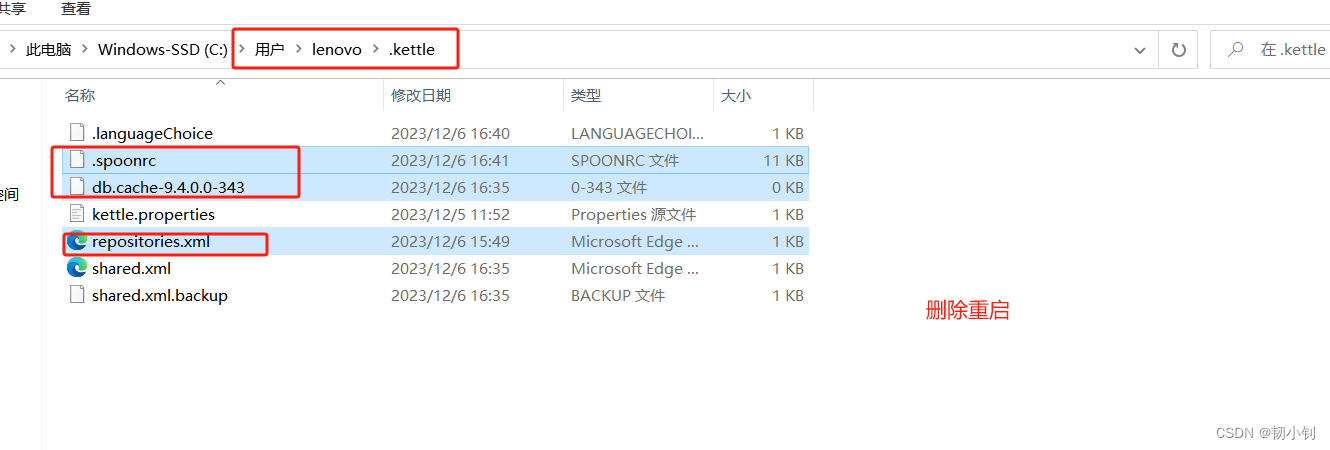
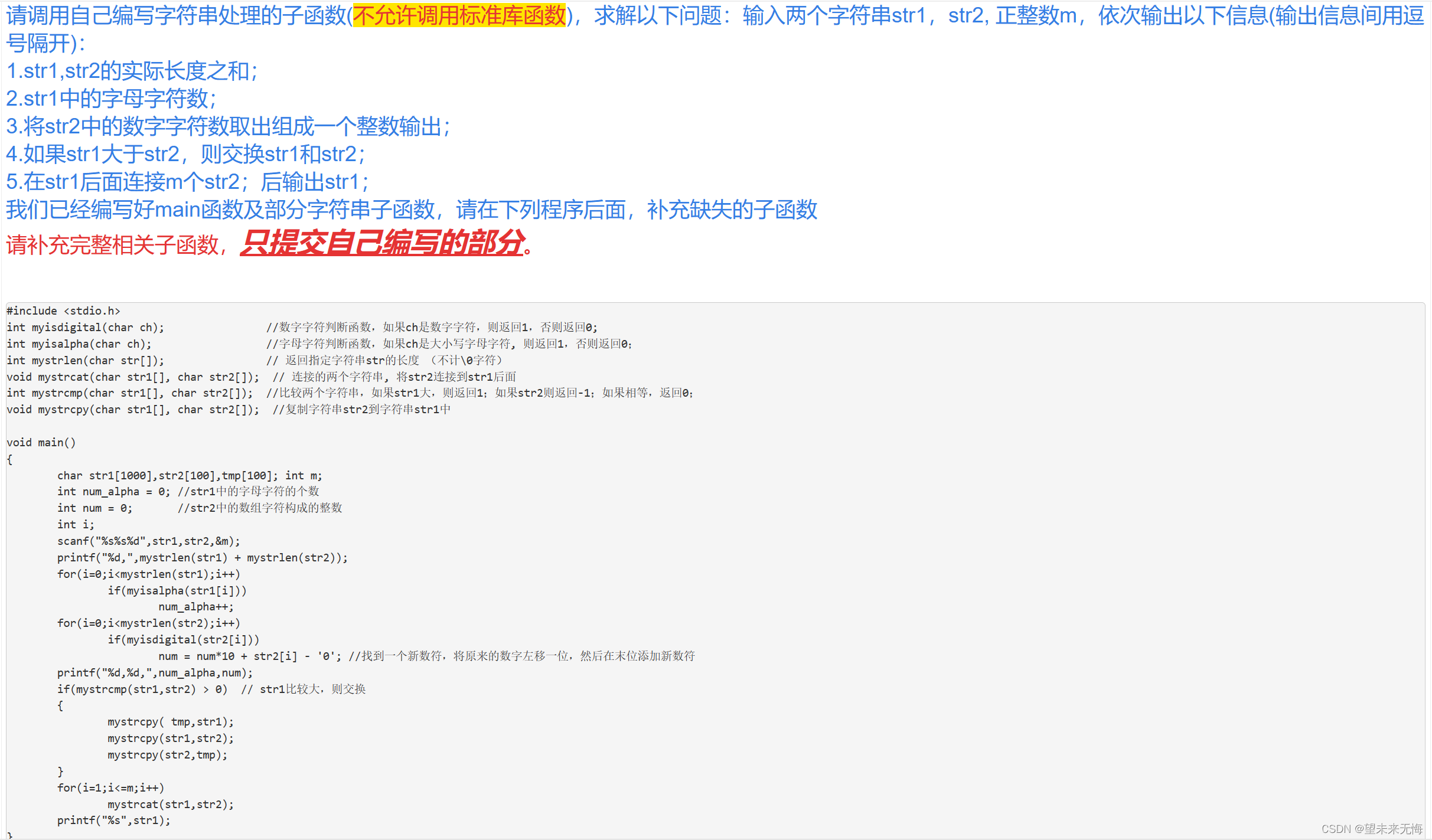
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
> 示例 1:
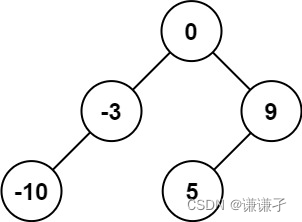
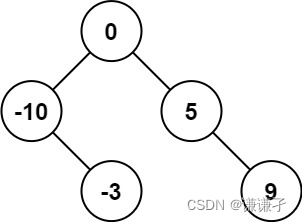
输入:nums = [-10,-3,0,5,9] 输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
> 示例 2:
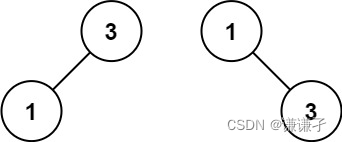
输入:nums = [1,3] 输出:[3,1] 解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
提示:
1 <= nums.length <= 104
-104 <= nums[i] <= 104 nums 按 严格递增 顺序排列
方法一:中序遍历,总是选择中间位置左边的数字作为根节点 选择中间位置左边的数字作为根节点,则根节点的下标为
mid=(left+right)/2\textit{mid}=(\textit{left}+\textit{right})/2mid=(left+right)/2,此处的除法为整数除法。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode sortedArrayToBST(int[] nums) {return HeightBalenced(nums,0,nums.length - 1);}public TreeNode HeightBalenced(int[] nums, int left, int right){if(left > right){return null;}//总是选择中间位置左边的数字作为根节点int mid = (left + right) / 2;TreeNode root = new TreeNode(nums[mid]);root.left = HeightBalenced(nums,left,mid - 1);root.right = HeightBalenced(nums,mid + 1,right);return root;}
}
复杂度分析
时间复杂度:O(n),其中 n是数组的长度。每个数字只访问一次。
空间复杂度:O(logn),其中 n 是数组的长度。空间复杂度不考虑返回值,因此空间复杂度主要取决于递归栈的深度,递归栈的深度是 O(logn)。
方法二:中序遍历,总是选择中间位置右边的数字作为根节点
选择中间位置右边的数字作为根节点,则根节点的下标为 mid=(left+right+1)/2\textit{mid}=(\textit{left}+\textit{right}+1)/2mid=(left+right+1)/2,此处的除法为整数除法。
class Solution {public TreeNode sortedArrayToBST(int[] nums) {return helper(nums, 0, nums.length - 1);}public TreeNode helper(int[] nums, int left, int right) {if (left > right) {return null;}// 总是选择中间位置右边的数字作为根节点int mid = (left + right + 1) / 2;TreeNode root = new TreeNode(nums[mid]);root.left = helper(nums, left, mid - 1);root.right = helper(nums, mid + 1, right);return root;}
}
复杂度分析
时间复杂度:O(n),其中 n 是数组的长度。每个数字只访问一次。
空间复杂度:O(logn),其中 n 是数组的长度。空间复杂度不考虑返回值,因此空间复杂度主要取决于递归栈的深度,递归栈的深度是 O(logn)
方法三:中序遍历,选择任意一个中间位置数字作为根节点
选择任意一个中间位置数字作为根节点,则根节点的下标为 mid=(left+right)/2\textit{mid}=(\textit{left}+\textit{right})/2mid=(left+right)/2 和 mid=(left+right+1)/2\textit{mid}=(\textit{left}+\textit{right}+1)/2mid=(left+right+1)/2 两者中随机选择一个,此处的除法为整数除法。
class Solution {Random rand = new Random();public TreeNode sortedArrayToBST(int[] nums) {return helper(nums, 0, nums.length - 1);}public TreeNode helper(int[] nums, int left, int right) {if (left > right) {return null;}// 选择任意一个中间位置数字作为根节点int mid = (left + right + rand.nextInt(2)) / 2;TreeNode root = new TreeNode(nums[mid]);root.left = helper(nums, left, mid - 1);root.right = helper(nums, mid + 1, right);return root;}
}
复杂度分析
时间复杂度:O(n),其中 n 是数组的长度。每个数字只访问一次。
空间复杂度:O(logn),其中 n 是数组的长度。空间复杂度不考虑返回值,因此空间复杂度主要取决于递归栈的深度,递归栈的深度是 O(logn)