DS二叉排序树之删除-编程知识

Description

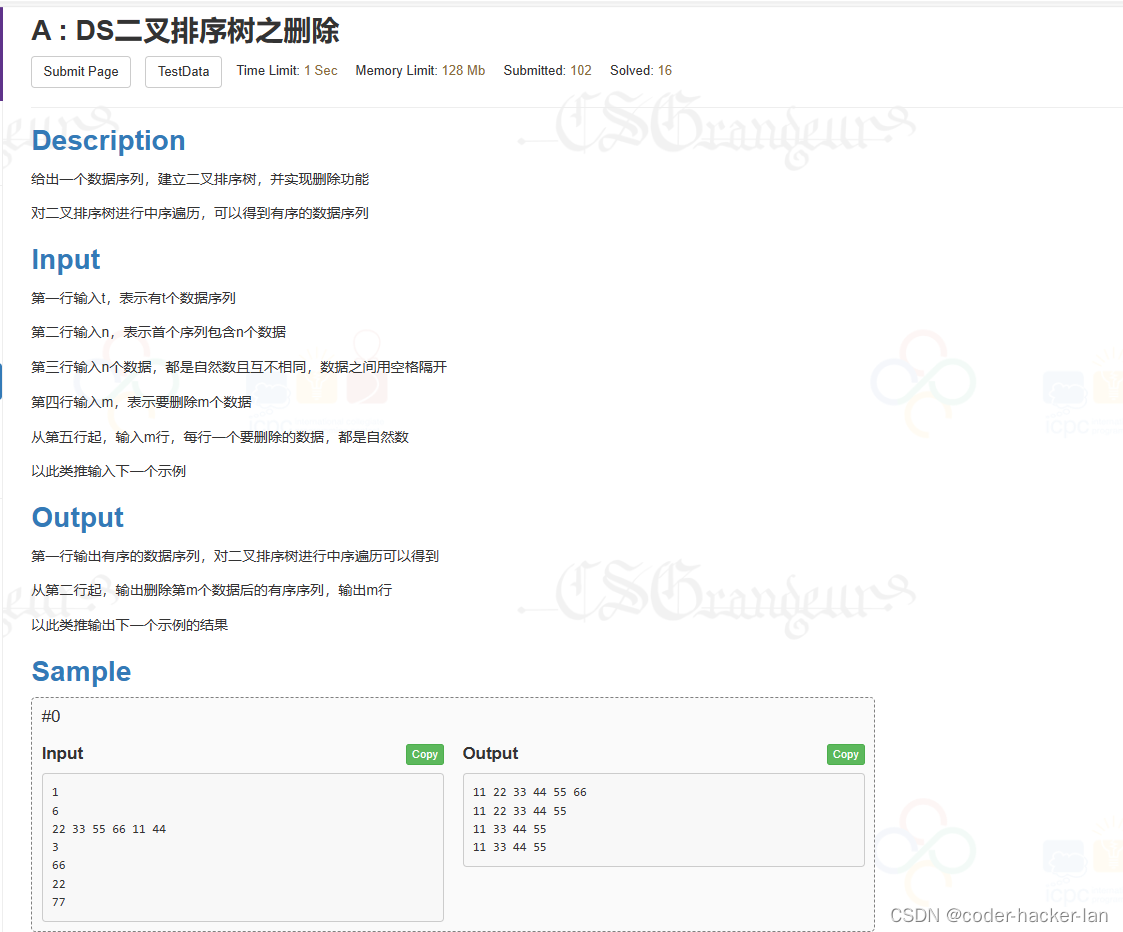
给出一个数据序列，建立二叉排序树，并实现删除功能

对二叉排序树进行中序遍历，可以得到有序的数据序列

Input

第一行输入t，表示有t个数据序列

第二行输入n，表示首个序列包含n个数据

第三行输入n个数据，都是自然数且互不相同，数据之间用空格隔开

第四行输入m，表示要删除m个数据

从第五行起，输入m行，每行一个要删除的数据，都是自然数

以此类推输入下一个示例

Output

第一行输出有序的数据序列，对二叉排序树进行中序遍历可以得到

从第二行起，输出删除第m个数据后的有序序列，输出m行

以此类推输出下一个示例的结果

Sample

Input

Copy

1
6
22 33 55 66 11 44
3
66
22
77

Output

Copy

11 22 33 44 55 66 
11 22 33 44 55 
11 33 44 55 
11 33 44 55

难点：

1.普通的删除：删除的是叶子

2.删除的是中间的节点但是只有左右子树其中一个

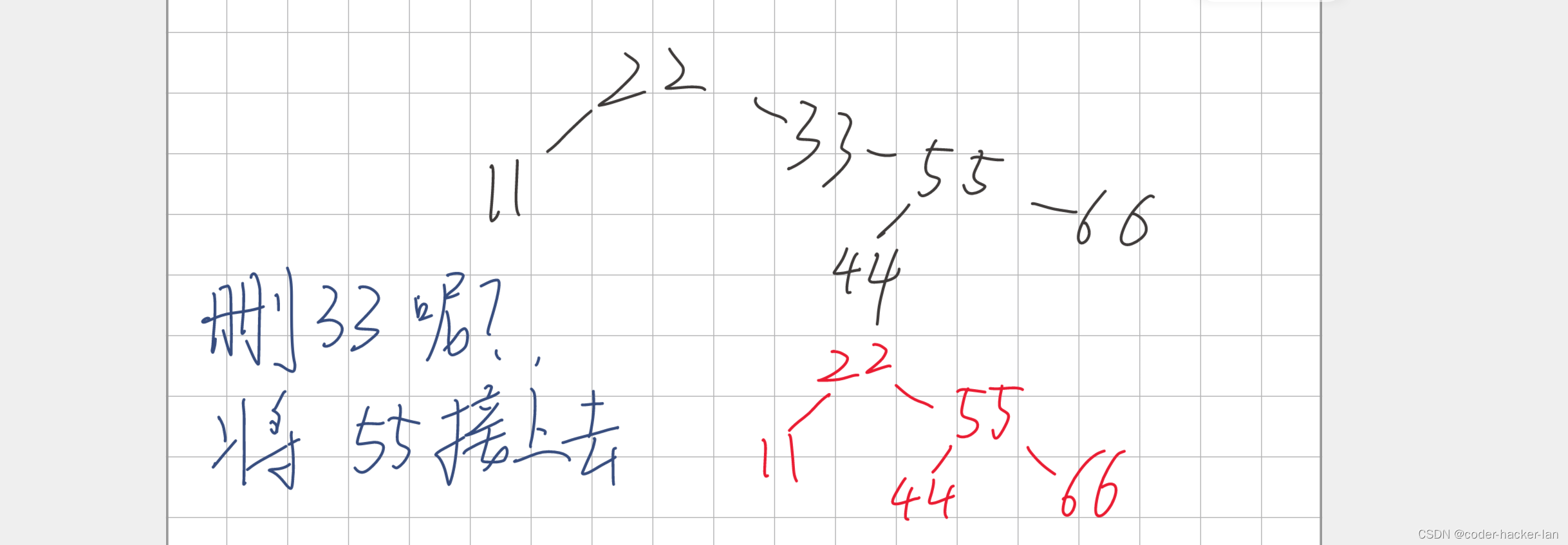
3.删除的节点是中间的节点且左右子树都有值

思路：

1.删除的是叶子

直接把那个叶子删了，不要了，就是这么大气！！！

2.删除的是中间的节点，但是只有左右子树其中一个

直接将要删掉的他的子树接上去就好了

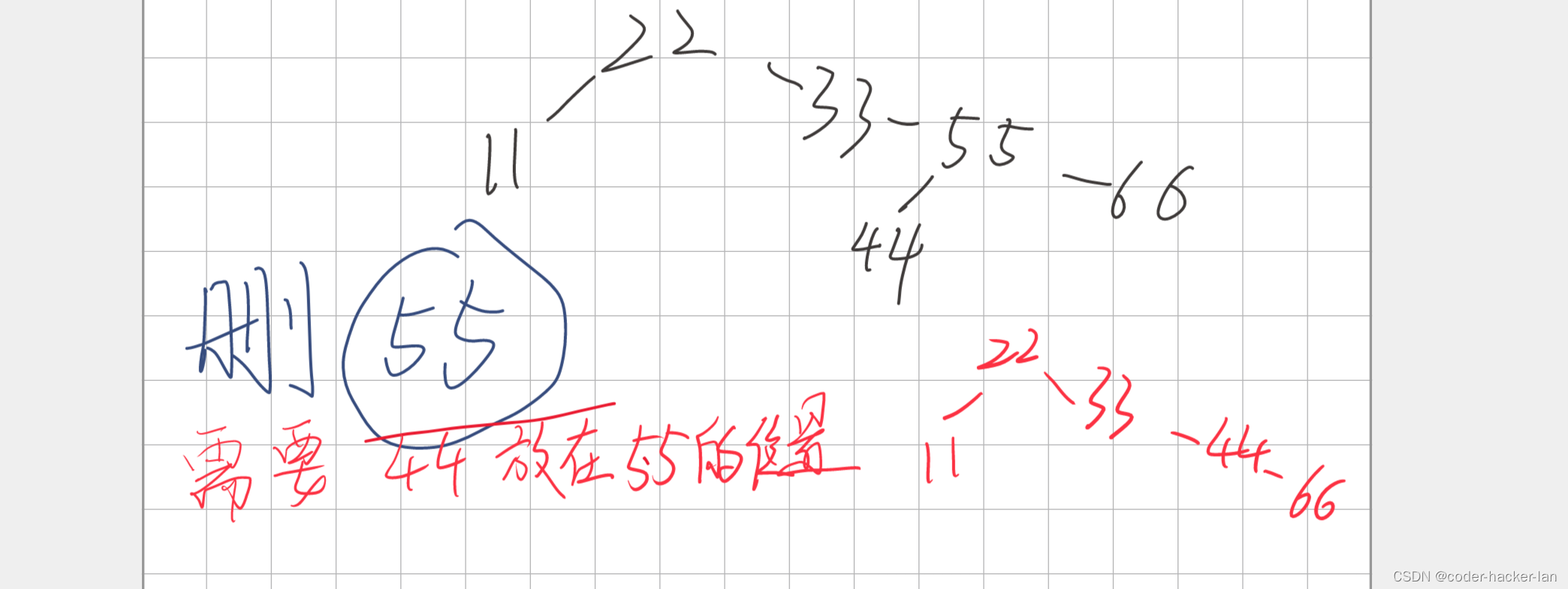
3.要删的节点左右子树都有值

我给此时的树再加一点，有点突然，别介意
分为两种情况

1.这个要删的节点22的左子树11只有左子树15没有右子树，

2.要删的节点22的左子树11不只有一个左子树还有右子树

tips：
1.为什么要找左子树最大值？
因为二叉排序树左子树小于根，根小于右子树，所以找左子树最大一直向右找就行了
2.为什么20的左子树是不是null没有关系？
因为我们只需要拿20替换22的位置，花圈部分再比20小，也是11的右子树的位置里，肯定比11大，所以11的右子树直接指向花圈部分没有问题

删除节点的的部分：

分为三个部分

1.删除的节点左子树为空，那就直接把这个节点的右子树接上去
2.删除的节点右子树为空，那就直接把这个节点的左子树接上去
3.删除的节点左右子树不为空：
root为要被删除的节点
一：root的左子树只有一个左子树，那就把这个节点替换要删的节点的值，然后root的左指针指向被替换节点的左子树，对应这张图

二：左子树不只有一个节点，那就找这个子树的最大值，跟要删的节点替换，且这个节点的父节点的右指针指向最大值的左子树，对应这张图

代码部分：

1.构建二叉排序树，可以参考我另一篇文章DS二叉排序树之查找

结构体：

建立根：

剩下的元素逐个插入：

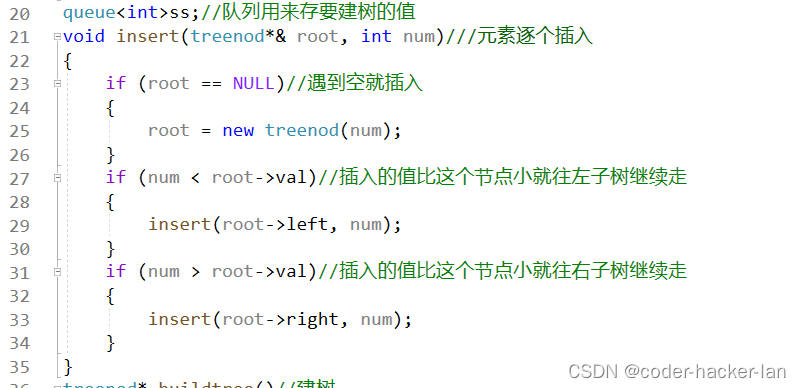
2.删除元素的函数

找到要删除的元素的节点的位置

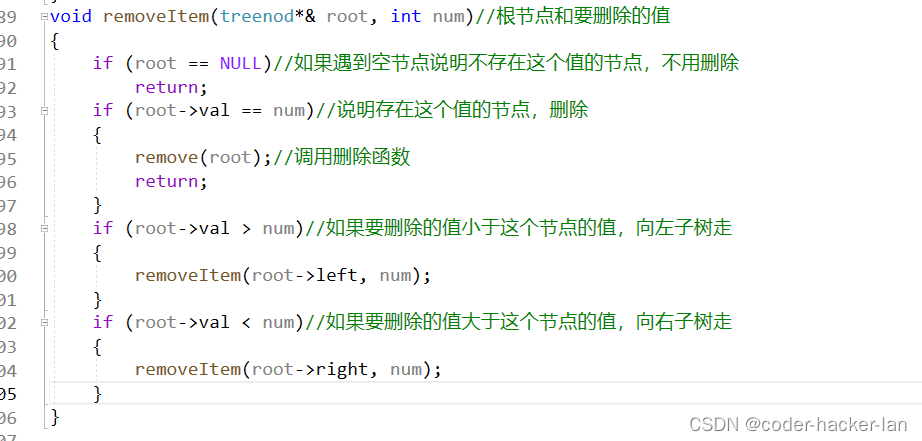
删除函数remove

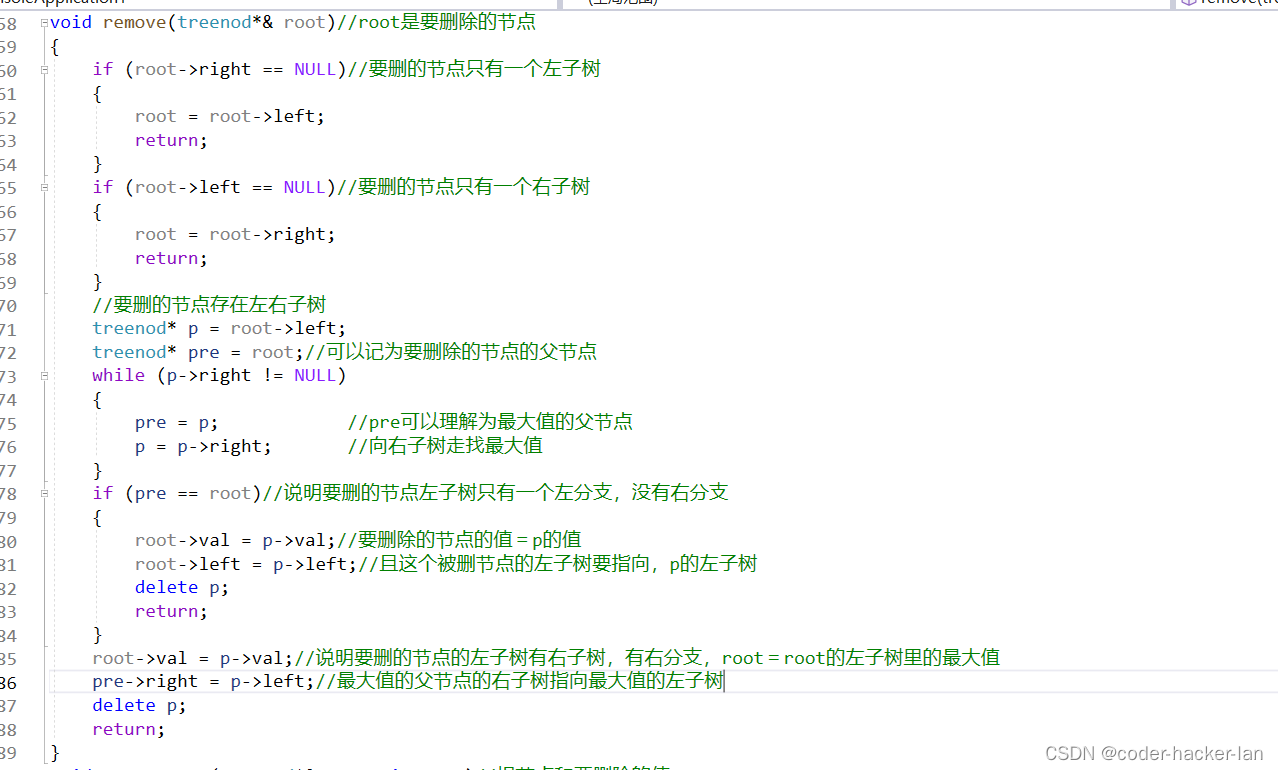
完整代码：

#include <iostream>
#include <queue>
using namespace std;
struct treenod
{int val;treenod* left, * right;//左右子树指针treenod(){left = NULL;right = NULL;}treenod(int x){val = x;left = NULL;right = NULL;}
};
queue<int>ss;//队列用来存要建树的值
void insert(treenod*& root, int num)///元素逐个插入
{if (root == NULL)//遇到空就插入{root = new treenod(num);}if (num < root->val)//插入的值比这个节点小就往左子树继续走{insert(root->left, num);}if (num > root->val)//插入的值比这个节点小就往右子树继续走{insert(root->right, num);}
}
treenod* buildtree()//建树
{if (ss.empty())return NULL;treenod* root;root = new treenod(ss.front());//先建立根ss.pop();while (!ss.empty()){insert(root, ss.front());//剩下的元素都一个一个插入ss.pop();}return root;
}
void zhonxu(treenod* root)
{if (root == NULL)return;zhonxu(root->left);cout << root->val << " ";zhonxu(root->right);
}
void remove(treenod*& root)//root是要删除的节点
{if (root->right == NULL)//要删的节点只有一个左子树{root = root->left;return;}if (root->left == NULL)//要删的节点只有一个右子树{root = root->right;return;}//要删的节点存在左右子树treenod* p = root->left;treenod* pre = root;//可以记为要删除的节点的父节点while (p->right != NULL){pre = p;            //pre可以理解为最大值的父节点p = p->right;       //向右子树走找最大值}if (pre == root)//说明要删的节点左子树只有一个左分支，没有右分支{root->val = p->val;//要删除的节点的值＝p的值root->left = p->left;//且这个被删节点的左子树要指向，p的左子树delete p;return;}root->val = p->val;//说明要删的节点的左子树有右子树，有右分支，root＝root的左子树里的最大值pre->right = p->left;//最大值的父节点的右子树指向最大值的左子树delete p;return;
}
void removeItem(treenod*& root, int num)//根节点和要删除的值
{if (root == NULL)//如果遇到空节点说明不存在这个值的节点，不用删除return;if (root->val == num)//说明存在这个值的节点，删除{remove(root);//调用删除函数return;}if (root->val > num)//如果要删除的值小于这个节点的值，向左子树走{removeItem(root->left, num);}if (root->val < num)//如果要删除的值大于这个节点的值，向右子树走{removeItem(root->right, num);}
}int main()
{int t;cin >> t;while (t--){int n;cin >> n;for (int i = 1; i <= n; i++){int num;cin >> num;ss.push(num);}treenod* root;root = buildtree();zhonxu(root);cout << endl;int m;cin >> m;for (int i = 1; i <= m; i++){int num;cin >> num;removeItem(root, num);zhonxu(root);cout << endl;}}return 0;
}

偷懒下，主函数不想打注释了，也不长，有读题的都知道在干嘛

这周估计就更这个吧，因为要备考四级了，而且我也不是大佬，后面的题还不太会，等我慢慢学吧！！！
不要催更，不要催更，不要催更！！！
祝我四级不要再421分好吧有缘人。

我祝你六级轻松拿下600分！！！