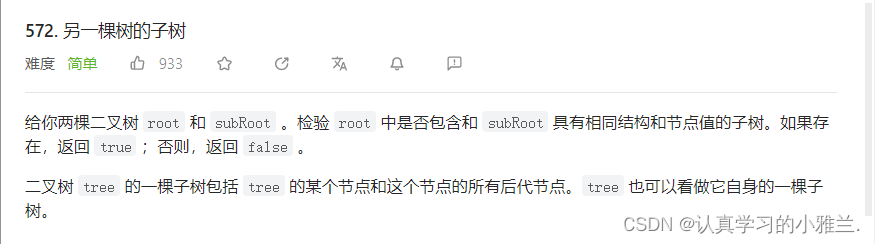
二叉树（下）+Leetcode每日一题——“数据结构与算法”“对称二叉树”“另一棵树的子树”“二叉树的前中后序遍历”

各位CSDN的uu们你们好呀，今天小雅兰的内容仍然是二叉树和Leetcode每日一题，下面，就让我们进入二叉树的世界吧！！！

 

 

这个题目需要重新定义一个函数，函数参数需要有左子树和右子树，题目所给定的函数无法解决问题。

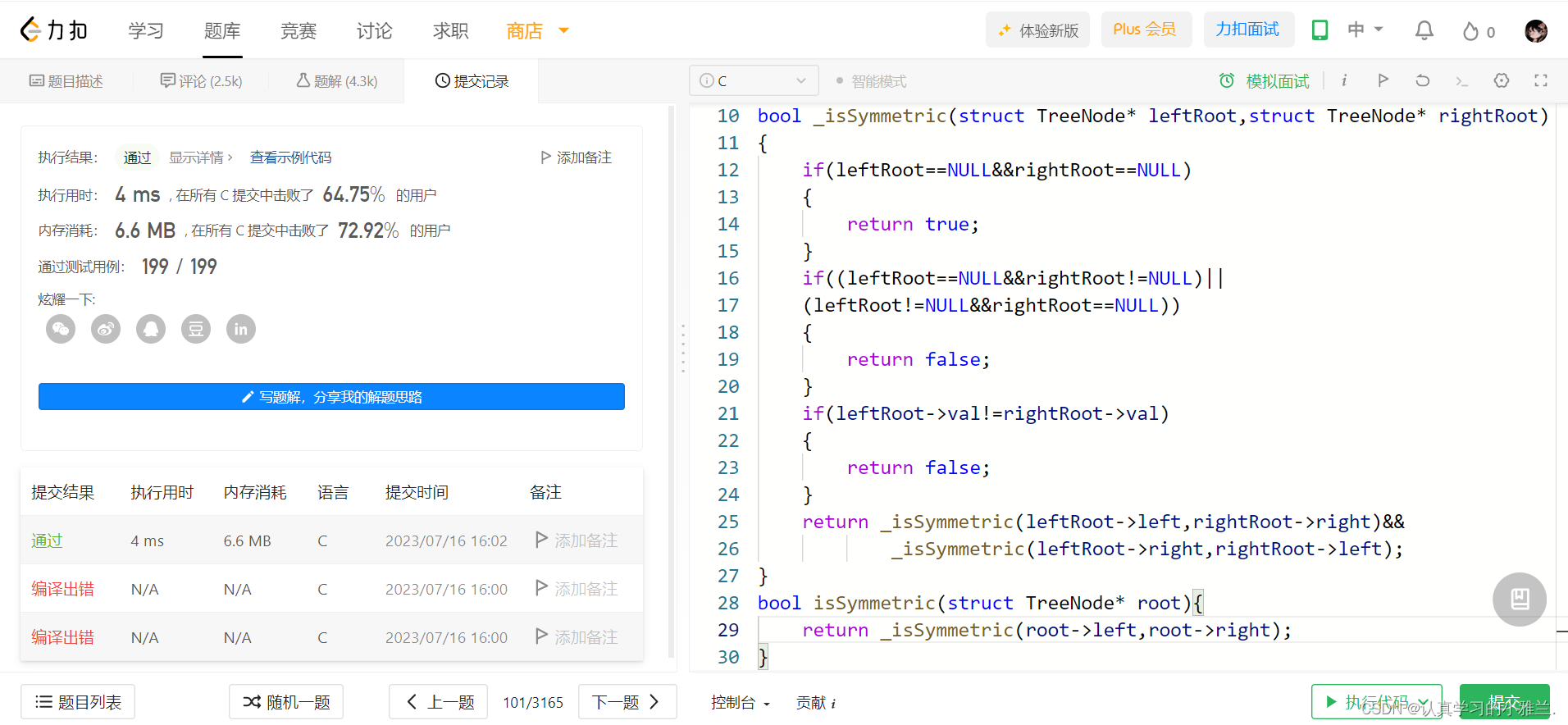
bool _isSymmetric(struct TreeNode* leftRoot,struct TreeNode* rightRoot)
{//左子树和右子树同时为空if(leftRoot==NULL&&rightRoot==NULL){return true;}//一棵树为空，另一棵树不为空if((leftRoot==NULL&&rightRoot!=NULL)||(leftRoot!=NULL&&rightRoot==NULL)){return false;}//左子树的根和右子树的根不相等//这就必然不对称if(leftRoot->val!=rightRoot->val){return false;}return _isSymmetric(leftRoot->left,rightRoot->right)&&_isSymmetric(leftRoot->right,rightRoot->left);
}
bool isSymmetric(struct TreeNode* root){return _isSymmetric(root->left,root->right);
}

 

 

 

 

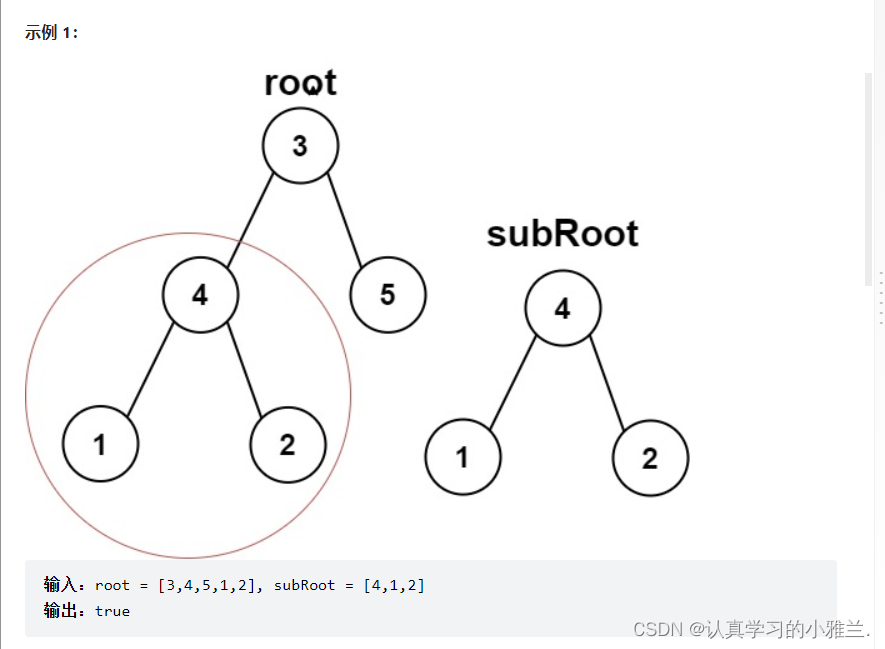
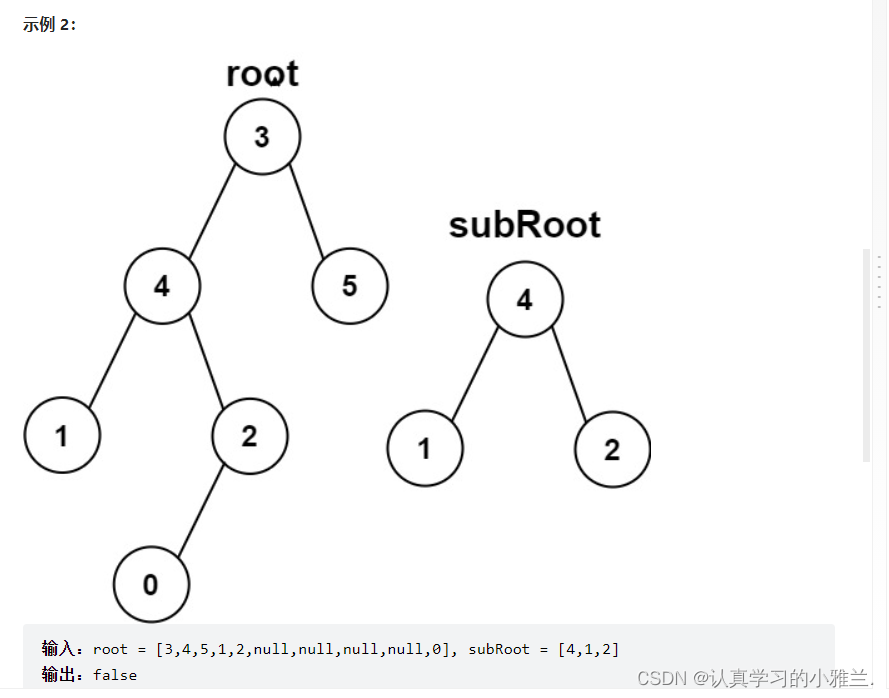
每个不为空的结点，都可以认为是一棵子树的根 

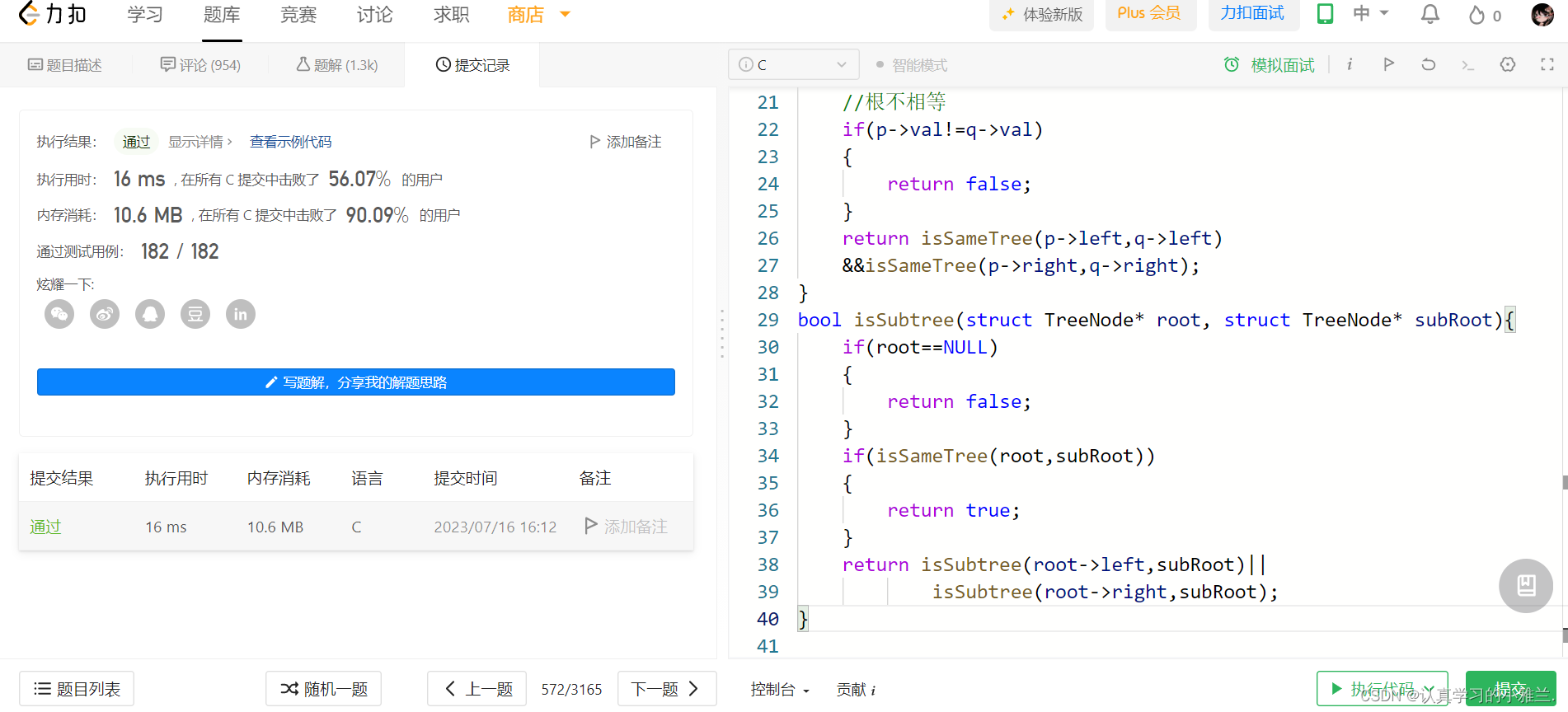
//两棵树相同
bool isSameTree(struct TreeNode* p, struct TreeNode* q){//两个都为空if(p==NULL&&q==NULL){return true;}//一个为空，另一个不为空if((p==NULL&&q!=NULL)||(p!=NULL&&q==NULL)){return false;}//根不相等if(p->val!=q->val){return false;}return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){if(root==NULL){return false;}//root和subRoot相同if(isSameTree(root,subRoot)){return true;}//root的左子树与subRoot有相同或者root的右子树与subRoot有相同//满足其中一个条件即可，所以用||return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
}

 

 

 

 

递归里面传数组下标要注意！！！

每个栈帧里面都有一个数组下标！！！ 

所以要传数组下标的地址。

int TreeSize(struct TreeNode* root)
{return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;
}
//递归里面传数组下标要注意！！！
//每个栈帧里面都有一个i
void preorder(struct TreeNode* root,int* a,int* pi)
{if(root==NULL){return;}a[(*pi)++]=root->val;preorder(root->left,a,pi);preorder(root->right,a,pi);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){//root是输入型参数，returnSize是返回型参数*returnSize=TreeSize(root);int* a=(int*)malloc(*returnSize*sizeof(int));int i=0;preorder(root,a,&i);return a;
}

 

 

当然，这个题目还有另外一种解法，就是把i作为全局变量，但是这样要特别注意，稍有不慎就会出错

int TreeSize(struct TreeNode* root)

{

    return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;

}

//递归里面传数组下标要注意！！！

//每个栈帧里面都有一个i

int i=0;

void preorder(struct TreeNode* root,int* a)

{

    if(root==NULL)

    {

        return;

    }

    a[i++]=root->val;

    preorder(root->left,a);

    preorder(root->right,a);

}

int* preorderTraversal(struct TreeNode* root, int* returnSize){

    //root是输入型参数，returnSize是返回型参数

    *returnSize=TreeSize(root);

    int* a=(int*)malloc(*returnSize*sizeof(int));

    i=0;

    preorder(root,a);

    return a;

}

 

int TreeSize(struct TreeNode* root)

{

    return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;

}

void inorder(struct TreeNode* root,int* a,int* pi)

{

    if(root==NULL)

    {

        return;

    }

    inorder(root->left,a,pi);

    a[(*pi)++]=root->val;

    inorder(root->right,a,pi);

}

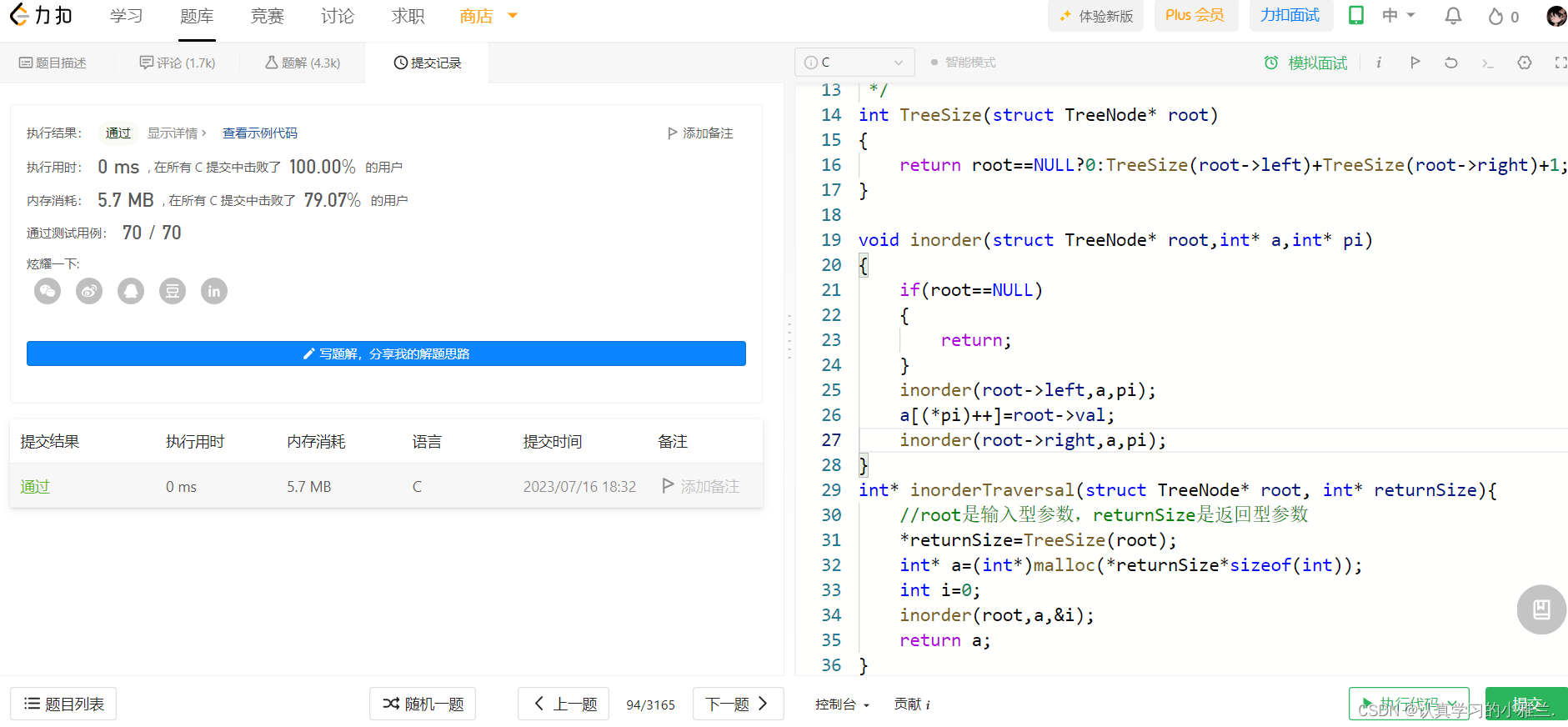
int* inorderTraversal(struct TreeNode* root, int* returnSize){

    //root是输入型参数，returnSize是返回型参数

    *returnSize=TreeSize(root);

    int* a=(int*)malloc(*returnSize*sizeof(int));

    int i=0;

    inorder(root,a,&i);

    return a;

}

 

 

int TreeSize(struct TreeNode* root)

{

    return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;

}

void postorder(struct TreeNode* root,int* a,int* pi)

{

    if(root==NULL)

    {

        return;

    }

    postorder(root->left,a,pi);

    postorder(root->right,a,pi);

     a[(*pi)++]=root->val;

}

int* postorderTraversal(struct TreeNode* root, int* returnSize){

    //root是输入型参数，returnSize是返回型参数

    *returnSize=TreeSize(root);

    int* a=(int*)malloc(*returnSize*sizeof(int));

    int i=0;

    postorder(root,a,&i);

    return a;

}

 

 

层序遍历

除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层 上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。

 

1出来带2和4，2出来带3和NULL，4出来带和6 

写这个代码的核心是得有一个队列！！！

Queue.h的内容：

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
typedef struct BinaryTreeNode* QDataType;
// 链式结构：表示队列 
typedef struct QueueNode
{struct QueueNode* next;QDataType data;
}QueueNode;
// 队列的结构 
typedef struct Queue
{QueueNode* phead;//头指针QueueNode* ptail;//尾指针int size;
}Queue;
// 初始化队列
void QueueInit(Queue* pq);// 销毁队列 
void QueueDestroy(Queue* pq);// 队尾入队列 
void QueuePush(Queue* pq, QDataType x);// 队头出队列 
void QueuePop(Queue* pq);// 获取队列头部元素 
QDataType QueueFront(Queue* pq);// 获取队列队尾元素 
QDataType QueueBack(Queue* pq);// 获取队列中有效元素个数 
int QueueSize(Queue* pq);// 检测队列是否为空
bool QueueEmpty(Queue* pq);

Queue.c的内容：

#include"Queue.h"
// 初始化队列
void QueueInit(Queue* pq)
{assert(pq);pq->phead = NULL;pq->ptail = NULL;pq->size = 0;
}
// 销毁队列 
void QueueDestroy(Queue* pq)
{assert(pq);QueueNode* cur = pq->phead;while (cur != NULL){QueueNode* next = cur->next;free(cur);cur = next;}pq->phead = pq->ptail = NULL;pq->size = 0;
}
// 队尾入队列 
void QueuePush(Queue* pq, QDataType x)
{assert(pq);QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));if (newnode == NULL){perror("malloc fail");return;}newnode->data = x;newnode->next = NULL;//是空队列的情况if (pq->ptail == NULL){assert(pq->phead == NULL);pq->phead = pq->ptail = newnode;}else{pq->ptail->next = newnode;pq->ptail = newnode;}pq->size++;
}
// 检测队列是否为空
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->phead == NULL && pq->ptail == NULL;
}
// 队头出队列 
void QueuePop(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));//1.一个结点//2.多个结点if (pq->phead->next == NULL){free(pq->phead);pq->phead = pq->ptail = NULL;}else{//相当于头删QueueNode* next = pq->phead->next;free(pq->phead);pq->phead = next;}pq->size--;
}
// 获取队列头部元素 
QDataType QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->phead->data;
}// 获取队列队尾元素 
QDataType QueueBack(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->ptail->data;
}// 获取队列中有效元素个数 
int QueueSize(Queue* pq)
{assert(pq);return pq->size;
}

层序遍历源代码：

//层序遍历
void LevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root != NULL){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->data);if (front->left != NULL){QueuePush(&q, front->left);}if (front->right != NULL){QueuePush(&q, front->right);}}printf("\n");QueueDestroy(&q);
}

 

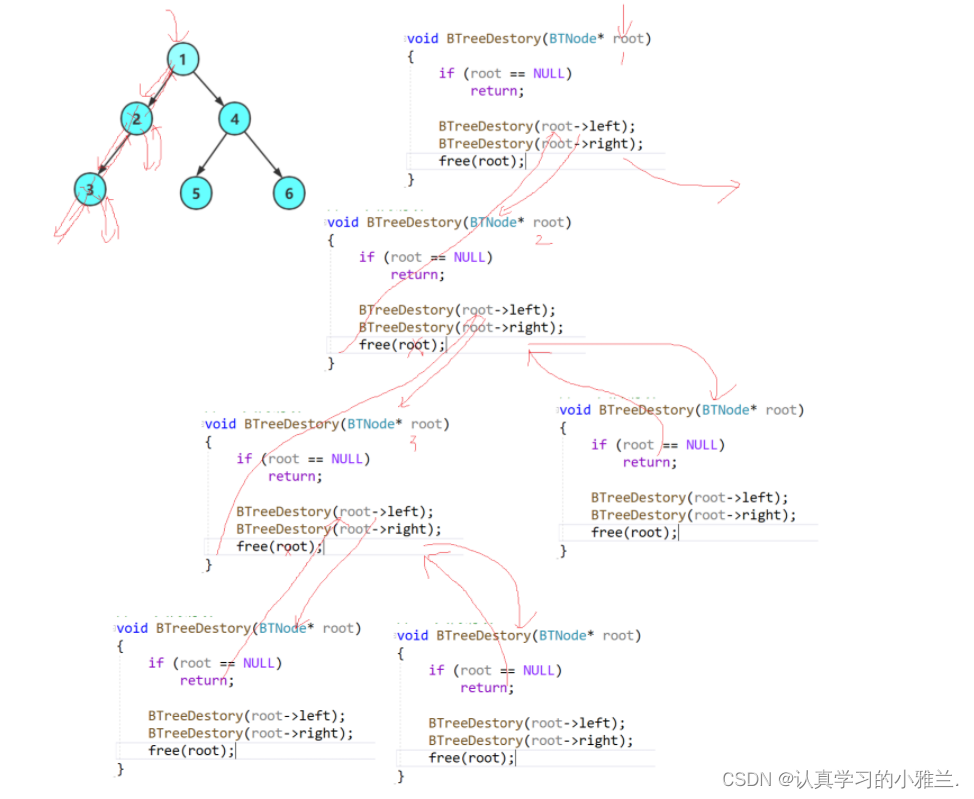
二叉树销毁

//二叉树销毁
void BTreeDestroy(BTNode* root)
{if (root == NULL){return;}BTreeDestroy(root->left);BTreeDestroy(root->right);free(root);
}

 

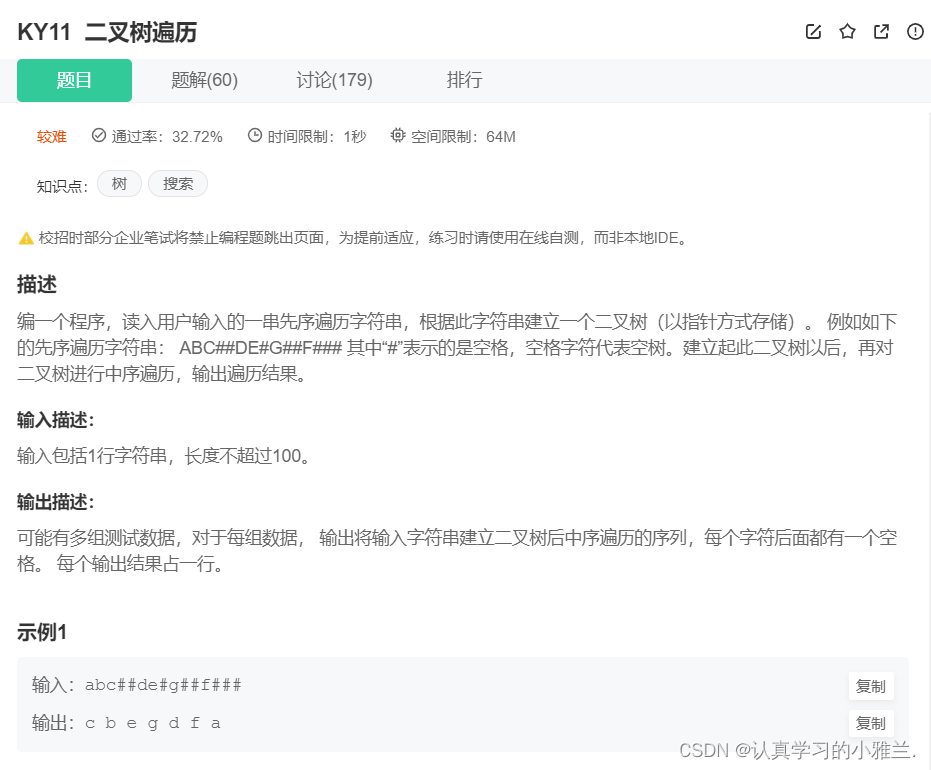
通 过 前 序 遍 历 的 数 组 " A B D # # E # H # # C F # # G # # " 构 建 二 叉 树

根        左子树        右子树

 

#include <stdio.h>
#include<stdlib.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;BTNode* BuyNode(BTDataType x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");return NULL;}node->data = x;node->left = NULL;node->right = NULL;return node;
}
BTNode* CreatTree(char* a,int* pi)
{if(a[*pi]=='#'){(*pi)++;return NULL;}BTNode* root=BuyNode(a[*pi]);(*pi)++;root->left=CreatTree(a,pi);root->right=CreatTree(a,pi);return root;
}
//中序
void InOrder(BTNode* root)
{if (root == NULL){return;}InOrder(root->left);printf("%c ", root->data);InOrder(root->right);
}
int main()
{char a[100];scanf("%s",a);int i=0;BTNode*root=CreatTree(a,&i);InOrder(root);printf("\n");return 0;}

 

 

 

判断二叉树是否是完全二叉树

完全二叉树的特征是：层序遍历去走，它是连续的！！！

 

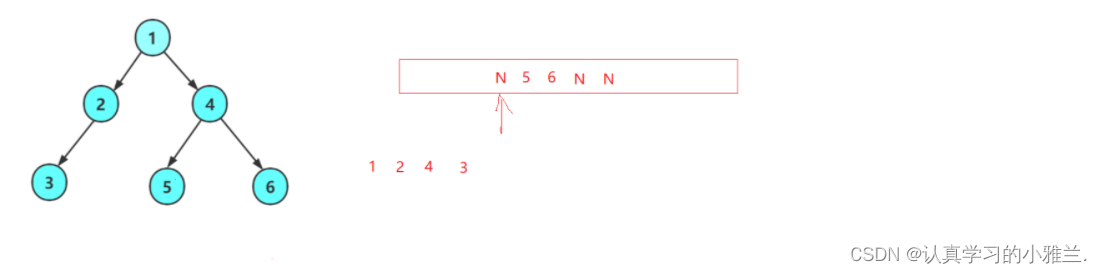
1出来带2和4，2出来带3和NULL，4出来带5和6，3出来带NULL和NULL，但是，3后面的NULL的后面竟然还有非空，这就证明此树是一棵非完全二叉树。

 

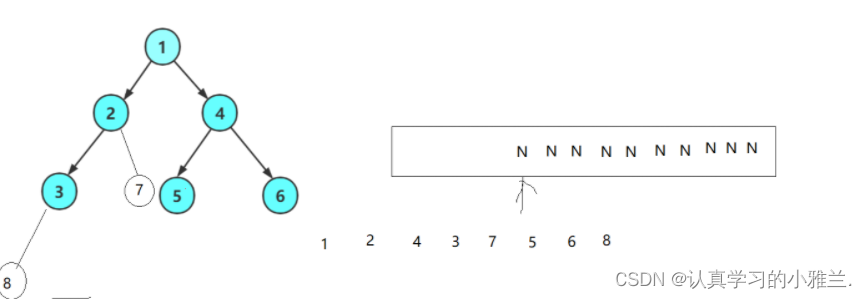
1出来带2和4，2出来带3和7，4出来带5和6，3出来带8和NULL，7出来带NULL和NULL，5出来带NULL和NULL，6出来带NULL和NULL，8出来带NULL和NULL，也就是说，队列里面的全都是空了，这一定是一棵完全二叉树。

//判断二叉树是否是完全二叉树
bool BTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root != NULL){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);//遇到空就跳出循环if (front == NULL){break;}QueuePush(&q, front->left);QueuePush(&q, front->right);}//检查后面的结点有没有非空//有非空，就不是完全二叉树while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front != NULL){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}

 

1.某完全二叉树按层次输出（同一层从左到右）的序列为 ABCDEFGH 。该完全二叉树的前序序列为（ A ）

A ABDHECFG

B ABCDEFGH

C HDBEAFCG

D HDEBFGCA

2.二叉树的先序遍历和中序遍历如下：先序遍历：EFHIGJK;中序遍历：HFIEJKG.则二叉树根结点为（ A ）

A E

B F

C G

D H

此题与中序遍历无关（中序遍历是迷惑人的），光看先序遍历就可以看出来，先序遍历就是根        左子树        右子树，所以E就是根结点。

但如果是想还原出这棵二叉树，中序遍历就很重要啦！！！

 

3.设一棵二叉树的中序遍历序列：badce，后序遍历序列：bdeca，则二叉树前序遍历序列为（ D ）。

A adbce

B decab

C debac

D abcde

后序遍历序列最后一个是a,所以a就是根节点！！！

4.某二叉树的后序遍历序列与中序遍历序列相同，均为 ABCDEF ，则按层次输出（同一层从左到右）的序列为（ A ）

A FEDCBA

B CBAFED

C DEFCBA

D ABCDEF

二叉树的性质

 

 

整个二叉树的源代码：

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include"Queue.h"
typedef int BTDataType;
typedef struct BinaryTreeNode
{
    BTDataType data;
    struct BinaryTreeNode* left;
    struct BinaryTreeNode* right;
}BTNode;

BTNode* BuyNode(BTDataType x)
{
    BTNode* node = (BTNode*)malloc(sizeof(BTNode));
    if (node == NULL)
    {
        perror("malloc fail");
        return NULL;
    }
    node->data = x;
    node->left = NULL;
    node->right = NULL;
    return node;
}

BTNode* CreatBinaryTree()
{
    BTNode* node1 = BuyNode(1);
    BTNode* node2 = BuyNode(2);
    BTNode* node3 = BuyNode(3);
    BTNode* node4 = BuyNode(4);
    BTNode* node5 = BuyNode(5);
    BTNode* node6 = BuyNode(6);

    node1->left = node2;
    node1->right = node4;
    node2->left = node3;
    node4->left = node5;
    node4->right = node6;
    return node1;
}

//前序
void PrevOrder(BTNode* root)
{
    if (root == NULL)
    {
        printf("NULL ");
        return;
    }
    printf("%d ", root->data);
    PrevOrder(root->left);
    PrevOrder(root->right);
}

//中序
void InOrder(BTNode* root)
{
    if (root == NULL)
    {
        printf("NULL ");
        return;
    }
    InOrder(root->left);
    printf("%d ", root->data);
    InOrder(root->right);
}

//后序
void PostOrder(BTNode* root)
{
    if (root == NULL)
    {
        printf("NULL ");
        return;
    }
    PostOrder(root->left);
    PostOrder(root->right);
    printf("%d ", root->data);
}
 

二叉树结点个数
//int size = 0;//全局变量
//int BTreeSize(BTNode* root)
//{
//    if (root == NULL)
//    {
//        return;
//    }
//    else
//    {
//        ++size;
//    }
//    BTreeSize(root->left);
//    BTreeSize(root->right);
//}
二叉树结点个数
//int BTreeSize(BTNode* root)
//{
//    if (root == NULL)
//    {
//        return 0;
//    }
//    else
//    {
//        return BTreeSize(root->left) + BTreeSize(root->right) + 1;
//    }
//}


//二叉树结点个数
int BTreeSize(BTNode* root)
{
    return root == NULL ? 0 : BTreeSize(root->left) + BTreeSize(root->right) + 1;
}


//求叶子结点的个数
int BTreeleafSize(BTNode* root)
{
    if (root == NULL)
    {
        return 0;
    }
    if (root->left == NULL && root->right == NULL)
    {
        return 1;
    }
    return BTreeleafSize(root->left) + BTreeleafSize(root->right);
}

//求二叉树的高度
int BTreeHeight(BTNode* root)
{
    if (root == NULL)
    {
        return 0;
    }
    else
    {
        int leftHeight = BTreeHeight(root->left);
        int rightHeight = BTreeHeight(root->right);
        return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
    }
}


// 二叉树第k层节点个数
int BTreeLevelKSize(BTNode* root, int k)
{
    assert(k > 0);
    if (root == NULL)//无论k是多少
    {
        return 0;
    }
    //root一定不为空
    if (k == 1)
    {
        return 1;
    }
    //root不为空并且k不为1
    return BTreeLevelKSize(root->left, k - 1) + BTreeLevelKSize(root->right, k - 1);
}


// 二叉树查找值为x的节点
BTNode* BTreeFind(BTNode* root, BTDataType x)
{
    if (root == NULL)
    {
        return NULL;
    }
    if (root->data == x)
    {
        return root;
    }
    BTNode* ret1 = BTreeFind(root->left, x);
    if (ret1)
    {
        return ret1;
    }
    BTNode* ret2 = BTreeFind(root->right, x);
    if (ret2)
    {
        return ret2;
    }
    return NULL;
}


//层序遍历
void LevelOrder(BTNode* root)
{
    Queue q;
    QueueInit(&q);
    if (root != NULL)
    {
        QueuePush(&q, root);
    }
    while (!QueueEmpty(&q))
    {
        BTNode* front = QueueFront(&q);
        QueuePop(&q);
        printf("%d ", front->data);
        if (front->left != NULL)
        {
            QueuePush(&q, front->left);
        }
        if (front->right != NULL)
        {
            QueuePush(&q, front->right);
        }
    }
    printf("\n");
    QueueDestroy(&q);
}


//二叉树销毁
void BTreeDestroy(BTNode* root)
{
    if (root == NULL)
    {
        return;
    }
    BTreeDestroy(root->left);
    BTreeDestroy(root->right);
    free(root);
}


//判断二叉树是否是完全二叉树
bool BTreeComplete(BTNode* root)
{
    Queue q;
    QueueInit(&q);
    if (root != NULL)
    {
        QueuePush(&q, root);
    }
    while (!QueueEmpty(&q))
    {
        BTNode* front = QueueFront(&q);
        QueuePop(&q);
        //遇到空就跳出循环
        if (front == NULL)
        {
            break;
        }
        QueuePush(&q, front->left);
        QueuePush(&q, front->right);
    }
    //检查后面的结点有没有非空
    //有非空，就不是完全二叉树
    while (!QueueEmpty(&q))
    {
        BTNode* front = QueueFront(&q);
        QueuePop(&q);
        if (front != NULL)
        {
            QueueDestroy(&q);
            return false;
        }
    }
    QueueDestroy(&q);
    return true;
}

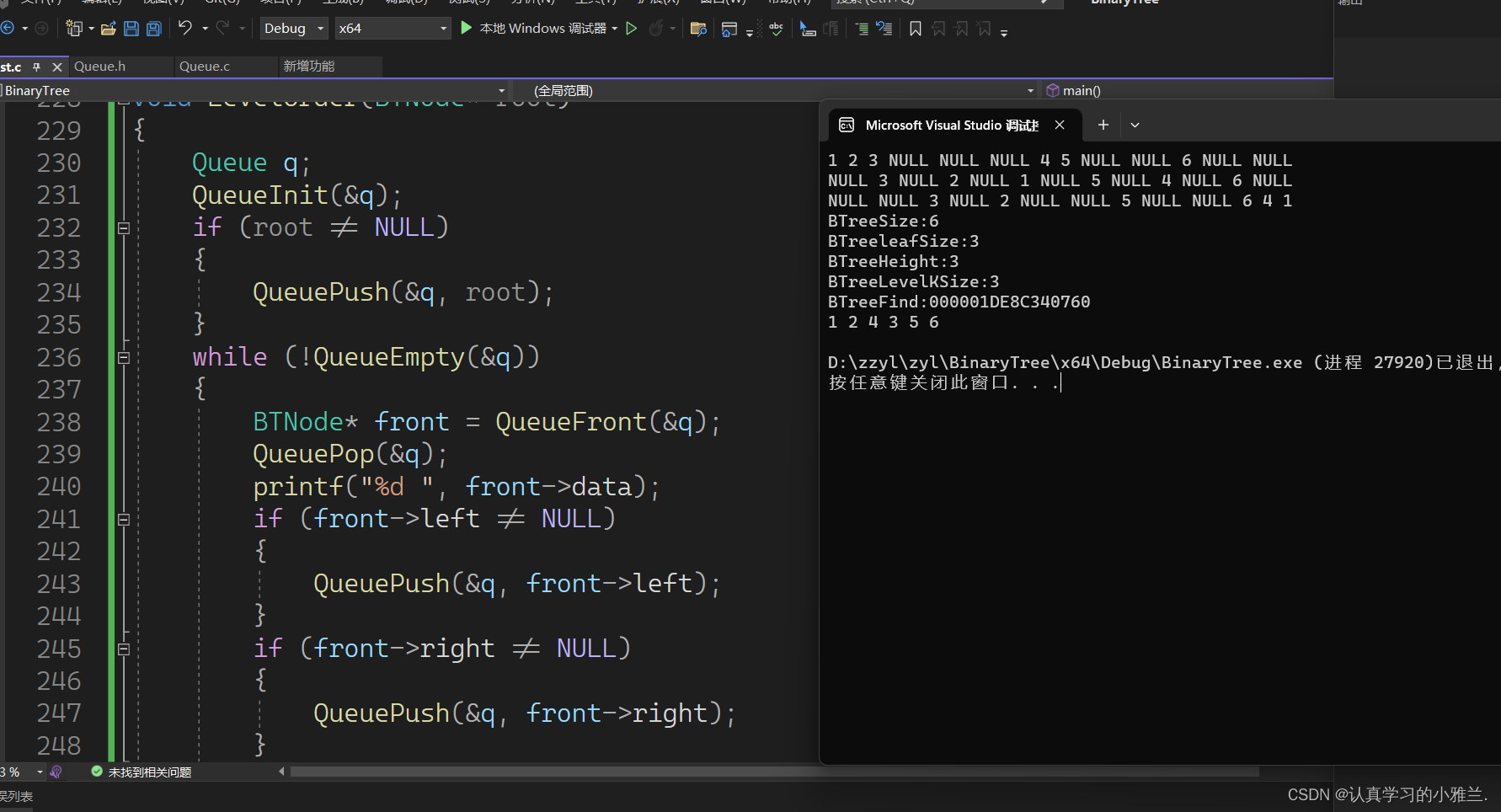
int main()
{
    BTNode* root = CreatBinaryTree();
    PrevOrder(root);
    printf("\n");

    InOrder(root);
    printf("\n");

    PostOrder(root);
    printf("\n");

    /*BTreeSize(root);
    printf("BTreeSize:%d\n", size);

    size = 0;
    BTreeSize(root);
    printf("BTreeSize:%d\n", size);

    size = 0;
    BTreeSize(root);
    printf("BTreeSize:%d\n", size);*/

    printf("BTreeSize:%d\n",BTreeSize(root));

    printf("BTreeleafSize:%d\n", BTreeleafSize(root));

    printf("BTreeHeight:%d\n", BTreeHeight(root));

    printf("BTreeLevelKSize:%d\n", BTreeLevelKSize(root, 3));

    printf("BTreeFind:%p\n", BTreeFind(root, 3));

    LevelOrder(root);

    BTreeDestroy(root);
    root = NULL;

    return 0;
}
 

好啦，小雅兰的今日分享就到这里啦，还要继续加油学习噢！！！

 

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/26954.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

cesium的使用

cesium的使用

cesium的使用 cesium的使用创建一个vue项目 vuevitecesium参数的使用常用点位标记删除动态渲染路线借助truf.js的算法进行渲染地块的实现topojson cesium的使用 1.下载或者安装cesium的插件 官方文档 下载下来后创建文件夹整个包引入 2.生成token 新的包应该有默认token如果没…
阅读更多...
【idea】的一些使用指南

【idea】的一些使用指南

一、serializable自动生成id 1.打开File菜单&#xff0c;选择Settings选项 2.打开Editor->Inspections 3.在右边的搜索框中输入serialVersionUID关键字&#xff0c;出现以下选项&#xff0c;勾选"Serializable class without serialVersionUID"&#xff0c;然后别…
阅读更多...
MySQL-概述-数据模型SQL简介

MySQL-概述-数据模型SQL简介

数据库&#xff1a;DataBase&#xff08;DB&#xff09;&#xff0c;是存储和管理数据的仓库数据库管理系统&#xff1a;DataBase Management System&#xff08;DBMS&#xff09;&#xff0c;操作和管理数据库的大型软件。SQL&#xff1a;Structured Query Language&#xff0…
阅读更多...
12.matlab数据分析——多项式的建立 （matlab程序）

12.matlab数据分析——多项式的建立 （matlab程序）

1.简述 多项式及其建立 在运算中我们经常接触到的就是所谓的多项式&#xff0c;比如很常见的一个多项式&#xff1a; 这里我们就说这是一个x的多项式&#xff0c;最高次是2次&#xff0c;常数项是3&#xff0c;二次项的系数是1&#xff0c;一次项的系数是2&#xff0c;相信这些…
阅读更多...
十八、网页端在移动端的像素

十八、网页端在移动端的像素

一、简介 -1. 在不同的屏幕&#xff0c;单位像素的大小是不同的&#xff0c;像素越小&#xff0c;屏幕越清晰。 手机端的像素就是宽度和高度&#xff0c;如iphone6 4.7寸 750 x 1334。 -2. 手机的像素点 远远小于 计算机的像素点。 问题&#xff1a;一个宽度为900px的网页在i…
阅读更多...
【原创】实现ChatGPT中Transformer模型之Encoder-Decoder

【原创】实现ChatGPT中Transformer模型之Encoder-Decoder

作者&#xff1a;黑夜路人 时间&#xff1a;2023年7月 Transformer Block &#xff08;通用块&#xff09;实现 看以上整个链路图&#xff0c;其实我们可以很清晰看到这心其实在Encoder环节里面主要是有几个大环节&#xff0c;每一层主要的核心作用如下&#xff1a; Multi-he…
阅读更多...
Android Glide onlyRetrieveFromCache downloadOnly submit ,kotlin

Android Glide onlyRetrieveFromCache downloadOnly submit ,kotlin

Android Glide onlyRetrieveFromCache downloadOnly submit ,kotlin Glide预加载&#xff0c;加载到磁盘或者内存缓存&#xff0c;然后加载的图片只从缓存&#xff08;磁盘缓存或者内存缓存&#xff09;中取。 private val imageFile File("/storage/emulated/0/DCIM/Ca…
阅读更多...
【无标题】使用html2canvas和jspdf生成的pdf在不同大小的屏幕下文字大小不一样

【无标题】使用html2canvas和jspdf生成的pdf在不同大小的屏幕下文字大小不一样

问题&#xff1a;使用html2canvas和jspdf生成的pdf在不同大小的屏幕下文字大小不一样&#xff0c;在mac下&#xff0c;一切正常&#xff0c;看起来很舒服&#xff0c;但是当我把页面放在扩展屏幕下&#xff08;27寸&#xff09;&#xff0c;再生成一个pdf&#xff0c;虽然排版一…
阅读更多...
.nvmrc无效

.nvmrc无效

背景 既然你已经使用了nvm那么他的功能我就不介绍了。但是使用场景我与开发小伙伴探讨了一下发现很多问题。你的nvm使用方法真的正确吗&#xff1f; 问题&#xff1a;假设现在有10个项目对应10个不同的node版本&#xff0c;你应该怎么来管理呢&#xff1f; 同学1&#xff1a; …
阅读更多...
02 |「新建项目」

02 |「新建项目」

前言 新建项目 文章目录 前言一、步骤二、结构3. Java 文件夹4. res 文件夹5. Gradle Scripts文件 三、运行流程四、Gradle 构建项目1. 是什么2. 作用 一、步骤 1&#xff09;New Project 2&#xff09;Empty Activity 3&#xff09;Finsh 选项&#xff1a; Name&#xff1a…
阅读更多...
在SpringBoot中实现文件上传

在SpringBoot中实现文件上传

1.创建一个SpringBoot的项目&#xff0c;需要导入spring-boot-starter-web的依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-web</artifactId></dependency> 2.编写文件的核心配置applica…
阅读更多...
.NET SqlSuger初次使用

.NET SqlSuger初次使用

文章目录 前言SqlSuger测试DB Fisrt和CodeFirst 前言 我之前在B站上面发视频说如何使用EF框架去生成实体类。我当时做了Mysql,Sql server,Sqlite的适配。但是下面评论区说SqlSuger很好用&#xff0c;而且很多公司都用SqlSuger。 B站视频&#xff1a;C#如何快速开发数据库业务…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023