本文探讨了联合聚类与学习的问题交涉。正如之前的几项研究表明，学习既忠实于要聚类和调整的数据的表示形式到聚类算法可以导致更好的聚类性能，所有的更重要的是，这两项任务是联合执行的。我们在这里提出这样一个方法的k-基于连续重新参数化的方法聚类导致真正联合解决方案的目标函数。的行为我们的方法在各种数据集上进行了说明，显示了其在在对对象进行聚类时学习对象的表示形式。
https://arxiv.org/abs/1806.10069

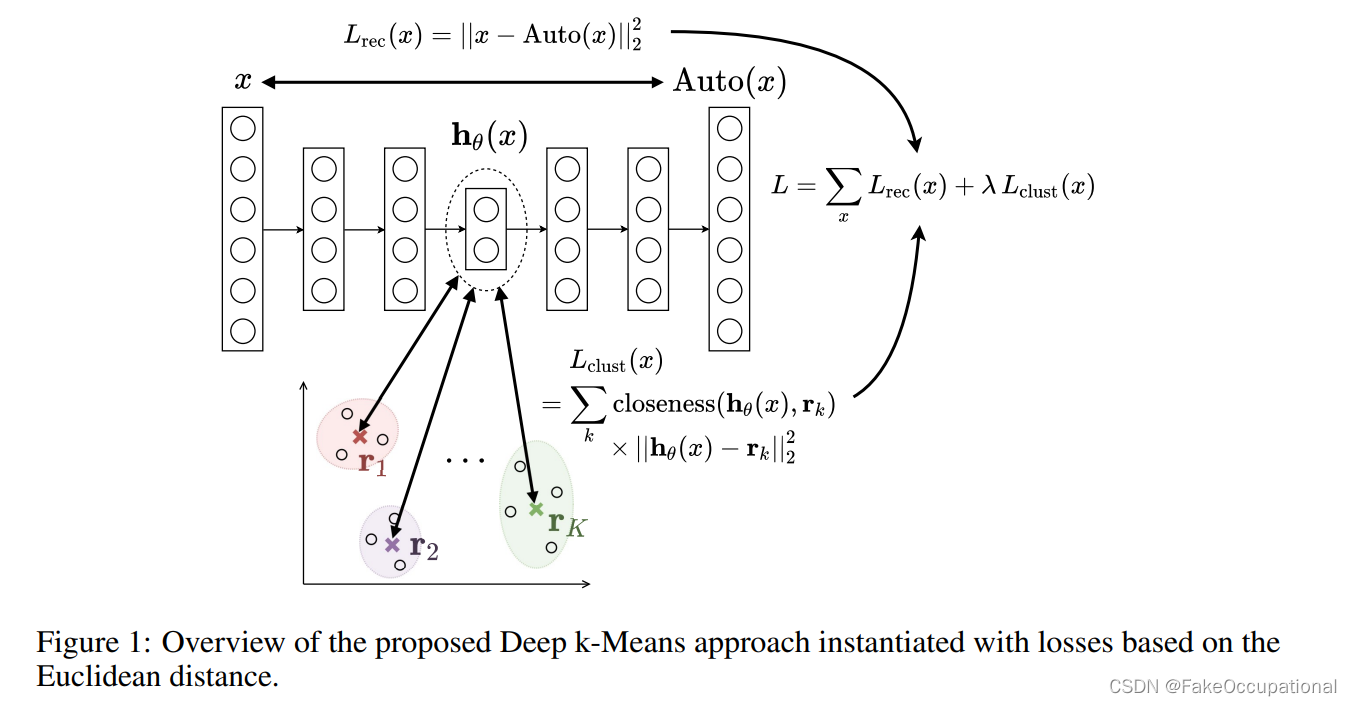
在这里插入图片描述

$x$ ：从需要被聚类的目标集合中采样的样本
$K$ : 聚类中心的个数
$R^p$ ：聚类的映射空间
$R=\{r_1,r_2…，r_K\}$ , $r_i$ 为聚类中心
$\forall y ∈ R^p$ , $c f (y; R)$ 根据度量方式 f 给出 y 最接近的代表表示(gives the closest representative of y according to f).
最终将问题表述如下：
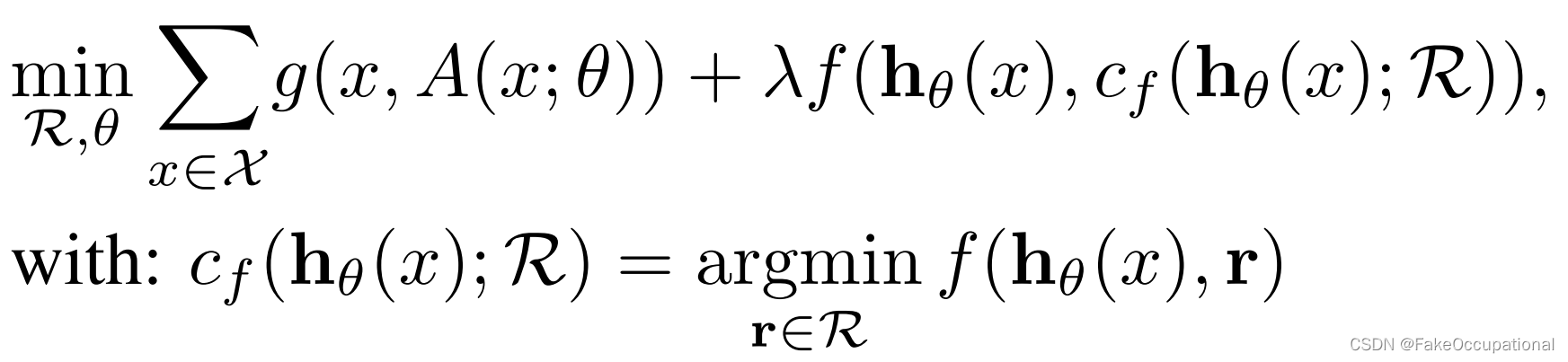
g度量重构损失，f度量聚类损失，上图中两者都为二范数距离

Continuous generalization of Deep k-Means（Deep k-Means 的连续泛化）

现在，我们引入上述问题的参数化版本，它构成了连续泛化，也就是说，这里考虑的所有函数对于引入的参数都是连续的。
我们首先注意到聚类目标函数可以等价为（即只计算最近的聚类中心的距离）：

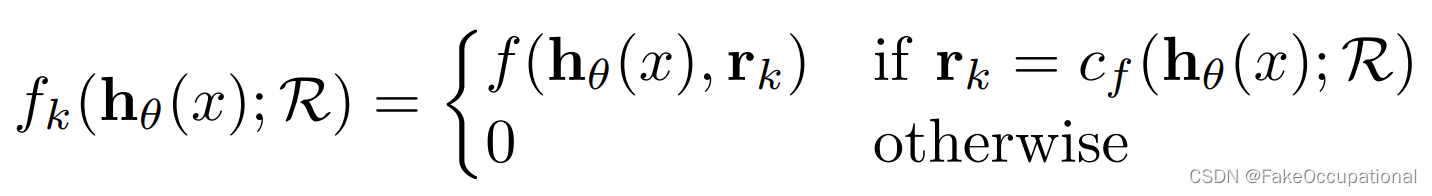
下面作者继续思考了连续化的问题：

假设存在函数 $G_{k,f} (h_θ(x), α; R)$ 满足以下条件：

$G_{k,f} (h_θ(x), α; R)$ 关于 $θ ， R$ 可导，关于 $α$ 连续。关于R可导，指的是关于 $r_i$ 的每一个维度可导。
${ − ∞ , + ∞ } ∃α0 ∈ R ∪ \{−∞, +∞\}$ 使得(类似一个冲击函数):

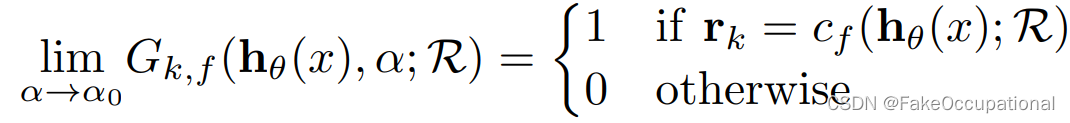
那么，有 $\forall x$ 满足

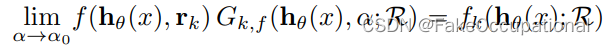
可将初始的损失函数表示为：

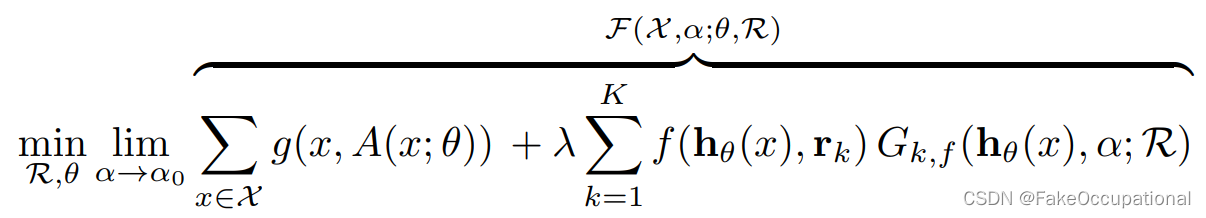
在这里插入图片描述
如此就可以对于一个给定的 α使用以下的梯度下降法进行参数更新了：

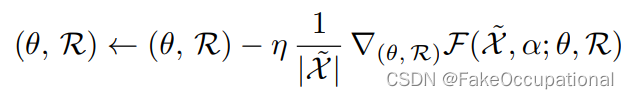
有哪些函数满足以上条件？

$G_{k,f}$ 可以有多种选择。本研究中使用的一个简单选择是基于参数化的 softmax 函数。事实上，softmax 函数可以用作可微分函数argmax 或 argmin 的替代是众所周知的，并且已应用于不同的上下文中，例如最近提出的用于近似分类样本的 Gumbel-softmax 分布[17, 24]。我们采用的参数化softmax函数采用以下形式( $α \in [0, + \infty)$ )：
在这里插入图片描述

Property 3.1略

α的选择

参数α可以用不同的方式定义。事实上，α 可以起到反温度的作用，这样，当 α 为 0 时，嵌入空间中的每个数据点通过 Gk,f 与所有代表都同样接近（对应于完全软分配），而当 α 是+∞，分配是困难的。在第一种情况下，对于深度 k 均值优化问题，所有代表都是相等的，并设置为最小化 Px∈X f(hθ(x), r) 的点 r ∈ Rp。在第二种情况下，解决方案对应于在嵌入空间中精确执行 k-Means，后者是与聚类过程联合学习的。采用确定性退火方法 [28]，可以从较低的 α 值（接近 0）开始，然后逐渐增加它，直到获得足够大的值。首先，代表被随机初始化。由于当α接近0时问题是平滑的，不同的初始化很可能在第一次迭代中导致相同的局部最小值；该局部最小值用于第二次迭代的代表的新值，依此类推。 Gk,f wrt α 的连续性意味着，如果 α 的增量不太重要，则从最初的局部最小值平滑地演化到最后一个局部最小值。在上述确定性退火方案中，α 允许初始化簇代表。自动编码器的初始化也会对获得的结果产生重要影响，之前的研究（例如，[16,31,12,32]）依赖于对此问题的预训练。在这种情况下，可以选择较高的 α 值，以便在预训练后直接获得 k-Means 算法在嵌入空间中的行为。我们在实验中评估这两种方法。

CG

https://github.com/MaziarMF/deep-k-means
对于argmix,argmax这样的算子，如何定义他们对于每个输入变量的导数是问题的难点
论文笔记 Deep k-Means: Jointly clustering with k-Means and learning representations https://blog.csdn.net/2201_75349501/article/details/130308402:与之前([32] B. Yang, X. Fu, N. D. Sidiropoulos, and M. Hong. Towards K-means-friendly Spaces: Simultaneous Deep
Learning and Clustering. In Proceedings of ICML, ICML ’17, pages 3861–3870, 2017.)在连续梯度更新和离散聚类分配步骤之间交替的方法相反，我们在这里表明，可以单独依靠梯度更新来真正联合地学习特征和聚类参数。这最终导致了一种更好的深度k-Means方法，该方法也更具可扩展性，因为它可以充分受益于随机梯度下降（SGD）的效率。此外，我们对不同的方法进行了仔细的比较，方法是（a）依赖于相同的自动编码器，因为自动编码器的选择会影响所获得的结果，（b）在一个小的验证集上调整每个方法的超参数，而不是在没有明确标准的情况下设置它们，以及（c）尽可能强制执行，不同的方法使用相同的初始化和SGD小批量的序列。最后一点对于比较不同的方法至关重要，因为这两个因素起着重要作用，并且每种方法的方差通常不可忽略。

实验中使用的数据集是标准的聚类基准集合。我们考虑了图像和文本数据集，以证明我们的方法的普遍适用性。

图像数据集由MNIST（70000幅图像，28×28像素，10类）和USPS（9298幅图像，16×16像素，10级）组成，这两个数据集都包含手写数字图像。我们将图像重塑为一维向量，并对像素强度水平进行归一化（MNIST在0到1之间，USPS在-1到1之间）。
我们考虑的文本集合是20个新闻组数据集（以下简称20NEWS）和RCV1-v2数据集（下面简称RCV1）。对于20NEWS，我们使用了包含18846个文档的整个数据集，这些文档被标记为20个不同的类。类似于[11]，[28]，我们从完整的RCV1-v2集合中采样了10000个文档的随机子集，每个文档只属于四个最大类中的一个。由于文本数据集的稀疏性，正如Xie等人[28]所提出的，我们选择了具有最高tf idf值的2000个单词来表示每个文档。

在这里插入图片描述