导数与求导

一. 标量向量矩阵的导数

标量，向量，矩阵间求导后的形状：

y\x	标量x(1)	向量 x(n,1)	矩阵 X(n,k)
标量y(1)	(1)	(1,n)	(k,n)
向量 y(m,1)	(m,1)	(m,n)	(m,k,n)
矩阵Y(m,l)	(m,l)	(m,l,n)	(m,l,k,n)

$x和w是向量的情况下：\frac{∂<\bm x ,\bm w>}{∂\bm w} = \bm x^{T}$
$x是矩阵w是向量的情况下：\frac{∂\bm {X w}}{∂\bm w} = \bm X$

$特殊的， s u m 表示求向量元素和时：$

$x是向量的情况下：\frac{∂\bm x.sum}{∂x} = \bm1\space\space其中\bm1是和x同形状的全1向量$

二.Pytorch中的反向求导.backward()

Pytorch中的反向求导用.backward()方法进行实现

y.backward()

x = torch.arange(4.0)
x.requires_grad_(True)
y = torch.tensor([3.0, 1.0, 2.0, 5.0], requires_grad=True)
z = 2 * torch.dot(x, y)
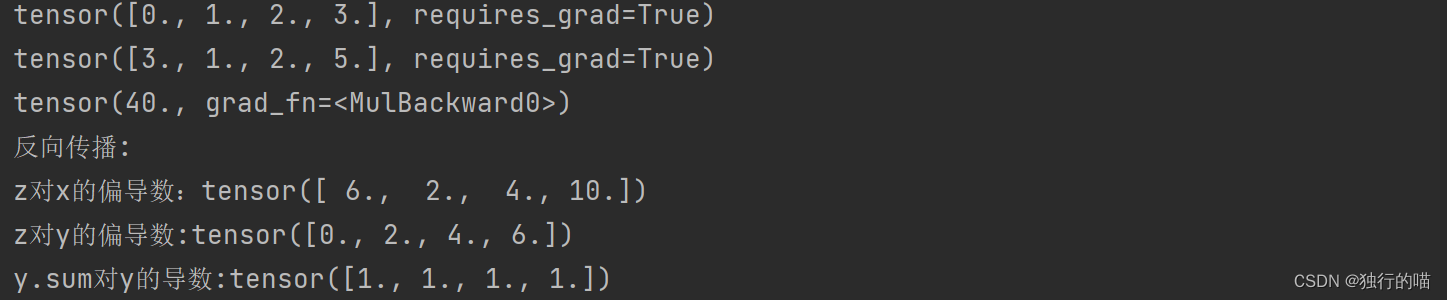
print(x, '\n', y, '\n', z)
print("反向传播:")
z.backward()
print(f"z对x的偏导数：{x.grad}")
print(f"z对y的偏导数:{y.grad}")
y.grad.zero_()
z = y.sum()
z.backward()
print(f"y.sum对y的导数:{y.grad}")

在这里插入图片描述

三.非标量求导

对于向量求导的情况：
在这里插入图片描述
向量y对于向量x的导数是一个雅各比矩阵，在深度学习中通常得到的是一个方阵

假设X = [x1, x2, x3, x4] ; Y = [y1, y2, y3, y4]，其中 ${y_i}={x_i}^2$ ，则Y对于X的导数可表达为雅各比行列式：

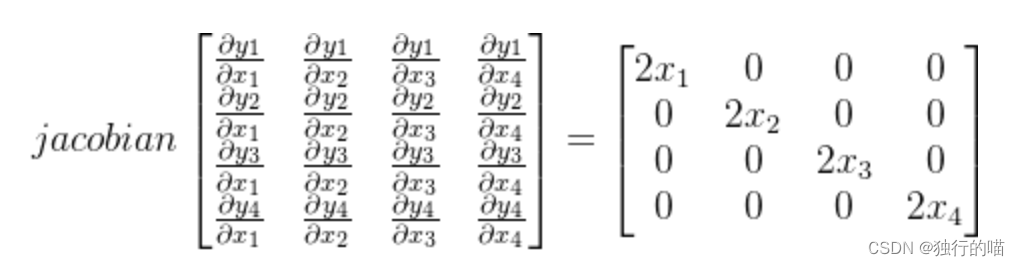
在这里插入图片描述
然而pytorch中backward()方法的输出需要是一个与原张量同维度的张量，所以当遇到向量求导时，必须在backward中额外传入一个参数gradient，gradient是一个与Y同shape的张量，用于左乘雅各比行列式来获得最终与Y同shape形式的导数：

在这里插入图片描述

除了使用传参形式的backward()方法外，还可以使用.sum()方法：

y.sum().backward() #效果等同于y.backward(torch.ones_like(y)

x = torch.tensor([1, 2, 3, 4], requires_grad=True, dtype=float)
y = torch.tensor([3, 4, 5, 6], requires_grad=True, dtype=float)
z = x * y
z.sum().backward()
print(x.grad)

在这里插入图片描述

关于使用.sum()方法求导的数学解释：
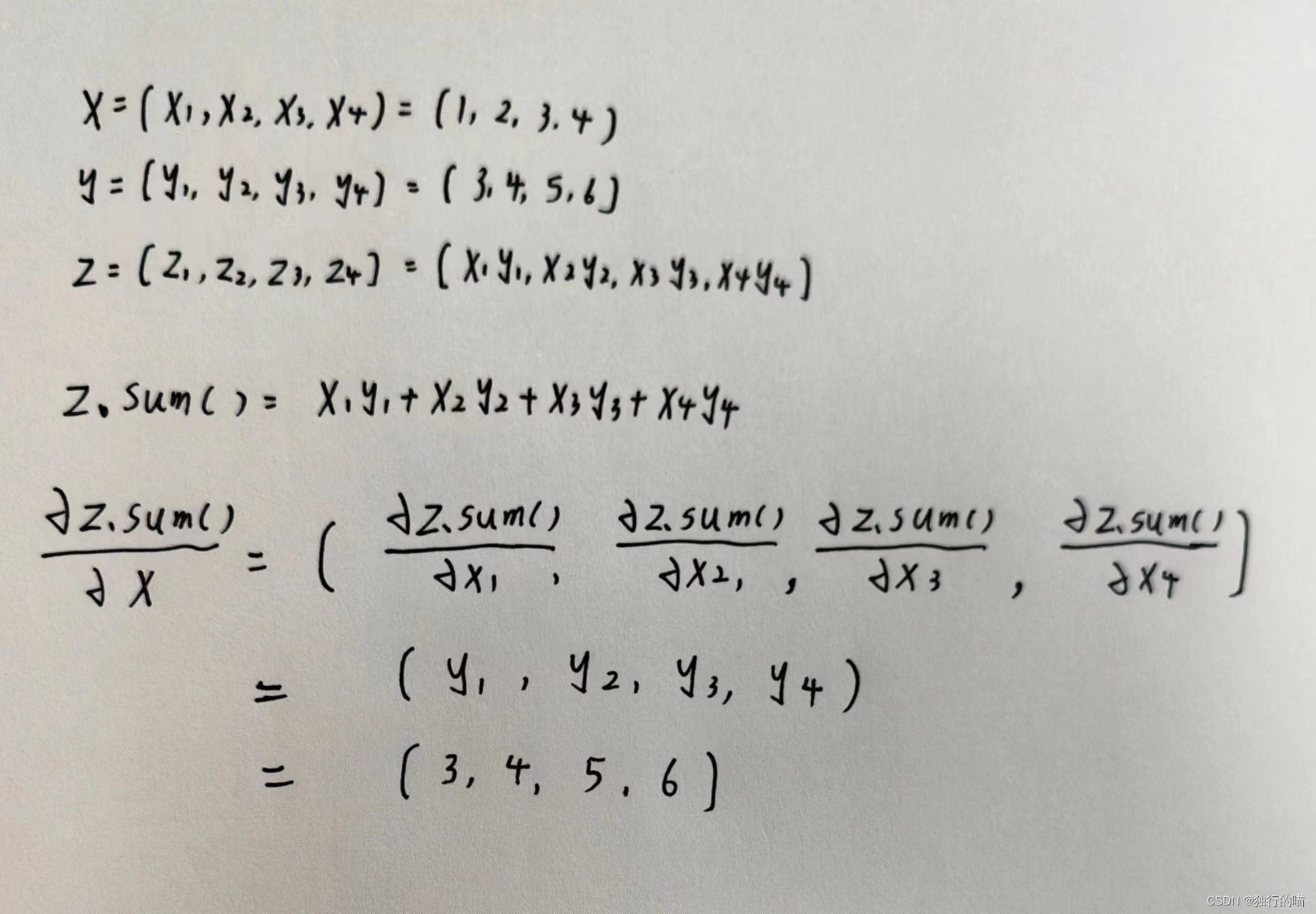
在这里插入图片描述

几种向量求导的代码示例如下：

import torch# 定义向量x和y，同时运算结果z也是向量
x = torch.tensor([1, 2, 3, 4], requires_grad=True, dtype=float)
y = torch.tensor([3, 4, 5, 6], requires_grad=True, dtype=float)
z = x * y
print('z:', z)# 1.对向量z进行反向求导，传入参数为和z同shape的ones向量
z.backward(torch.ones_like(z), retain_graph=True)
print(x.grad)# 2.将参数改为和z同shape的向量[2，3，4，5]后再次反向求导
x.grad.zero_()
z.backward(torch.tensor([2, 3, 4, 5]).reshape(z.shape), retain_graph=True)
print(x.grad)# 3.使用.sum()函数处理向量求导,效果等同于 1：z.backward(torch.ones_like(z)
x.grad.zero_()
z.sum().backward()
print(x.grad)

运行结果：
在这里插入图片描述

使用.sum方法辅助求导后的结果为[3, 4, 5, 6]等效于给所求雅各比行列式左乘了行向量[1, 1, 1, 1]后结果为：[3, 4, 5, 6]
将backward()方法中的参数改为[2, 3, 4, 5]后，相当于给原雅各比行列式左乘了行向量[2, 3, 4, 5]，应该是在原来结果[3, 4, 5, 6]的基础上每行分别乘2，3，4，5，最终结果为[6， 12， 20， 30]